défi pour les 1eres

Bonjour,
Montez que : quelque soit n plus grand ou égal a 2 : ( 1+ 1/2 + ... + 1/n ) n'appartion pas a N.

Bonne chance à tous !

Edit : Ma démonstration n\'est pas très rigide. Il vaut mieux ainsi l\'écraser.

pour te dire, j'ai rien compris des étapes ^^

Tu peux le faire par récurrence d'une autre façons :

Tu suppose que :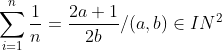


Et tu le prouve par récurrence ..

Puis 2b ne divise pas 2a+1 d'où la conclusion ..

Salam
la recurrence présentée est fausse!!

le faite que (n) 1/i n'appartienne pas à N (suite a l'hypothese)

et que n/(n+1) n'appartienne pas aussi a N

n'impose pas que leurs somme n'appartient pas a N ...

PS lilou khalou tu devrais lacher ce probleme un peu...on t'as presenté maintes solutions avant t'es jamais satisfait

soukki a écrit:

Salam
la recurrence présentée est fausse!!

le faite que (n) 1/i n'appartienne pas à N (suite a l'hypothese)

et que n/(n+1) n'appartienne pas aussi a N

n'impose pas que leurs somme n'appartient pas a N ...

Bien vu !

Je propose cette solution :
Pour n=2 on a

S= 3/2 = (2+1)/2

On suppose que :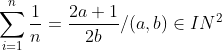


On a :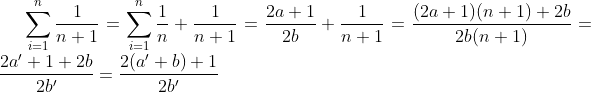




Qui n'appartient pas a IN ..

pourquoi le résultat n'appartient pas a N ?

joli Sylphaen!

lilo, nombre impair/nombre pair === un nombre qui n'appartient pas a N

soukki c'est pas le meme exercice ... celui je vien de le mettre aujourd'hui

il a faut dans la supposition il doit sup^poser que ca n'appartien pas a N pas le contraire

je n'ai pas compris comment il a remplcé sigma par a et b
et pourquoi il a fait entré sigma et a et b pk ne pas se contenter des données ca sera plus facile

stp lilou fais attention avant de dire quoique ce soit puisque c'est ce qu'il a fait ,t'as pas bien vu ,il a ecrit (a,b) appartienne a N

et puis pr te repondre c'est bel et bien le meme exercice , il change seulement de forme

si tu montres que 1+1/2+1/3+.....1/n n'appartient pas a N

alors il existe un m appartenant a N tel que

m< 1+1/2+1/3+.....1/n<m+1

...tu deduis

Sylphaen a écrit:

Je propose cette solution :
Pour n=2 on a

S= 3/2 = (2+1)/2

On suppose que :


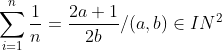
On a :




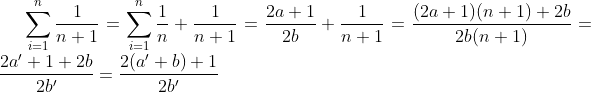
Qui n'appartient pas a IN ..

Salam ...
un nombre ki napratient po a IN nimplike po ke ce nombre =impair sur impair..
mais il implike (dan cet exo car on travaille dans IN) ce nombre=a/b (a et b premiers entre eux)..
donc ta réponse est un peu incomplete car dans cet exo on travaille dans IN donc soi on aura 2a+1/2b oubien 2b/2a+1 mais ce 2eme né po accepté car A=1+1/2+..+1/n car n>=2 donc on a toujour un nombre kyé pair flma9am
si tu signale cela ta réponse cera correcte...

Oui et j'ai oublié le cas où n+1 et paire

tu pourra poster ta reponse détaillée car j'ai encore du mal a comprendre comment t'a remplacé a et b etc ...

merci d'avance

salam....
la solution de sylphaen n'est pas incomplète mais plutôt incorrecte....car depuis le debut le raisonnement est faux...en effet....A n'appartient pas à IN n'équivaut pas à A=impair/pair je peux donner comme contre exemple A=2/3
l'implication A=impair/pair===>A n'appartient pas à IN est vraie mais la réciproque non...
ma solution(sauf erreur)....
récurrence:
pour n=2 la propriété est vraie....
supposons que c'est vrai pour n....on a donc :

(avec S est rationnel puisque c'est une somme de nombres rationnels)
démontrons que c vrai pour n+1....
raisonnement par absurde ...supposons que :

alors b(n+1) / an+a+b
==>b(n+1)/b(an+a+b)-ab(n+1)
<=>b(n+1)/b²<=>n+1 / b <=>k(n+1)=b (1)(avec k£IN)<=>1/n+1=k/b
on a donc S_{n+1)=a/b+k/b £IN
alors : b / a+k<=>b / a(n+1)+k(n+1)
<=> b / a(n+1)+b==> b / a (n+1)
or pgcd(a,b)=1 alors b / n+1 et de (1) on a : n+1 / b
alors n+1=b
on a S_{n+1)=a/b+1/(n+1)=(a+1)/(n+1) appartient à IN alors n+1 / a+1
=>n+1 / n(a+1)-n-1=na-1
n+1/ a(n+1)+an-1=a-1
alors n+1 / a+1-(a-1)=2 alors n+1 / 2 alors n=1 ce qui est absurde
conclure......
P.S. / :divise

majdouline a écrit:

salam....
la solution de sylphaen n'est pas incomplète mais plutôt incorrecte....car depuis le debut le raisonnement est faux...en effet....A n'appartient pas à IN n'équivaut pas à A=impair/pair je peux donner comme contre exemple A=2/3
l'implication A=impair/pair===>A n'appartient pas à IN est vraie mais la réciproque non...

C'est plutôt A=3/2 xD

Voici ce que je propose ..
Pour n=2 on a

S= 3/2 = (2+1)/2

On suppose que : avec 2a+1 ^ 2b =1 ( pgcd ..)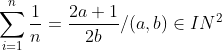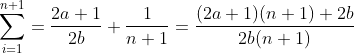


Si n+1 est impaire alors le nominateur est impaire ..
maintenant si n+1 est paire donc :
∃ (p ,s) £ IN x 2IN +{1} : n+1= 2^p X s
∃ (p' ,s') £ IN x 2IN +{1} : b=2^p' X s'
On aura donc :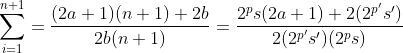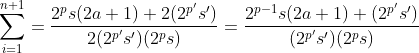



Si p-1<= p' on aura :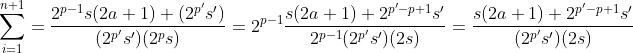


Qui est impaire/paire ..
On fait de même pour l'autre cas ..
Sauf erreur bien sûr :d

Sylphaen a écrit:

majdouline a écrit:

salam....
la solution de sylphaen n'est pas incomplète mais plutôt incorrecte....car depuis le debut le raisonnement est faux...en effet....A n'appartient pas à IN n'équivaut pas à A=impair/pair je peux donner comme contre exemple A=2/3
l'implication A=impair/pair===>A n'appartient pas à IN est vraie mais la réciproque non...

C'est plutôt A=3/2 xD

je parle pas de notre somme mais je parle d'un A quelconque.....

en tt cas je crois maintenant que ce raisonnement est correct:
car ici la récurrence ne se base pas sur démontrer que : (∀n£IN) S_{n}pas entier mais de:
(∀n£IN)(∃(a,b)£IN²) tel que S=(2a+1)/b ce qui implique que (∀n£IN) S_{n}pas entier...et c'est ce que je voulais que tu indique dans cette solution...car d'après ce que tu as écrit t'as pas indiqué la propriété qu'on veut démontrer par récurrence....
mais bon........ voici un lien:
http://www.mathramz.com/xyz/viewtopic.php?f=4&t=3236&p=24254&hilit=http%3A%2F%2Fwww.mathramz.com%2Fxyz%2Flatexrender%2Fpictures%2F197c90a4a2507c44d5818c06a75db0c8.png#p24254

Oui j'avais mal rédigé ..En effet c'est
∀ n£IN*-{1} ∃(a;b)£IN*² : S=2a+1/b
pas
(∀n£IN)(∃(a,b)£IN²) : S=2a+1/b

^^