elfenlied
Débutant
 Nombre de messages : 1
Age : 32
Localisation : Kénitra
Date d'inscription : 27/10/2008
 | | Sujet: inégalité Jeu 04 Fév 2010, 12:21 | |
| soient a,b,c >0 et n de N* montrer que : a^n/(b+c) + b^n/(c+a) + c^n/(a+b) >= [a^(n-1)+b^(n-1)+c^(n-1)]/2 bonne chance inegalita 9wiya ^^ pour ceux qui ont été dans le stage olympiad je suis Seif de kénitra^^ c'est mon premier post  INTAHA !!! | |
|
majdouline
Expert sup
 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: inégalité Jeu 04 Fév 2010, 12:36 | |
| par Chebyshev on a : (\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b})}{3}) par Cauchy Schwartz on a : }) alors : }{2(a+b+c)}) (1) encore par Chebyshev on a : (a^{n-1}+b^{n-1}+c^{n-1})}{3}) (2) et (1) et (2) on a: 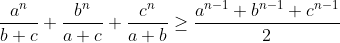 CQFD.... P.S.bienvenue sur le forum | |
|
tarask
Expert sup
Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
| | Sujet: Re: inégalité Lun 21 Juin 2010, 12:44 | |
| je suis un peu en retard , mais est-ce-qu'on po faire le raisonnement par reccurence ?  | |
|
master
Maître
Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
| | Sujet: Re: inégalité Lun 21 Juin 2010, 15:01 | |
| mmm , je crois que tu peux !
pour n=1 ==> (a/b+c ) + (b/c+a) + (c/a+b) >= 3/2
ce qui est vrais !!
donc supposons que l'inégo est vrais pour n !
pour n+1 :
il fallait prouver que : (a^(n+1)/b+c)+(b^(n+1)/a+c)+(c^
(n+1)/a+b) >= a^n+b^n+c^n/2
ce qui est facile a le prouver ! ^^ | |
|
tarask
Expert sup
Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
| | Sujet: Re: inégalité Lun 21 Juin 2010, 15:20 | |
| oui c'est ce que j'allais ecrire hhh pk quand g vu le fameux "n" jme suis dis qu'on pourra faire par recurrence :p merci Master | |
|
