Equation de haut niveau:

Résolvez en IR:
(E):3x^8-4x^6+8x^4-4x^2+3=0.
Bonne chance.

indice :

remarquer que "0" n'est pas une solution et diviser par x^4

On pose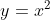
L'équation devient :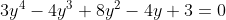
y étant positif, l'équation se doit d'être résolu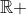
D'après l'IAG, l'on a :


En sommant, il vient que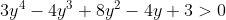
L'équation n'a donc pas de solution.

Oui, l'équation n'a pas de solution.
Pour notre niveau, il faut utiliser le discriminent.
Merci pour la réponse.
Après, je vais rédiger la solution complète.

Voici la solution complète de cette équation:
On a 3*0^8-4*0^6+8*0^4-4*0^2+3=3.
Donc 0 n'est pas une solution.
Lorsqu'on divise par x^4 on obtient l'équation équivalente:
(E'):3x^4-4x^2+8-4/x^2+3/x^4=0.
Posons t=x^2+1/x^2 avec t>0.
Et donc (t^2)-2=x^4+1/x^4.
L'équation (E') elle aussi équivaut (E''):3t^2-4t+2=0.
Léquation E'' n'a pas de solution car son discriminent est négatif:
# [16-4*(-2)*(-3)]=(16-24)=-8 #.
Finalement léquation (E) n'a pas de solution dans IR.

Voici une autre équation qu'il faut résoudre en Q:
(5x-y+6)V2 +x-7y+5=0.
Bonne chance.

nmo a écrit:

Voici une autre équation qu'il faut résoudre en Q:
(5x-y+6)V2 +x-7y+5=0.
Bonne chance.

Voici ma réponse:
On remarque que V2 n'appartient pas à Q.
Donc 5x-y+6=0.
Il s'ensuit que x-7y+5=0.
Il faut résoudre le système suivant en Q:
5x-y+6=0.
x-7y+5=0.
Je vais procéder par substition:
De la deuxième équation, on tire x: x=7y-5.
Et on le remplace dans la deuxième équation: 5(7y-5)-y+6=0.
Donc 35y-25-y+6=0.
Donc 34y-19=0.
Donc 34y=19.
Finalement y=19/34.
Et puisque x=7y-5.
On trouve x=37/34.
La solution de cette équation en Q est S={37/34,19/34}
Sauf faute de calcul.

Voici une autre équation assez difficile:
Résolvez en IR l'équation:
4^x+3*2^x=88.
Bonne chance.

Pose a=2^x ,
L'équation équivaut à :
a²+3a-88=0
Dt=361

a=-11 ou a=8
Donc :
2^x=-11(imp) ou 2^x=8

x=3

S={3}

Très bonne méthode sylphaen.
C'est juste.

Cette fois un défi:
Résolvez en IR l'équation suivante:
(x+2)(x+4)(x-6)(x-8 )=2925.
Bonne chance.

Posons
a=x-2
Eq <=>
(a+6)(a+4)(a-6)(a-4)=2925
(a²-16)(a²-36)=2925
a^4 -52a²+576=2925
a^4-52a²-2349=0
Eq <=>
Puis b=a²
b²-52b-2349=0
Dt=12100 / Vdt=110
b=-29 ou b=81
Donc :
a²=81 <=> a=9 ou a=-9
Et :
x-2=9 ou x-2=-9
x=11 ou x=-7
S={-7,11}
Sauf erreur ..

C'est vrai sylphaen. Très bonne méthode.

De retour avec un autre exercice:
Résolvez en IR l'équation:
x^5+2x^4+4x^3+8x^2+16x+32=0.
Bonne chance.

nmo a écrit:

De retour avec un autre exercice:
Résolvez en IR l'équation:
x^5+2x^4+4x^3+8x^2+16x+32=0.
Bonne chance.

étant strictement positif, l'équation se réduit à :
Les solutions réelles de l'équation sont : -2.

C'est juste Dijkschneier.
Voici une autre méthode:
On remarque que 2 n'est pas une solution.
Donc x#2.
Donc x-2#0.
Donc (x-2)(x^5+2x^4+4x^3+8x^2+16x+32)=0*(x-2).
Donc x^6-2^6=0. (après la simplification).
Donc x^6=2^6.
Donc x=-2 car 2 ne réalise pas l'équation.

Soit a un réel vérifiant x^3+1/x^3=18.
Calculez x^4+1/x^4.
Bonne chance.

Je réponds moi-même:
Posons t=x+1/x.
Donc t^2=x^2+2+1/x^2.
Donc t^2-2=x^2+1/x^2.
Donc (x^2+1/x^2)(x+1/x)=(t^2-2)t.
Donc x^3+x+1/x+1/x^3=t^3-2t.
Donc x^3+t+1/x^3=t^3-2t.
Donc x^3+1/x^3=t^3-3t.
Donc 18=t^3-3t.
Soit en résumé t^3-3t-18=0.
On remarque que 3 est solution évidente.
On factorise avec 3 pour obtenir (t-3)(t^2+3t+6)=0.
Donc t-3=0 ou t^2+3t+6=0.
Pour t-3=0 on obtient t=3.
Pour t^2+3t+6=0 c'est impossible car son discriminent est négatif
(3^2-4*6=9-24=-13).
D'autre part on a x+1/x=3.
Donc (x+1/x)^2=3^2.
Donc x^2+2+1/x^2=9.
Donc x^2+1/x^2=7.
Donc (x^2+1/x^2)^2=7^2.
Donc x^4+2+1/x^4=49.
Finalement x^4+1/x^4=47.

L'ultime équation:
Considérons l'équation (E): x²+5y²=6xy.
Sachant que y#0 et x#y.
1-Calculez x/y.
2-Trouvez tous les nombres x et y appartenant à N et inférieur à 10 et et qui sont des solutions pour l'équation (E).
Bonne chance

Pour cette équation:
Premièrement:
On a x²+5y²=6xy.
Donc, en divisant par xy x²/xy+5y²/xy=6xy/xy.
Donc x/y+5y/x=6.
Posons x/y=k.
L'équation devient k+5/k=6.
Donc k²+5k=6.
Donc k²+5k-6=0.
Cet équation a pour discriminent 49. (5^2-4*1*(-6)=25+24=49)
D'ou les deux solutions k=1 ou k=-6.
Donc x/y=1 ou x/y=-6.
Et puisque x#y.
Il s'ensuit que x/y#1.
Donc x/y=-6.
Deuxièmement:
On a x et y appartiennent à N.
Donc leur quotient est positif.
Donc il n'existe aucun couple d'entiers naturels vérifiants l'équation (E).
Sauf faute de calcul.