the kiler
Maître
 Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
 | | Sujet: jli probleme Ven 26 Fév 2010, 12:10 | |
| determiner tous les triplets des nombres réels tel que:  | |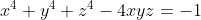
|
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: jli probleme Ven 26 Fév 2010, 12:28 | |
| L'inégalité arithmético-géométrique déclame que : 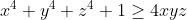 , avec égalité ssi x=y=z. Ainsi, l'équation devient : 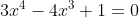 L'unique solution réelle à cette équation est 1. Le seul couple de solutions est donc (1,1,1). | |
|
the kiler
Maître
Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
| | Sujet: Re: jli probleme Ven 26 Fév 2010, 13:03 | |
| nn dijjkschneier.x y et z ne sont pas des réels positifs | |
|
the kiler
Maître
Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
| | Sujet: Re: jli probleme Ven 26 Fév 2010, 13:05 | |
| | |
|
the kiler
Maître
Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
| | Sujet: Re: jli probleme Ven 26 Fév 2010, 14:44 | |
| l'egalité est equivalent : ^{2}+\left ( z^{2}-1 \right )^{2}+2\left ( xy-z \right )^{2}=0\Leftrightarrow \left ( x^{2}=y^{2} \right...et...z^{2}=1...et..xy=z )\Leftrightarrow S=\left \{ \left ( 1,1,1 \right ),\left ( -1,-1,1 \right ),\left ( -1,1,-1 \right ),\left ( 1,-1,-1 \right ) \right \}) | |
|
