L'olympiade de Settat: (deuxième étape)

Slt Mr Sylphaen

Sylphaen a écrit:

Bon voici une autre :
on a clairement :

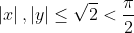
Si |x|>|y| donc :

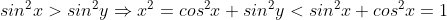
Donc :
1>|x|>|y| cad x²+y²<2 absurde ..
même raisonnement pour |y|>|x|
Donc |x|=|y| => |x|=|y|=1

Votre solution est moin cher, j'ai trop aimé votre méthode.Les solutions que t'as trouvé paraientt clairement juste.

[quote="Sylphaen"]Pour le 2 c'est m=3 et p=2
Posons :
quote]

x se trouve dans l'ensenble rationel non ? car V3/V2 ou V3 apartient à Q.

mon frere dijkschneir tu as raison pour l ex3 mais on ne peux ni comprendre ni l ecrir car pour ce niveau on n a pas encore etudier tout ca.mais vraiment tu est expert

sniperb a écrit:

mon frere dijkschneir tu as raison pour l ex3 mais on ne peux ni comprendre ni l ecrir car pour ce niveau on n a pas encore etudier tout ca.mais vraiment tu est expert

On ne peut pas l'écrire car la durée du test qu'on a passé ne le permet pas.

nmo a écrit:

Ta solution M.Marjani pour le troisième est fausse.
Essaye autrement.

Non je pense pas

A=1,A=-1,B=1,B=-1

Donc : les solutions : (1,-1) ou (1,1) ou (-1,1) ou (-1,-1)

J'ai fais une autre methode, mais la methode de Sylophean reste la meilleure.

Dijkshneier a écrit:

Sylphaen a écrit:

Pour le 2 c'est m=3 et p=2
Posons :

Donc :



Donc :
pm=6
avec une disjonction de cas sur IN on trouve finalement p=2 et m=3
..
Sauf erreur ..

x est supposé appartenir à l'ensemble des rationnels, plutôt qu'à l'ensemble des naturels.

Oui mais bon ca donne le même résultat ^^

Je termine la démonstration de sylphaen:
On veut déterminer m et p pour que (V2+Vm)/(V3+Vp) soit rationel.
Puisque m et p sont des naturels, et les diviseurs de 6 sont 1, 2, 3, et 6.
Il s'ensuit que p=1 et m=6 ou p=6 et m=1 ou p=2 et m=3 ou p=3 et m=2.
Le premier cas: p=1 et m=6.
On a x=(V2+Vm)/(V3+Vp)=(V2+V6)/(V3+V1)=(V2)(V1+V3)/(V3+V1)=(V2).
Donc c'est faux car V2 n'est pas rationel.
Le second cas: p=6 et m=1.
On a x=(V2+Vm)/(V3+Vp)=(V2+V1)/(V3+V6)=(V2+V1)/(V3)(V1+V2)=1/(V3).
Donc c'est faux car 1/V3 n'est pas rationel.
Le troisième cas: p=2 et m=3.
On a x=(V2+Vm)/(V3+Vp)=(V2+V3)/(V3+V2)=1.
Donc c'est juste car 1 est rationel.
Le quatrième cas: p=3 et m=2.
On a x=(V2+Vm)/(V3+Vp)=(V2+V2)/(V3+V3)=2(V2)/2(V3)=(V2)/(V3).
Donc c'est faux car V2/V3 n'est pas rationel.
On conclut que pour que le nombre (V2+Vm)/(V3+Vp) soit rationel, il faut que m=3 et p=2.

Pour le dernier, voici ce que j'ai fait:
Soit O le centre de ce cercle et I, J, K, et L les projetés orthogonals respectifs de O sur les droites (AB), (BC), (CD), et (DA).
On a O est un point à l'interieur de l'angle IBJ.
Et on a (OI) et (OJ) sont perpendiculaires sur (AB) et (BC) les deux côtés de l'angle IBJ.
Et on a OI=OJ car (OI) et (OJ) sont deux rayons dans le même cercle.
Donc [BO) est la bissectrice de l'angle IBJ.
Donc IBO=OBJ. (angles) ==>(a)
Et on a (OI) une droite perpendiculaire sur la droite (AB).
Donc OIB=90°. (angle) ==>(1)
Et on a (OJ) une droite perpendiculaire sur la droite (BC).
Donc OJB=90°. (angle) ==>(2)
On sait que la sommes des mesures des trois angles d'un triangle vaut 180°.
Donc, on a dans le triangle IBO: IBO+BOI+OIB=180°. (angles)
Et on a dans le triangle BOJ: BOJ+BJO+OBJ=180°. (angles)
Donc IBO+BOI+OIB=BOJ+BJO+OBJ. (angles)
Donc, en utilisant 1 et 2 et a il vient que JOB=BOI. (angles) ==>(b)
Et on a (OB) un côté commun des deux triangles IBO et BOJ.
Donc, en utilisant a et b il vient que les deux triangles IBO et BOJ sont isométriques.
Donc les mesures de leurs côtés juxtaposés sont égaux.
Donc IB=BJ.
De même JC=CK.
De même KD=DL.
De même LA=AI.
Soit P le périmètre de ce trapèze.
On a P=AB+BC+CD+DA.
Donc P=AB+(BJ+JC)+CD+(DL+LA).
Donc P=AB+CD+BJ+AL+JC+DL.
Donc P=AB+CD+(BI+AI)+(CK+DK).
Donc P=AB+CD+AB+CD.
Donc P=84+25+84+25.
Donc P=218.
Sauf faute de frappe.

Pour le 3ème exo , la solution proposée par sylpha est simple mais je n'arrive pas a trouver la déduction qu'il a utilisé en premier ( on a clairement ... ) si je peux etre éclairé par rapport a ca ca serait gentil

3ème exercice je suis pas sur


On a
Sin^2a+con^2B=B^2
Sin^2B+cOs^2a=A^2


alors
A^2+B^2=Sin^2a+con^2B+Sin^2B+cOs^2a
A^2+B^2=2



On a
Sin^2a+con^2B=B^2
Sin^2B+cOs^2a=A^2

alors
Sin^2a+con^2B=B^2
-Sin^2B-cOs^2a=-A^2
alors
B^2-A^2=Sin^2a+con^2B-Sin^2B-cOs^2a

puisque Sin^2a=1-cos^2a
et Sin^2B=1-Cos^2B
alors

B^2-A^2=Sin^2a+con^2B -1-1+cos^2B+sin^2a
B^2-A^2=2-2=0

de
B^2-A^2=0
on conclut que
B^2=A^2
donc
A^2+B^2=2
deviens
A^2+A^2=2
2A^2=2
Donc
A=1 ou A=1 B=1 ou B=-1
et puisque -1 n'appartient pas à R^2
alors
A=1 et B=1

pain-aymen a écrit:

puisque Sin^2a=1-cos^2a
et Sin^2B=1-Cos^2B
alors
B^2-A^2=Sin^2a+con^2B -1-1+cos^2B+sin^2a
B^2-A^2=2-2=0
de
B^2-A^2=0
on conclut que
B^2=A^2
donc
A^2+B^2=2

Je trouve que ce qui est en rouge est faux ou mal démontré , surtout la premiere que je n'arrive pas a comprendre ...

pain-aymen ; la meme remarque !! j'ai pas compriis !!!

pain-aymen a écrit:

3ème exercice je suis pas sur


On a
Sin^2a+con^2B=B^2
Sin^2B+cOs^2a=A^2


alors
A^2+B^2=Sin^2a+con^2B+Sin^2B+cOs^2a
A^2+B^2=2



On a
Sin^2a+con^2B=B^2
Sin^2B+cOs^2a=A^2

alors
Sin^2a+con^2B=B^2
-Sin^2B-cOs^2a=-A^2
alors
B^2-A^2=Sin^2a+con^2B-Sin^2B-cOs^2a

puisque Sin^2a=1-cos^2a
et Sin^2B=1-Cos^2B
alors

B^2-A^2=Sin^2a+con^2B -1-1+cos^2B+sin^2a
B^2-A^2=2-2=0

de
B^2-A^2=0
on conclut que
B^2=A^2
donc
A^2+B^2=2
deviens
A^2+A^2=2
2A^2=2
Donc
A=1 ou A=1 B=1 ou B=-1
et puisque -1 n'appartient pas à R^2
alors
A=1 et B=1

Nice, Nice man
C'est la methode que j'ai voulu posté aprés Mr Sylphaen, mais sa methode reste 'verry good'.
Bonne chance.

dsl cé vrai qu'il y a un petit truc que j'ai oublié mais je l'ai déjà noté hier, je corrigerais dès mon retour de l'olymp

pain-aymen a écrit:

dsl cé vrai qu'il y a un petit truc que j'ai oublié mais je l'ai déjà noté hier, je corrigerais dès mon retour de l'olymp

là: B^2-A^2=0 , A²+B²=2
Tu peux déduire.. Sans continuer de remplacer.
=> B^2=A^2 <=> |B|=|A| .. et: A²+B²=2.
D'ou S={(1,1),(-1,-1),(1,-1),(-1,1)}

Bonne chance.

Bonjour tout le monde,
Pour l exercice 3 jé trouvé ke vos solutions étaient incompletes ou plutot mal justifiés .
Et jé trouvé une solution plutot complete :
On a va noter : A = alpha et B = Beta
On a Sin(A)^2 + Cos(B)^2 = B^2 «= (1)
Et Sin(B)^2 + Cos(A)^2 = A^2 «= (2)

Donc de (1) et (2), On conclut que A^2 + B^2 = 2
A ce stage la, deux cas se présenent soit
A = B , ou bien A différent de B
1. Voir si A est différent de B.
Premierement si A est différent de B
Alors Sin(A) est différent de Sin(B)
Sauf une seule condition é ke A = B +(pi\2)
Dans ce cas ci : Sin(A)^2 = Cos(B)^2
Et Sin(B)^2 = Cos (A)^2
Ce qui donne Sin(B) = B\V2 Et Cos (B) = B\V2
Donc Sin(B) = Cos(B) Et meme chose pour A
Donc A=B = pi\4 + k(pi\2) \ k £ Z

Et ce résultat ne vérifie pas les équations.
Donc (Sin(A)^2 est différent de Sin(B)^2) «= (1)

Et si A est différent de B
Alors Cos(A)^2 est différent de Cos(B)^2
Sauf si A = -B
Ce qui donne A = 1 ou A = -1
Et B = 1 ou B = -1
Et donc cela est faux.
Donc (Cos(A)^2 est différent de Cos(B)^2 ) «= (2)
De (1) et de (2) on peut conclure que
Cos(B)^2 + Sin(B)^2 est différent de Cos(A)^2 + Cos(B)^2

Or cela é faux puisque Cos(A)^2 + Sin(A)^2 = Cos(B)^2 + Sin(B)^2 = 1

Et donc le fait que A est différent de B é faux.
Donc A = B
On a A^2 + B^2 = 2
Donc A = 1 ou A =-1
et B = 1 ou B = -1

Donc,
S = ( (1;1);(1;-1);(-1;1);(-1;-1) )
Désolé de la longeur mais au moins cé complet
J espere ke jé été clair
Les solutions ke vs avez présenté sans juste et je respecte votre avis mais pour moi ca manque de justification

Mehdi, éleve du TC