| | L'olympiade de settat: (troisième étape) |  |
|
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: L'olympiade de settat: (troisième étape) Sujet: L'olympiade de settat: (troisième étape)  Ven 21 Mai 2010, 18:17 Ven 21 Mai 2010, 18:17 | |
| Exercice 1:Soit a un entier. Ecrivez 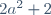 sous la forme de la somme de deux carrés parfaits. Exercice 2:a est un réel non nul. Considérons les deux équations: : x^2-(2a+1)x+a=0) . Et : x^2+(a-4)x+a-1=0) . Précisez le nombre a sachant que: *l'équation ) admet deux racines 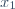 et 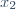 . *l'équation ) admet deux racines 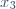 et 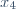 . * }{a}) . Exercice 3:1-Précisez une valeur maximale pour la fonction numérique =x^2-x^4) . 2-Soit (C) un cercle de centre O et de diagonale [AC]. K est un point se variant de [OB]. La droite passant de K et parallèle à (AC) coupe le cercle (C) en deux points M et N. Précisez OK pour que la surface du triangle OMN soit maximale. Exercice 4:Montrez que: \cos{\frac{\pi}{8}}+\sin{\frac{\pi}{8}}=0) .
Dernière édition par nmo le Ven 10 Déc 2010, 10:32, édité 2 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Ven 21 Mai 2010, 18:22 Ven 21 Mai 2010, 18:22 | |
| Les deux exercices qui sont difficiles sont le 2 de la question 3 et le dernier.
Je vous invite à partager avec moi vos réponse afin de vérifier mes résultat.
Bonne chance.
P.S: Ne voyez-vous pas que le premier exercice est trivial et ne doit pas être dans ce test?
Pour le deuxième, on applique les égalités du cours. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Ven 21 Mai 2010, 18:43 Ven 21 Mai 2010, 18:43 | |
| Pour le dernier :
On prend un triangle ABC tq
<A=3pi/4
<B=<C=pi/8
Appliquer Alkashi pour avoir :
BC²=(2+V2)AB²
Ensuite on a : cos(pi/ 8 ) =BC/2AB ..
Trouver cos(pi/8 ) et sin(pi/8 )puis vous trouvez l'égalité demandée .. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Ven 21 Mai 2010, 21:28 Ven 21 Mai 2010, 21:28 | |
| Bonjour Mr nmo, je pense que l'olymp était plus façile que d'habitudes. Je pense que t'as bien travaillé  1/ a²+1+a²+1=a²+2a+1 +a²-2a+1=(a+1)²+(a-1)² EX2: 2/**)Delta=(2a+1)²-4a=4a²+1>0 Donc tout a de |R vérifiant l'énoncé. **)Delta=(a-4)²-4(a-1)=a²-12a+20 Delta2= 144-80=64>0 Donc tout réel a vérifiant l'énoncé. **)a=(x1x2x3x4)²/(x1x4+x2x3) x1=(2a-V(4a²+1))/2 et: x2=(2a+V(4a²+1))/2 x3=-(a+4)/2 et: x4=(12-a)2 Donc calcul.. EX3: Petite figure:  1/ f(x)=x²-x^4 <=> f(x)-x²=-x^4 x^4>=0 <=> -x^4=<0 => f(x)-x²=<0 <=> f(x)=<x² Donc x² est une valeur maximal pour f(x). 2/ Soit f(x) la surface du triangle OMN. S amn=(1/2)*OM*ON*Cos{MON}=(1/2)*OM²*Sin(MON) (OM=r=cte)=> f(x)=(1/2)*r²*Sin(MON)=(1/2)*r²*x Donc il faut que x soit maximal pour que la surface soit maximal. Donc: x=Sin{MON}=1=Sin(Pi/2) [car: -1=<sinx=<1 ça veut dire qu'il faut que le triangle OMN soit rectangle en O pour que ça surface soit maximale. => On a: OK (واسط) [MN] et passant par O. Et: OMN=ONM Donc: OMC est un trangle rectangle et issoecle en O. => OK=(1/2)MN (علاقة مترية). EX4: J'avais l'idée de partir dans une démonstration déjà faite sur Pi/8.. la méme idée de Mr Sylphaen, donc je vais changer de methode: On a: +Sin(\frac{\Pi}{8})=\sqrt{2}*Cos(\frac{\Pi}{8})) Multipliant chaque fois soit par Sin(Pi/  soit pas Cos(Pi/  : +Cos(\frac{\Pi}{8})*Cos(\frac{\Pi}{8})=\sqrt{2}Cos^2(\frac{\Pi}{8})) *Sin()+Sin^2(\frac{\Pi}{8} )=\sqrt{2}Cos(\frac{\Pi}{8} )*Sin(\frac{\Pi}{8} )) *Sin(\frac{\Pi}{8})=(\sqrt{2}+1)(Sin^2(\frac{\Pi}{8})) & \\ Cos(\frac{\Pi}{8})*Sin(\frac{\Pi}{8})=(\sqrt{2-1)}(Cos(\frac{\Pi}{8})) & \end{Bmatrix}) =\frac{2-\sqrt{2}}{4}\Leftrightarrow Sin(\frac{\Pi}{8})=\frac{\sqrt{2-\sqrt{2}}}{2}) Cos(Pi/ Cos(Pi/ et Sin(Pi/ et Sin(Pi/ £ [0,Pi/2] £ [0,Pi/2]+Cos^2(\frac{\Pi}{8})=1\Leftrightarrow Cos(\frac{\Pi}{8})=\frac{\sqrt{2+\sqrt{2}}}{2}) Dans l'equation on remplace Cos(Pi/huit) et Sin(Pi/Huit) par leurs valeurs, on trouve que: (1-V2)Cos(Pi/huit)+Sin(Pi/huit)=0 CQFD.
Dernière édition par M.Marjani le Sam 22 Mai 2010, 16:45, édité 1 fois | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Sam 22 Mai 2010, 09:25 Sam 22 Mai 2010, 09:25 | |
| salam
exo 1 : facile
exo 2 : peut être une erreur : x1x4(x1x2x3x4) au lieu de x1x2( .....)
dans ce cas : (P1+P2).a = (P1P2)²
(2a-1).a = a².(a-1)² =====> équation 3e degré ???????
exo 3 :
1) -x^4 + x² = -[ (x²-1/2)² - 1/4 ] = 1/4 - (x²-1/2)² =< 1/4
donc le max = 1/4 atteint pour x²=1/2.
2) sous entendu : utiliser 1) poser OK = x , rayon = 1
l'aire = 1/2.OK.MN = 1/2.x.rac(1-x²).2 = x.rac(1-x²)
(l'aire)² = f(x) son max pour x²=1/2 =====> x= rac(2)/2.
------------------------
exo 4 : calcul......
. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Sam 22 Mai 2010, 13:45 Sam 22 Mai 2010, 13:45 | |
| Mr houssa, j'ai passé de l'deé mais quand r=1000 on serait perdu  Une autre chose que je n'ai pas compris, l'aire = 1/2.OK.MN = 1/2.x. rac(1-x²).2OK=(1/2)MN géneralement. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Sam 22 Mai 2010, 13:48 Sam 22 Mai 2010, 13:48 | |
| Exo 3 : J'imagine que c'est plutôt 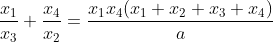 | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Sam 22 Mai 2010, 19:28 Sam 22 Mai 2010, 19:28 | |
| salam à marjani
d'après ta figure KM² = OM² - OK² (pythagore)= 1-x²
MN = 2.OK = 2.rac(1-x²)
------------------- | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Sam 22 Mai 2010, 19:44 Sam 22 Mai 2010, 19:44 | |
| - Sylphaen a écrit:
- Exo 3 :
J'imagine que c'est plutôt
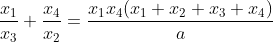 C'est ça, c'est édité. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Sam 22 Mai 2010, 19:46 Sam 22 Mai 2010, 19:46 | |
| - houssa a écrit:
- exo 3 :
1) -x^4 + x² = -[ (x²-1/2)² - 1/4 ] = 1/4 - (x²-1/2)² =< 1/4
donc le max = 1/4 atteint pour x²=1/2.
2) sous entendu : utiliser 1) poser OK = x , rayon = 1
l'aire = 1/2.OK.MN = 1/2.x.rac(1-x²).2 = x.rac(1-x²)
(l'aire)² = f(x) son max pour x²=1/2 =====> x= rac(2)/2.
------------------------
Même résultat. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Sam 22 Mai 2010, 20:00 Sam 22 Mai 2010, 20:00 | |
| - M.Marjani a écrit:
EX3:
Petite figure:

1/ f(x)=x²-x^4 <=> f(x)-x²=-x^4
x^4>=0 <=> -x^4=<0 => f(x)-x²=<0 <=> f(x)=<x²
Donc x² est une valeur maximal pour f(x).
2/ Soit f(x) la surface du triangle OMN.
S amn=(1/2)*OM*ON*Cos{MON}=(1/2)*OM²*Sin(MON)
(OM=r=cte)=> f(x)=(1/2)*r²*Sin(MON)=(1/2)*r²*x
Donc il faut que x soit maximal pour que la surface soit maximal.
Donc: x=Sin{MON}=1=Sin(Pi/2) [car: -1=<sinx=<1
ça veut dire qu'il faut que le triangle OMN soit rectangle en O pour que ça surface soit maximale.
=> On a: OK (واسط) [MN] et passant par O. Et: OMN=ONM
Donc: OMC est un trangle rectangle et issoecle en O.
=> OK=(1/2)MN (علاقة مترية).
EX4:
J'avais l'idée de partir dans une démonstration déjà faite sur Pi/8.. la méme idée de Mr Sylphaen, donc je vais changer de methode:
On a:+Sin(\frac{\Pi}{8})=\sqrt{2}*Cos(\frac{\Pi}{8}))
Multipliant chaque fois soit par Sin(Pi/ soit pas Cos(Pi/ soit pas Cos(Pi/ : :
+Cos(\frac{\Pi}{8})*Cos(\frac{\Pi}{8})=\sqrt{2}Cos^2(\frac{\Pi}{8}))
*Sin()+Sin^2(\frac{\Pi}{8} )=\sqrt{2}Cos(\frac{\Pi}{8} )*Sin(\frac{\Pi}{8} ))
*Sin(\frac{\Pi}{8})=(\sqrt{2}+1)(Sin^2(\frac{\Pi}{8})) & \\ Cos(\frac{\Pi}{8})*Sin(\frac{\Pi}{8})=(\sqrt{2-1)}(Cos(\frac{\Pi}{8})) & \end{Bmatrix})
=\frac{2-\sqrt{2}}{4}\Leftrightarrow Sin(\frac{\Pi}{8})=\frac{\sqrt{2-\sqrt{2}}}{2})
Cos(Pi/ et Sin(Pi/ et Sin(Pi/ £ [0,Pi/2] £ [0,Pi/2]
+Cos^2(\frac{\Pi}{8})=1\Leftrightarrow Cos(\frac{\Pi}{8})=\frac{\sqrt{2+\sqrt{2}}}{2})
Dans l'equation on remplace Cos(Pi/huit) et Sin(Pi/Huit) par leurs valeurs, on trouve que: (1-V2)Cos(Pi/huit)+Sin(Pi/huit)=0
CQFD. Pour l'exercice 3, la valeur maximale est une valeur précisée, non un inconnu. Pour l'exercice 4, je pense qu'il est interdit de faire une telle démarche. Pour moi, j'ai suivi ce procéssus: 1-Dessiner un cercle trigonométrique, de centre O, et de base (O,OI,OJ). 2-La droite OI coupe le cercle en B. 3-Choisir un point A tel que l'angle AOJ mesure Pi/4. 4-Soit H le projeté orthogonal de A sur OI. 5-Démontrer que l'angle ABI vaut Pi/8. 6-Calculer toutes les longueurs. 7-Déduire les valeurs exactes trigonométriques de Pi/8. 8-Déduire ce qui est demandé. Au plaisir. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Sam 22 Mai 2010, 21:07 Sam 22 Mai 2010, 21:07 | |
|
Dernière édition par M.Marjani le Sam 22 Mai 2010, 21:24, édité 3 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Sam 22 Mai 2010, 21:07 Sam 22 Mai 2010, 21:07 | |
| 3/ Sinon je complete ma démon, sans utiliser MN . Dans une cercle trigonomitrique On a montré que MON=Pi/2 => OMN=ONM=Pi/4 <=> Cos(Pi/4)= OK=V2/2
4/ oO, jamais entendu de ce que t'as dis! Pourquoi interdit donc? s'il est interdite, il vont dire cette phrase " sans trouver la valeur de Cos(x) et Sin(x)", ca reste juste donc.
+ Dis moi comment ABI=Pi/8?! [C'est faux] | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Mar 25 Mai 2010, 09:45 Mar 25 Mai 2010, 09:45 | |
| - M.Marjani a écrit:
- 3/ Sinon je complete ma démon, sans utiliser MN . Dans une cercle trigonomitrique On a montré que MON=Pi/2 => OMN=ONM=Pi/4 <=> Cos(Pi/4)= OK=V2/2
4/ oO, jamais entendu de ce que t'as dis! Pourquoi interdit donc? s'il est interdite, il vont dire cette phrase " sans trouver la valeur de Cos(x) et Sin(x)", ca reste juste donc.
+ Dis moi comment ABI=Pi/8?! [C'est faux] Pour ce qui est en rouge, tu as commencé par ce qui est demandé. Ce fait me semble illogique. Ensuite tu as commis une erreur dans ta démonstration quand tu as multiplié par sin(Pi/8 ). Pour ce qui est en vert, je pense que c'est une erreur d'inattention. Je vais poster une solution complète.
Dernière édition par nmo le Mar 25 Mai 2010, 14:46, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Mar 25 Mai 2010, 10:08 Mar 25 Mai 2010, 10:08 | |
| Pour le deuxième: On a l'équation ) admet deux racines 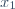 et 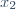 . Donc 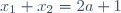 et 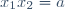 . Et on a l'équation ) admet deux racines 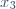 et 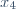 . Donc 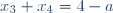 et  . Au travail: On a }{a}) . Donc }{a}) . Donc 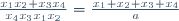 . Donc a}=\frac{2a+1+4-a}{a}) . Donc a}=\frac{a+5}{a}) . Donc  . Donc (a-1)) . Donc  . Donc 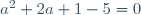 . Donc ^2-(\sqrt{5})^2=0) . Donc (a+1+\sqrt{5})=0) . Donc  ou  . Donc  ou 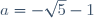 . Sauf erreur. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Mar 25 Mai 2010, 10:37 Mar 25 Mai 2010, 10:37 | |
| Pour le quatrième: Soit (C) un cercle trigonométrique de base (O,OI,OJ). La droite (OI) coupe ce cercle en un point B. A est un point tel que l'angle IOA mesure Pi/4. H est le projeté orthogonal de A sur (OI). Maintenant au travail: On a H le projeté orthogonal de A sur (OI). Donc AHO=Pi/2. (angle) On sait que AOH+HOA+HAO=Pi. (angles) Donc Pi/4+HOA+Pi/2=Pi. (angle) Donc HOA=Pi-Pi/2-Pi/4. (angle) Donc HOA=Pi/4. (angle) Ainsi le triangle AOH est isocèle et rectangle en H. Donc selon le théorème de pytagore, AH²+HO²=AO². Donc AH²+AH²=1². Donc 2AH²=1. Donc AH²=1/2. Donc AH=V(1/2). Donc AH=V2/2. Et OH=V2/2. On a BH=BO+OH. Donc BH=1+V2/2. Donc BH=(2+V2)/2. On a le triangle AHB est rectangle en H. Donc selon le théorème de pytagore, AH²+BH²=AB². Donc 1/2+[(2+V2)/2]²=AB². Donc 2/4+(4+4V2+2)/4=AB². Donc (8+4V2)/4=AB². Donc 2+V2=AB². Donc AB=V(2+V2). On a ABH=(1/2)AOH. Car ce sont deux angles se rapportant au même arc [AI]. Donc ABH=(1/2)*Pi/4. Donc ABH=Pi/8. Dans le triangle ABH: On a cos(Pi/8 )=cos(ABH). Donc cos(Pi/8 )=BH/AB. Donc cos(Pi/8 )=(2+V2)/2*1/V(2+V2). Donc cos(Pi/8 )=V(2+V2)/2. On a aussi sin(Pi/8 )=sin(ABH). Donc sin(Pi/8 )=AH/AB. Donc sin(Pi/8 )=V2/2*1/V(2+V2). Remplaçons maintenant: On a \cos{\frac{\pi}{8}}+\sin{\frac{\pi}{8}}=(1-\sqrt{2})(\frac{\sqrt{2+\sqrt{2}}}{2})+\frac{\sqrt{2}}{2}*\frac{1}{\sqrt{2+\sqrt{2}}}) . Donc \cos{\frac{\pi}{8}}+\sin{\frac{\pi}{8}}=(1-\sqrt{2})(\frac{\sqrt{2+\sqrt{2}}\sqrt{2+\sqrt{2}}}{2\sqrt{2+\sqrt{2}}})+\frac{\sqrt{2}}{2\sqrt{2+\sqrt{2}}}) . Donc \cos{\frac{\pi}{8}}+\sin{\frac{\pi}{8}}=\frac{(1-\sqrt{2})(2+\sqrt{2})}{2\sqrt{2+\sqrt{2}}}+\frac{\sqrt{2}}{2\sqrt{2+\sqrt{2}}}) . Donc \cos{\frac{\pi}{8}}+\sin{\frac{\pi}{8}}=\frac{2+\sqrt{2}-2\sqrt{2}-2+\sqrt{2}}{2\sqrt{2+\sqrt{2}}}) . Donc \cos{\frac{\pi}{8}}+\sin{\frac{\pi}{8}}=\frac{0}{2\sqrt{2+\sqrt{2}}}) . Donc \cos{\frac{\pi}{8}}+\sin{\frac{\pi}{8}}=0) . CQFD. Sauf faute de frappe.
Dernière édition par nmo le Mar 25 Mai 2010, 14:47, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Mar 25 Mai 2010, 11:07 Mar 25 Mai 2010, 11:07 | |
| Je vous présent une solution plus rigoureuse, à laquelle je n'ai pas fait attention lors du test: On a trouvé que  . Au travail: On a  . Donc ^2+\sin^2{\frac{\pi}{8}}=1) . Donc  . Donc 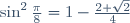 . Donc  . Donc  . D'autre part:  . Donc 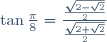 . Donc 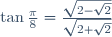 . Donc (\sqrt{2-\sqrt{2}})}{(\sqrt{2+\sqrt{2}})(\sqrt{2-\sqrt{2}})}) . Donc ^2}}) . Donc 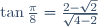 . Donc }{\sqrt{2}}) . Donc  . On a  . Donc \cos{\frac{\pi}{8}}=\sin{\frac{\pi}{8}}) . Donc \cos{\frac{\pi}{8}}=\sin{\frac{\pi}{8}}) . Donc \cos{\frac{\pi}{8}}+\sin{\frac{\pi}{8}}=0) . CQFD. J'attends vos remarques sur les deux methodes. Je me demande quelle est la solution la plus belle et qui montre que le condidat est si intelligent? | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Mar 25 Mai 2010, 12:46 Mar 25 Mai 2010, 12:46 | |
| - nmo a écrit:
- M.Marjani a écrit:
- 3/ Sinon je complete ma démon, sans utiliser MN . Dans une cercle trigonomitrique On a montré que MON=Pi/2 => OMN=ONM=Pi/4 <=> Cos(Pi/4)= OK=V2/2
4/ oO, jamais entendu de ce que t'as dis! Pourquoi interdit donc? s'il est interdite, il vont dire cette phrase " sans trouver la valeur de Cos(x) et Sin(x)", ca reste juste donc.
+ Dis moi comment ABI=Pi/8?! [C'est faux] Pour ce qui est en rouge, tu as commencé par ce qui est demandé.
Ce fait me semble illogique.
Ensuite tu as commis une erreur dans ta démonstration quand tu as multiplié par sin(Pi/ . .
Pour ce qui est en vert, je pense que c'est une erreur d'inattention.
Je vais poster une solution complète. Ce qui est en rouge: Vous pouvez posez cette question à votre prof.. si tu n'as pas convaincu  [On peut choisir des cotés ce qu'on veut, mais il faut arriver à l'autre coté.] 2/ Est-ce que c'est interdit de multiplier par Sin(Pi/  ou Cos(Pi/  ? Sinon précisez ou est l'error. [Normalement s'il y avait une error, je peux pas arriver aux résultats de Sin et Cos P/8..] Amicalement  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Mar 25 Mai 2010, 12:50 Mar 25 Mai 2010, 12:50 | |
| [quote="nmo"]Je vous présent une solution plus rigoureuse, à laquelle je n'ai pas fait attention lors du test: On a trouvé que  . J'attends vos remarques sur les deux methodes. Je me demande quelle est la solution la plus belle et qui montre que le condidat est si intelligent?[/quote] T'as utiliser ce que j'ai montré donc, t'as rendu votre methode plus longue.. C'est toi xD  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Mar 25 Mai 2010, 14:49 Mar 25 Mai 2010, 14:49 | |
| - M.Marjani a écrit:
- nmo a écrit:
- Je vous présent une solution plus rigoureuse, à laquelle je n'ai pas fait attention lors du test:
On a trouvé que  . .
J'attends vos remarques sur les deux methodes.
Je me demande quelle est la solution la plus belle et qui montre que le condidat est si intelligent?[/quote]
T'as utiliser ce que j'ai montré donc, t'as rendu votre methode plus longue..
C'est toi xD  En réalité, le problème est de déduire que tan(Pi/8 )=V2-1. C'est moi qui l'a trouvé dans l'autre démonstration. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Mar 25 Mai 2010, 15:37 Mar 25 Mai 2010, 15:37 | |
| - M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- 3/ Sinon je complete ma démon, sans utiliser MN . Dans une cercle trigonomitrique On a montré que MON=Pi/2 => OMN=ONM=Pi/4 <=> Cos(Pi/4)= OK=V2/2
4/ oO, jamais entendu de ce que t'as dis! Pourquoi interdit donc? s'il est interdite, il vont dire cette phrase " sans trouver la valeur de Cos(x) et Sin(x)", ca reste juste donc.
+ Dis moi comment ABI=Pi/8?! [C'est faux] Pour ce qui est en rouge, tu as commencé par ce qui est demandé.
Ce fait me semble illogique.
Ensuite tu as commis une erreur dans ta démonstration quand tu as multiplié par sin(Pi/ . .
Pour ce qui est en vert, je pense que c'est une erreur d'inattention.
Je vais poster une solution complète. Ce qui est en rouge: Vous pouvez posez cette question à votre prof.. si tu n'as pas convaincu  [On peut choisir des cotés ce qu'on veut, mais il faut arriver à l'autre coté.] [On peut choisir des cotés ce qu'on veut, mais il faut arriver à l'autre coté.]
2/ Est-ce que c'est interdit de multiplier par Sin(Pi/ ou Cos(Pi/ ou Cos(Pi/ ? Sinon précisez ou est l'error. [Normalement s'il y avait une error, je peux pas arriver aux résultats de Sin et Cos P/8..] ? Sinon précisez ou est l'error. [Normalement s'il y avait une error, je peux pas arriver aux résultats de Sin et Cos P/8..]
Amicalement  Si c'était calculez le côté gauche? Qu'est ce que tu vas faire? Une réponse: tu vas procéder de ma manière. Au plaisir. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Mar 25 Mai 2010, 17:52 Mar 25 Mai 2010, 17:52 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Jeu 27 Mai 2010, 11:56 Jeu 27 Mai 2010, 11:56 | |
| Le réciproquement dans ce cas c'est remplacer Cos et Sin avec leurs valeurs dans l'equation..
Essaie de ne pas écrire le tout Mr nmo (C'est la conseille des profs)
Le réciproquement que je vous propose est ainsi:
Tan(Pi/8 = V(V2-1)/V(V2+1)
=> Tan(pi/8 = V2-1 (1)
On a: Tan(Pi/8 = Sin(Pi/8 / Cos(Pi/8
Et D'aprés (1): Cos(pi/8 *(V2-1)-Sin(Pi/8 =0
Multipliant par (-): Cos(pi/8 *(1-V2)+Sin(Pi/8 =0
Ce qui est juste. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Jeu 27 Mai 2010, 12:11 Jeu 27 Mai 2010, 12:11 | |
| Pour le 3 EX:
Je ne suis pas convaincu Mr nmo ..
J'ai trouvé:
1/ f(x)=<x²
2/ OK=(1/2)MN (علاقة مترية).
1/ x est une valeur minimal pour la fonction.. Ok tu vas me dire pourquoi?: Je vais dire quand tu remplace x par 1 par exemple, tu auras f(1)=<1 ... Ce qui juste !
2/ OK=(1/2)MN : çela veut dire que NMO (xd) faut étre un triangle rectangle en O. Pourquoi ma démonstration est mieux de préciser un nombre? : Si tu prend MN=1 tu auras OK=1/2
Cela veut dire que: Ok=V2/2 n'est pas la valeur minimal de Ok de toute façon..
J'attend vos interventions.. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  Ven 28 Mai 2010, 10:51 Ven 28 Mai 2010, 10:51 | |
| - M.Marjani a écrit:
- Pour le 3 EX:
Je ne suis pas convaincu Mr nmo ..
J'ai trouvé:
1/ f(x)=<x²
2/ OK=(1/2)MN (علاقة مترية).
1/ x est une valeur minimal pour la fonction.. Ok tu vas me dire pourquoi?: Je vais dire quand tu remplace x par 1 par exemple, tu auras f(1)=<1 ... Ce qui juste !
2/ OK=(1/2)MN : çela veut dire que NMO (xd) faut étre un triangle rectangle en O. Pourquoi ma démonstration est mieux de préciser un nombre? : Si tu prend MN=1 tu auras OK=1/2
Cela veut dire que: Ok=V2/2 n'est pas la valeur minimal de Ok de toute façon..
J'attend vos interventions.. On dit que f est majorée sur I lorsqu'il existe un réel M tel que, pour tout x de I, f(x)=<M. Et il faut que l'équation f(x)=M admette des solutions. Chose qui n'est pas présente dans ta démonstration. La réponse de houssa est juste et ce qui est en rouge l'est aussi. Au plaisir. P.S: j'aime que mes réponses soient parfaites afin de ne pas laisser quelqu'un me critiquer. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: L'olympiade de settat: (troisième étape) Sujet: Re: L'olympiade de settat: (troisième étape)  | |
| |
|
  | |
| | L'olympiade de settat: (troisième étape) |  |
|
