Le carré complet ( Arithmetique )

Bonjour,..

Et MERCI !!

voila un contre exemple
pr la derniere proprieté a=4 et b=4 leur somme n'est po un carré parfait et y'en a plusieurs contre exemples

nononabil::
Merci pour votre reponse, mais a^2+b^2 est juste un exemple
l'important, c'est le modulo 4 ou 3 ...
L'exemple exacte est "2(ab+bc+ca)=3[8]" -> n'est pas complet
si on a "..=4 ou 1 ou 0 [8]" -> carré complet.
Je veux la regle, pourqoi 4 et 1 et 0 et ne pas 7 par exemple

salut
Comme remarque: on dit pas carré complet mais carré Parfait !

ce qui concerne votre question il y a pas des methodes precises pr ton exemple deja car:

a²+b² = (a+b)²-2ab = (a-b)² + 2ab ....

Je veux juste la methode en utilisant l'arithmetique
Je sais que a^2+b^2 est faux

Pourquoi trimballer partout des 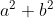inefficaces ? Posons et extirpons-nous de fait de cette misère.
De plus, l'on a, et ce qui est très classique :

Par contraposée, tu peux déjà savoir quand un entier n'est pas un carré parfait.

mego c une probleme de baccalaureat je pense 2006 suis les etapes en le resolvant et tu vas savoir bonne chance
demain je vais poster ma reponse pr donner une chance aux autres de le decouvrir

bonjour
si n est imppair
n=2k+1 ==> n²=4k²+4k+1=4k(k+1)+1
on sé bien que k(k+1)=2q
donc n²=8q+1 donc n²=1modulo(
si n est pair
n=2k ==> n=4q+2 ou n=4q
donc n²=16q²+16q+4=8(2q²+2q)+4==> n=4modulo (
ou n²=8(2q²) ==> n²=0modulo(
A+