Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Own And Easy . Sujet: Own And Easy .  Ven 26 Mar 2010, 14:04 Ven 26 Mar 2010, 14:04 | |
| Soit a,b,c>0 avec a+b+c=1 Montrer que : 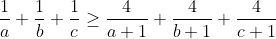 Et : 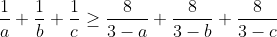 | |
|
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Own And Easy . Sujet: Re: Own And Easy .  Ven 26 Mar 2010, 19:26 Ven 26 Mar 2010, 19:26 | |
| | |
|
.
Maître
 Nombre de messages : 296 Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
 |  Sujet: Re: Own And Easy . Sujet: Re: Own And Easy .  Dim 28 Mar 2010, 21:18 Dim 28 Mar 2010, 21:18 | |
| Pour la deuxième on a par Titu :  , une application imédiate par Jensen donne :  Puisque la fonction  est concave sur  ... Je vais reflechir pour prouver la 1 ère d'une autre façon | |
|
Contenu sponsorisé
 |  Sujet: Re: Own And Easy . Sujet: Re: Own And Easy .  | |
| |
|
