| | exercice d'olympide khouribga 2010 |  |
|
|
| Auteur | Message |
|---|
chaimaa1994
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 30
Localisation : maroc pays des merveilles
Date d'inscription : 17/03/2010
 |  Sujet: exercice d'olympide khouribga 2010 Sujet: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 12:23 Dim 18 Avr 2010, 12:23 | |
| ليكن n عدداصحيحا طبيعيا غير منعدم
بين أن العدد ليكن عدداصحيحا طبيعيا غير منعدم
بين أن العدد
7^(6n+3)+3^(8n+4)
يقبل القسمة على106 | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 13:01 Dim 18 Avr 2010, 13:01 | |
| - chaimaa1994 a écrit:
ليكن n عدداصحيحا طبيعيا غير منعدم
بين أن العدد ليكن عدداصحيحا طبيعيا غير منعدم
بين أن العدد
7^(6n+3)+3^(8n+4)
يقبل القسمة على106 Posons la suite u telle que : 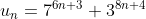 Nous avons : 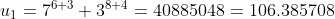 Supposons que 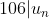 et montrons que 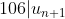 Nous avons : +3}+3^{8(n+1)+4}\\\Leftrightarrow%20u_{n+1}=7^{6n+6+3}+3^{8n+8+4}\\\Leftrightarrow%20u_{n+1}=7^67^{6n+3}+3^83^{8n+4}\\\Leftrightarrow%20u_{n+1}=117649.7^{6n+3}+6561.3^{8n+4}\\\Leftrightarrow%20u_{n+1}=6561.7^{6n+3}+111088.7^{6n+3}+6561.3^{8n+4}\\\Leftrightarrow%20u_{n+1}=6561(7^{6n+3}+3^{8n+4})+111088.7^{6n+3}%20\\\Leftrightarrow%20u_{n+1}=6561u_{n}+106.1048.7^{6n+3}) Et donc si 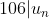 , 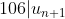 Concluons que : 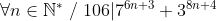 CQFD Sauf erreur. Au plaisir !  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 19:27 Dim 18 Avr 2010, 19:27 | |
| Vous avez passez les Olymp du troisiéme phase ?
Dernière édition par M.Marjani le Dim 18 Avr 2010, 19:39, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 19:30 Dim 18 Avr 2010, 19:30 | |
| Joli Mr Mizmaz, toujours à la hauteur! s'agit-il d'une methode de 1BAC non? Mon essaie: ----------------------------------------------------------------------------------- } + 3^{4(2n+1)}) Prenons : X=2n+1 => 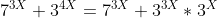 Donc : ^{3X} + 3^{3X}*3^X=343^X + 27^X*3^X) => 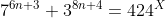 On a: ^X=(4*106)^{2n+1}=4^{2n}*4*106^{2n}*106|106) Ce qui términe la démonstration. CQFD | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:08 Dim 18 Avr 2010, 20:08 | |
| | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:11 Dim 18 Avr 2010, 20:11 | |
| une autre métohde bien plus facile
en remarkant que
7^3=3.106+25 ==> (7^3)^(2K+1) =25^(2K+1)[106]
et 3^4=106-25 ==> (3^4)^(2K+1)=-25^(2K+1)[106]
donc 106 divise (7^(6k+3)+3^(8k+4)
A+ | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:13 Dim 18 Avr 2010, 20:13 | |
| - darkpseudo a écrit:
la partie ou tu passe de 7^6+3n +3^8n+4 est fausse a mon avis , car on ne factorise pas avec des puissances ! Quand t'as appris ça? C'est normal .. ce sont des chiffres non? | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:18 Dim 18 Avr 2010, 20:18 | |
| donc dapres toi a²+b²=(a+b)² ...???!!! | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:19 Dim 18 Avr 2010, 20:19 | |
| | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:19 Dim 18 Avr 2010, 20:19 | |
| Voila ma réponse , j'ai utilisé quelques outils de base de l'arithmétique que vous étudirez l'année prochaine inchalah :
7^(6n+2) = 7^6n*7^3
le reste de la division euclydéenne de 7^3 par 106 est 25
celui de 7^6n est 95^n ( en faite on a 7^6n-95^n est divisible par 106 )
donc il nous suffit de prendre 95^n*25
de même pour 3^(8n+3)=3^8n*81
ce qui revient a étudier 95^n*81 ( il suffit d'utiliser la calculatrice en ignorant les puissance vous trouverez que 3^8-95 est divisible par 106 et pui il y a une regle qui ne permet d'elever a la puissance n )
donc le reste de la division euclydienne de 7^(6n+2)+3^(8n+3) est le même que celui de 95^n*81+95^n*25 on factorisant par 95^n on trouve 95^n*106 donc 106 divise ce nombre CQFD
Sauf erreur | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:22 Dim 18 Avr 2010, 20:22 | |
| - darkpseudo a écrit:
- Voila ma réponse , j'ai utilisé quelques outils de base de l'arithmétique que vous étudirez l'année prochaine inchalah :
7^(6n+2) = 7^6n*7^3
le reste de la division euclydéenne de 7^3 par 106 est 25
celui de 7^6n est 95^n ( en faite on a 7^6n-95^n est divisible par 106 )
donc il nous suffit de prendre 95^n*25
de même pour 3^(8n+3)=3^8n*81
ce qui revient a étudier 95^n*81 ( il suffit d'utiliser la calculatrice en ignorant les puissance vous trouverez que 3^8-95 est divisible par 106 et pui il y a une regle qui ne permet d'elever a la puissance n )
donc le reste de la division euclydienne de 7^(6n+2)+3^(8n+3) est le même que celui de 95^n*81+95^n*25 on factorisant par 95^n on trouve 95^n*106 donc 106 divise ce nombre CQFD
Sauf erreur Peux-tu m'expliquer s'il te plait pourquoi tu as dit ça : «la partie ou tu passe de 7^6+3n +3^8n+4 est fausse a mon avis , car on ne factorise pas avec des puissances !» ?  | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:22 Dim 18 Avr 2010, 20:22 | |
| | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:24 Dim 18 Avr 2010, 20:24 | |
| j'ai pas compris ce ke t entrain de faire mais ma solution est bien plus rapide ... | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:27 Dim 18 Avr 2010, 20:27 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:30 Dim 18 Avr 2010, 20:30 | |
| | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:30 Dim 18 Avr 2010, 20:30 | |
| - houssam110 a écrit:
- j'ai pas compris ce ke t entrain de faire mais ma solution est bien plus rapide ...
Elle est plus rapide pour une raison , tu a utiliser la congruence sans l'expliquer alors que moi j'ai essayer de simplifier car on est dans la section tronc commun et qu'il sont supposé ne pas l'avoir encor étudier tu vois ?? | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 20:32 Dim 18 Avr 2010, 20:32 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  Dim 18 Avr 2010, 21:28 Dim 18 Avr 2010, 21:28 | |
| [quote="darkpseudo exemple ce qu'il a dit c'est comme si 5^2+3^2=8^2 ce qui est faux ^^ on fait on a la relation x^n+y^n= 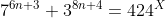 voila de quoi j'ai parler cette partie est fausse[/quote] Ahaa.. Ok, c'est vrai, c'est un faute d'innatention, je pense que j'ai vu 3X au lieu de 3^X. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: exercice d'olympide khouribga 2010 Sujet: Re: exercice d'olympide khouribga 2010  | |
| |
|
  | |
| | exercice d'olympide khouribga 2010 |  |
|
