| | Bel exercice dolymp |  |
|
|
| Auteur | Message |
|---|
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Bel exercice dolymp Sujet: Bel exercice dolymp  Dim 25 Avr 2010, 17:35 Dim 25 Avr 2010, 17:35 | |
| définissez l3adad Sahih tabi3i M pour: M-61 et M+40 mouraba3ayn de deux nombres s ahihayne tabi3iyayn  | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 17:48 Dim 25 Avr 2010, 17:48 | |
| - A446 a écrit:
- définissez l3adad Sahih tabi3i M pour:
M-61 et M+40 mouraba3ayn de deux nombres s
ahihayne tabi3iyayn  Nous avons le système suivant : ^2%20\end{matrix}\right.%20\\%20\Leftrightarrow%20\left\{\begin{matrix}%20M=s^2+61\\M=s^2+2s-39%20\end{matrix}\right.\\\Rightarrow%20s^2+61=s^2+2s-39\\\Leftrightarrow%202s-100=0\\\Leftrightarrow%20s=50) Donc : 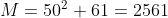 Sauf erreur. Au plaisir !  | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 18:02 Dim 25 Avr 2010, 18:02 | |
| pq t'es parti de M+40=(s+1)^2
et M-61=s^2
alors que les deux nombres x^2=M-61 et y^2=M+40
il n y pas de relation entre x et y | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 18:10 Dim 25 Avr 2010, 18:10 | |
| - A446 a écrit:
- pq t'es parti de M+40=(s+1)^2
et M-61=s^2
alors que les deux nombres x^2=M-61 et y^2=M+40
il n y pas de relation entre x et y J'ai cru comprendre qu'ils étaient successifs. (Moutatabi3ayne) Au plaisir !  | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 18:13 Dim 25 Avr 2010, 18:13 | |
| ah non pas du tout sa serai trop facil
Tu devrai reessayer Bonne chance | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 18:18 Dim 25 Avr 2010, 18:18 | |
| On a m-61=a^2.
Et m+40=b^2.
Donc b^2-a^2=m+40-m+61.
Donc (a-b)(a+b)=101.
Les diviseurs de 101 sont 1 et 101 car il est premier.
Donc a-b=1 et a+b=101.
Donc a+b+a-b=1+101.
Donc 2a=102.
Donc a=51.
On a m-61=51^2.
Donc m-61=2601.
Donc m=2662.
J'espère que c'est juste. | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 18:38 Dim 25 Avr 2010, 18:38 | |
| Ce qui est faux
ta fait une faute dans l'identité remarquable
b^2-a^2=(b-a)(b+a)
et non: (a-b)(a+b) | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 18:42 Dim 25 Avr 2010, 18:42 | |
| Sinon
tu devrai changer de méthode
car avec celle-ci tu tourne en rond | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 19:06 Dim 25 Avr 2010, 19:06 | |
| slt , la soluc est M=2561 | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 19:09 Dim 25 Avr 2010, 19:09 | |
| sans la méthode,
la solution ne vaut rien
(n'oublie pas que c'est un exo d'olympiade) | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 19:25 Dim 25 Avr 2010, 19:25 | |
| On trouve cette solution en utilisant la méthode de nmo, je pense. Les deux nombres sont naturellement successifs.  | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Dim 25 Avr 2010, 20:20 Dim 25 Avr 2010, 20:20 | |
| ok ^^ : voila : supposons que
M-61=S² et M+40=K² (K,S)£N²
M+40-101=M-61=K²-101=S²
101= (K-S)(K+S)
donc on aurait deux cas : (un nombre premier a 2 diviseurs dans N)
soit K-S=1 et K+S=101
ou K-S=101 et K+S=1 ==> absurde (K+S> K-S)
donc
2K=102 ==> k=51 et S=50
alors M=S²+61 =2500+61=2561 , et meme en remplacons K avec sa valeur on aurait meme resultat !!
Dernière édition par master le Ven 28 Mai 2010, 23:12, édité 1 fois | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  Lun 26 Avr 2010, 17:56 Lun 26 Avr 2010, 17:56 | |
| C'est bon  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Bel exercice dolymp Sujet: Re: Bel exercice dolymp  | |
| |
|
  | |
| | Bel exercice dolymp |  |
|
