Exercice d'anciens olymp

Bonjour , je viens découvrir votre forum il y a 2 jours il est tout simplement fantastique , je suis en T.C.S comme tout les membres de la catégorie ou je poste , je suis de casa et je suis qualifié pour la 3ème phase qui aura lieu vendredi inchalah , par contre quand je vois les exercices que vous postez et les soluces des autres je ne pense pas que j'aurais de la chance pour me qualifier mais tbarklah 3likoum

Sinon revenons a nos moutons j'ai 2 exercices dont je voudrais avoir la solution et je pense qu'ils seront très faciles pour vous :
EXERCICE 1 :
Soit p et q deux nombre entiers positifs successifs , démontrez que le nombre suivant est un carré complet : p² + q² + (pq)²

EXERCICE 2 :
1) simplifiez : (a-b)(a²+ab+b²) ( super facile pour des olymp ca lol )
2) démontrez que 3^36 - 2^36 divise 19 .

Merci à votre aide et bonne chance !

salam
pour exo2
(a-b)(a²+ab+b²)= a^3 - b^3
et pour la deuxieme on a
3^36 - 2^36= (3^3)^12 - (2^3)^12 = 27^12 - 8^12 = (27 -8 )(27^11 + 27^10.8 ........+8^27) =19.k
d'ou la conclusion ..
P.S bienvenue Mim^^

Bienvenue Mr Mim.

1/On a: 0=<p=q+1
Donc:
p² + q² + (pq)²
=p²+(p+1)²+[p(p+1)]²
=2p²+2p+1+p²(p+1)²
=2p(p+1)+p²(p+1)²+1
=[p(p+1)+1]²

CQFD.

Pour Le Premier:
Posons:q=p+1 (Deux entiers Successifs)
A=p²+q²+(pq)²
=2p²+2p+1+p²(p²+2p+1)
=2(p²+p)+(p^4+2p^3+p²)+1
=(p²+p)²+2(p²+p)+1
=((p²+p)+1)²
D'ou le Résultat!
Bienvenu Cher Mim,Et T'inquiéte Nchaalah Tu Va Etre Qualifié!

Ouppps,On A Répondu au Meme Instant M.Marjanii!

Re , merci pour votre rapidité et votre temps de réaction qui démontre votre interet a l'égard des jeunes amateurs de maths et aussi pour m'avoir souhaité la bienvenue parmi vous , pour le 1er exo j'ai très bien compris la solution par contre l'exo 2 j'ai pas compris cette partie :

master a écrit:

= (27 -8 )(27^11 + 27^10.8 ........+8^27) =19.k

Merci de m'éclaircir si possible la représentations des ... ^^

27-8=19 alors =19(27^11..............)
=19k

c un peu long et meme si pas interessant de l'ecrire ... mais
c b1 claire que
et pour b1 eclaire dans notre cas on a n=12 et a=27 et b=8
donc si on remplace avec ces valeures on deduit ce que j'ai ecrit ^^
Au plaisir !!

Mr master, ta solution proposé faut qu'il utilise: (a-b)(a²+ab+b²)= a^3 - b^3 , c'est necessaire.

Je donne une autre methode pour le 2éme:
(a-b)(a²+ab+b²)=a^3 -b^3
On a: 3^36-2^36
=(3^12)^3 -(2^12)^3
=[(3^3)^4 -(2^3)^4][3^24 +6^12 +2^24]
=[3^6-2^6][3^6+2^6][3^24 +6^12 +2^24]
=[3^3-2^3][3^3+2^3][3^6+2^6][3^24 +6^12 +2^24]
=19[3^3+2^3][3^6+2^6][3^24 +6^12 +2^24]

D'ou le résultat ...

W.Elluizi a écrit:

Ouppps,On A Répondu au Meme Instant M.Marjanii!

Pas grave cher, voilà deux methodes pour la prouver donc.

master a écrit:

c un peu long et meme si pas interessant de l'ecrire ... mais
c b1 claire que
et pour b1 eclaire dans notre cas on a n=12 et a=27 et b=8
donc si on remplace avec ces valeures on deduit ce que j'ai ecrit ^^
Au plaisir !!

C'est bien, mais il faut utiliser la question d'avant. Sinon, pourquoi donnent-ils la premiére question à ton avis?

mmmmm ok , mais Mr .Marjani c pas annoncé je crois sinon ils vont dire demontrer apres la premiere question
mais en tt cas il ya de plusieure soluc ..^^

deux nouveaux exercices pour vous .

EXO 1 :
Soit a , b , c les triangles d'un coté avec : a + b + c = 1
démontre que : a² + b² + c² +4abc > 1/2

EXO 2 :
a et b sont deux nombre positifs avec a < b :
A = (1 + a + a² + ... + a^7 ) / ( 1 + a + a² + .... + a ^8 )
B= ( 1 + b + b² + ... + b^7 ) / ( 1 + b + b² + ... + b^8 )

Faites la différence entre A et B

Mim a écrit:

deux nouveaux exercices pour vous .

EXO 1 :
Soit a , b , c les triangles d'un coté avec : a + b + c = 1
démontre que : a² + b² + c² +4abc > 1/2

EXO 2 :
a et b sont deux nombre positifs avec a < b :
A = (1 + a + a² + ... + a^7 ) / ( 1 + a + a² + .... + a ^8 )
B= ( 1 + b + b² + ... + b^7 ) / ( 1 + b + b² + ... + b^8 )

Faites la différence entre A et B

Premiére EXO c'est faux.
Contre exemple: prenons: a=b=c=1/3 => a² + b² + c² +4abc=13/27<1/2
2/ Déja posté dans le sujet " EXERCICE D'OLYMPIADE " je pense. Ils ont trouvé A>B si je me souvien.

La volonté a écrit:

Posant a=x+y; b=y+z; c=x+z <=> x+y+z=1/2





Ce qui est juste..

La solution du premier exercice.

Pour le deuxième exercice:
Premièrement, on a et .
Donc et .
On a .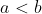
Donc .
Donc .
Et ...
Et .
La somme de ces inégalités donne .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Sauf erreur de frappe.

nmo a écrit:

La volonté a écrit:

Posant a=x+y; b=y+z; c=x+z <=> x+y+z=1/2





Ce qui est juste..

La solution du premier exercice.

La methode de "La volonté" semble juste.
Mais si nous prenons: a=0,b=0,c=1 <=> 1<1/2
Ce qui est faux .. :S

nmo a écrit:

La volonté a écrit:

Posant a=x+y; b=y+z; c=x+z <=> x+y+z=1/2





Ce qui est juste..

La solution du premier exercice.

La methode de "La volonté" semble juste.
Mais si nous prenons: a=0,b=0,c=1 <=> 1<1/2
Ce qui est faux .. :S

M.Marjani a écrit:

nmo a écrit:

La volonté a écrit:

Posant a=x+y; b=y+z; c=x+z <=> x+y+z=1/2





Ce qui est juste..

La solution du premier exercice.

La methode de "La volonté" semble juste.
Mais si nous prenons: a=0,b=0,c=1 <=> 1<1/2
Ce qui est faux .. :S

Si on prend a=0.
Alors x+y=0.
Donc x=0 et y=0.
Ce qui est faux.
Je pense qu'elle a oublié de le mensionner au début.
Cependant, il ne faut pas être si naif.

nmo a écrit:

M.Marjani a écrit:

nmo a écrit:

La volonté a écrit:

Posant a=x+y; b=y+z; c=x+z <=> x+y+z=1/2





Ce qui est juste..

La solution du premier exercice.

La methode de "La volonté" semble juste.
Mais si nous prenons: a=0,b=0,c=1 <=> 1<1/2
Ce qui est faux .. :S

Si on prend a=0.
Alors x+y=0.
Donc x=0 et y=0.
Ce qui est faux.
Je pense qu'elle a oublié de le mensionner au début.
Cependant, il ne faut pas être si naif.

Oui, mais le probléme qu'il ya d'autre réels £[0,1] non le 0 seulement. ce qui rendent l'inegalité toute fausse.

nmo a écrit:

La solution de l'exercice:
On a a, b, et c des longueurs des côtés d'un triagle.
Donc, d'après l'inégalité triangulaire, a<b+c.
Donc a+a<a+b+c.
Donc 2a<1.
Donc a<1/2.
De même b<1/2.
Et c<1/2.
Posons maintenant a=1/2-x, b=1/2-y, et c=1/2-z.
On a a<1/2 et b<1/2 et c<1/2.
Donc 0<1/2-a et 0<1/2-b et 0<1/2-c.
Donc 0<1/2-(1/2-x) et 0<1/2-(1/2-y) et 0<1/2-(1/2-z).
Donc 0<1/2-1/2+x et 0<1/2-1/2+y et 0<1/2-1/2+z.
Donc 0<x et 0<y et 0<z.
Et on a a+b+c=1.
Donc 1/2-x+1/2-y+1/2-z=1.
Donc 1/2=x+y+z.
D'autre part, on fait la soustraction a²+b²+c²+4abc-1/2=(1/2-x)²+(1/2-y)²+(1/2-z)²+4(1/2-x)(1/2-y)(1/2-z)-1/2.
Donc a²+b²+c²+4abc-1/2=1/4-2*1/2*x+x²+1/4-2*1/2*y+y²+1/4-2*1/2*z+z²+4(1/4-1/2*y-1/2*x+xy)(1/2-z)-1/2.
Donc a²+b²+c²+4abc-1/2=3/4-1/2-x+x²-y+y²-z+z²+4(1/8-1/4*z-1/4*y+1/2*yz-1/4*x+1/2*xz+1/2*xy-xyz).
Donc a²+b²+c²+4abc-1/2=1/4-(x+y+z)+x²+y²+z²+1/2-z-y+2yz-x+2xz+2xy-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4-1/2+(x²+y²+z²+2xy+2xz+2yz)+1/2-(x+y+z)-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4+(x+y+z)²-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4+(1/2)²-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4+1/4-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=1/2-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=-4xyz.
On a déja démontré que 0<x et 0<y et 0<z.
Donc 0<xyz.
Donc -4xyz<0.
Donc a²+b²+c²+4abc-1/2<0.
Donc a²+b²+c²+4abc<1/2.
CQFD.
Sauf faute de frappe.

Voici ma propre solution.
Au plaisir.