Exercice d'anciens olymp

Pour le deuxième exercice:
Premièrement, on a et .
Donc et .
On a .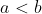
Donc .
Donc .
Et ...
Et .
La somme de ces inégalités donne .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Sauf erreur de frappe.

nmo a écrit:

La volonté a écrit:

Posant a=x+y; b=y+z; c=x+z <=> x+y+z=1/2





Ce qui est juste..

La solution du premier exercice.

La methode de "La volonté" semble juste.
Mais si nous prenons: a=0,b=0,c=1 <=> 1<1/2
Ce qui est faux .. :S

nmo a écrit:

La volonté a écrit:

Posant a=x+y; b=y+z; c=x+z <=> x+y+z=1/2





Ce qui est juste..

La solution du premier exercice.

La methode de "La volonté" semble juste.
Mais si nous prenons: a=0,b=0,c=1 <=> 1<1/2
Ce qui est faux .. :S

M.Marjani a écrit:

nmo a écrit:

La volonté a écrit:

Posant a=x+y; b=y+z; c=x+z <=> x+y+z=1/2





Ce qui est juste..

La solution du premier exercice.

La methode de "La volonté" semble juste.
Mais si nous prenons: a=0,b=0,c=1 <=> 1<1/2
Ce qui est faux .. :S

Si on prend a=0.
Alors x+y=0.
Donc x=0 et y=0.
Ce qui est faux.
Je pense qu'elle a oublié de le mensionner au début.
Cependant, il ne faut pas être si naif.

nmo a écrit:

M.Marjani a écrit:

nmo a écrit:

La volonté a écrit:

Posant a=x+y; b=y+z; c=x+z <=> x+y+z=1/2





Ce qui est juste..

La solution du premier exercice.

La methode de "La volonté" semble juste.
Mais si nous prenons: a=0,b=0,c=1 <=> 1<1/2
Ce qui est faux .. :S

Si on prend a=0.
Alors x+y=0.
Donc x=0 et y=0.
Ce qui est faux.
Je pense qu'elle a oublié de le mensionner au début.
Cependant, il ne faut pas être si naif.

Oui, mais le probléme qu'il ya d'autre réels £[0,1] non le 0 seulement. ce qui rendent l'inegalité toute fausse.

nmo a écrit:

La solution de l'exercice:
On a a, b, et c des longueurs des côtés d'un triagle.
Donc, d'après l'inégalité triangulaire, a<b+c.
Donc a+a<a+b+c.
Donc 2a<1.
Donc a<1/2.
De même b<1/2.
Et c<1/2.
Posons maintenant a=1/2-x, b=1/2-y, et c=1/2-z.
On a a<1/2 et b<1/2 et c<1/2.
Donc 0<1/2-a et 0<1/2-b et 0<1/2-c.
Donc 0<1/2-(1/2-x) et 0<1/2-(1/2-y) et 0<1/2-(1/2-z).
Donc 0<1/2-1/2+x et 0<1/2-1/2+y et 0<1/2-1/2+z.
Donc 0<x et 0<y et 0<z.
Et on a a+b+c=1.
Donc 1/2-x+1/2-y+1/2-z=1.
Donc 1/2=x+y+z.
D'autre part, on fait la soustraction a²+b²+c²+4abc-1/2=(1/2-x)²+(1/2-y)²+(1/2-z)²+4(1/2-x)(1/2-y)(1/2-z)-1/2.
Donc a²+b²+c²+4abc-1/2=1/4-2*1/2*x+x²+1/4-2*1/2*y+y²+1/4-2*1/2*z+z²+4(1/4-1/2*y-1/2*x+xy)(1/2-z)-1/2.
Donc a²+b²+c²+4abc-1/2=3/4-1/2-x+x²-y+y²-z+z²+4(1/8-1/4*z-1/4*y+1/2*yz-1/4*x+1/2*xz+1/2*xy-xyz).
Donc a²+b²+c²+4abc-1/2=1/4-(x+y+z)+x²+y²+z²+1/2-z-y+2yz-x+2xz+2xy-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4-1/2+(x²+y²+z²+2xy+2xz+2yz)+1/2-(x+y+z)-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4+(x+y+z)²-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4+(1/2)²-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4+1/4-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=1/2-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=-4xyz.
On a déja démontré que 0<x et 0<y et 0<z.
Donc 0<xyz.
Donc -4xyz<0.
Donc a²+b²+c²+4abc-1/2<0.
Donc a²+b²+c²+4abc<1/2.
CQFD.
Sauf faute de frappe.

Voici ma propre solution.
Au plaisir.