|
| | Olympiade de Kénitra (2nd tour) |  |
|
+4master M.Marjani W.Elluizi Dijkschneier 8 participants | |
| Auteur | Message |
|---|
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Dim 16 Mai 2010, 13:49 Dim 16 Mai 2010, 13:49 | |
| Bien joué Dijcka, méme chose, je l'ai fais avec Delta, et j'ai remarquer que Si a=b donc S=L'ensemble vide.. | |
|   | | Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Dim 16 Mai 2010, 14:27 Dim 16 Mai 2010, 14:27 | |
| Je viens de trouver une solution simple pour l'exo 5 !  Noter :   Soit x le nombre des éléments de A dans {1,2...,n} Alors on a :   Ainsi :  D'autre part on a :  Et finalement :  | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Dim 16 Mai 2010, 14:54 Dim 16 Mai 2010, 14:54 | |
| Soyez plus précis Sylphaen. - Citation :
- Soit x le nombre des éléments de A dans {1,2...,n}
Qu'est-ce ça veut dire ? - Citation :
 D'où ça vient, ça ? Qu'est-ce que ||1,n|| ? - Citation :
 Pourquoi ? | |
|   | | Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Dim 16 Mai 2010, 15:02 Dim 16 Mai 2010, 15:02 | |
| [|1,n|]=[1,n] ∩ Z ={1,2,..n}
On a x élément de A dans [|1,n|] alors :
a_1,a_2,...a_x appartient a [|1,n|]
par conséquent on a (n-x) élément de B dans [|1,n|]
donc b_n,b_{n-1}...b_{x+1} appartient à [|1,n|]
De la même façon on prouve que :
b_1,b_2,..b_x appartient à [|n+1,2n|]
et
a_n,a_{n-1},..a_{x+1} appartient à [|n+1,2n|]
Et puisque a_1,a_2,..a_x appartient à [|1,n|]
et b_1,b_2...b_x appartient à [|n+1,2n|]
alors pour tous i dans [|1,n|] on a |b_i-a_i|=b_i-a_i
de même on obtient notre somme .. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Dim 16 Mai 2010, 15:40 Dim 16 Mai 2010, 15:40 | |
| - Sylphaen a écrit:
- [|1,n|]=[1,n] ∩ Z ={1,2,..n}
On a x élément de A dans [|1,n|] alors :
a_1,a_2,...a_x appartient a [|1,n|]
par conséquent on a (n-x) élément de B dans [|1,n|]
donc b_n,b_{n-1}...b_{x+1} appartient à [|1,n|]
De la même façon on prouve que :
b_1,b_2,..b_x appartient à [|n+1,2n|]
et
a_n,a_{n-1},..a_{x+1} appartient à [|n+1,2n|]
Et puisque a_1,a_2,..a_x appartient à [|1,n|]
et b_1,b_2...b_x appartient à [|n+1,2n|]
alors pour tous i dans [|1,n|] on a |b_i-a_i|=b_i-a_i
de même on obtient notre somme .. Bravo ! Légère faute quoique, il ne s'agit pas d'un i allant de 1 à n, mais d'un i allant de 1 à x. | |
|   | | dhiab
Féru

 Nombre de messages : 56 Nombre de messages : 56
Age : 61
Date d'inscription : 27/01/2010
 | |   | | Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Dim 16 Mai 2010, 18:09 Dim 16 Mai 2010, 18:09 | |
| - Dijkschneier a écrit:
- Sylphaen a écrit:
- [|1,n|]=[1,n] ∩ Z ={1,2,..n}
On a x élément de A dans [|1,n|] alors :
a_1,a_2,...a_x appartient a [|1,n|]
par conséquent on a (n-x) élément de B dans [|1,n|]
donc b_n,b_{n-1}...b_{x+1} appartient à [|1,n|]
De la même façon on prouve que :
b_1,b_2,..b_x appartient à [|n+1,2n|]
et
a_n,a_{n-1},..a_{x+1} appartient à [|n+1,2n|]
Et puisque a_1,a_2,..a_x appartient à [|1,n|]
et b_1,b_2...b_x appartient à [|n+1,2n|]
alors pour tous i dans [|1,n|] on a |b_i-a_i|=b_i-a_i
de même on obtient notre somme .. Bravo ! Légère faute quoique, il ne s'agit pas d'un i allant de 1 à n, mais d'un i allant de 1 à x. Oué bien vu !  | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Lun 17 Mai 2010, 11:58 Lun 17 Mai 2010, 11:58 | |
| Bien joué Sylphaen, vraiment tu es génial  Dijckashiener félicitation pour le 5/6, et si tu peux voir les résultats de notre délégation, donne moi les infos. Merci. + J'ai lu dans une fiche, que ceux qui n'ont pas qualifié dans la dérniere phase, ne vont participer aux olympiades de 1BAC SM  Vous avez des idées sur ça? | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Lun 17 Mai 2010, 12:34 Lun 17 Mai 2010, 12:34 | |
| - Dijkschneier a écrit:
Vous n'aviez pas semblé prendre ma remarque avec un air d'intérêt, alors laissez-moi vous montrer explicitement votre faute.
Résolvons l'équation 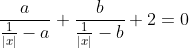
L'équation est définie ssi 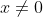 et et 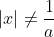 et et 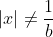
Et l'équation est équivalente à +b(\frac{1}{|x|}-a)+2(\frac{1}{|x|}-a)(\frac{1}{|x|}-b)}{(\frac{1}{|x|}-a)(\frac{1}{|x|}-b)}=0)
Ou encore à =0)
C'est-à-dire 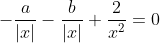
Ou bien }{x^2}=0)
Ainsi =2)
- Si a=-b ou a=b=0, alors manifestement, 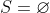
- Si 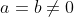 , alors , alors 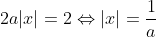 . Mais l'équation n'est pas définie dans ce cas, donc . Mais l'équation n'est pas définie dans ce cas, donc 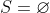
- Sinon, 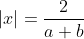 , et donc , et donc 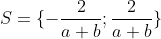
Synthèse :
- Si 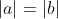 , alors , alors 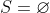
- Si 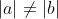 , alors , alors 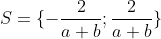 Je me corrige encore une fois, car je me suis trompé. La synthèse doit être la suivante : - Si 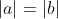 ou  , alors 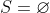 - Si 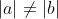 et  , alors 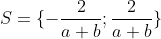 - Citation :
- Dijckashiener félicitation pour le 5/6
Ne disons pas 5/6 car je n'ai pas parfait le premier (je n'ai pas pris en considération toutes les conditions sur a et b), et j'ai un peu travaillé sur le cinquième. Merci tout de même. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Lun 17 Mai 2010, 15:36 Lun 17 Mai 2010, 15:36 | |
| Pour le cinquième: On veut démontrer que:  . Puisque l'exercice n'est pas du niveau, procédons avec récurrence. Pour n=1. On a  . On prend 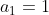 et 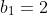 . On a donc  . Donc  . Donc  . Donc  . Pour n=2. On a  . On prend 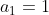 et 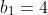 et 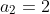 et 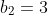 . On a donc  . Donc  . Donc  . Donc  . Ainsi  . Et  est juste pour ces deux cas. Montrons maintenant qu'elle est juste pour l'indicce n+1. On a démontré que  . Donc  . Et que  . Donc  . Donc  . Soit  . On pourra réaliser ce travail jusqu'a n, pour trouver finalement que  . D'autre part: On a -1) . Donc -1-1-...-1) . (les uns se répétent n+1 fois) Donc (n+2)}{2}-(n+1)) . Donc (n+2)-(n+1)) . Donc  . Donc  . Donc ^2) . CQFD. Sauf n'importe quelle sorte d'erreur. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Mar 18 Mai 2010, 20:32 Mar 18 Mai 2010, 20:32 | |
| - Dijkschneier a écrit:
- nmo a écrit:
A propos de l'exercice 5, les troncs communs n'ont pas encore étudier les ensemble.
On doit poser la question, pourquoi cet exercice est présent ici?
Mais bien sûr que si. Il suffit de connaître un peu ses cours pour s'en rendre compte.
- nmo a écrit:
En plus pour l'exercice 6:
Si je ne me trompe pas, pour montrer que trois droites sont concourantes en un seul point il faut choisir un triangle convenable, puis on démontre que ces droites ne sont autres que les médianes ou les bissectrices ou les médiatrice ou les hauteurs.
J'attends ton avis.
Dans des problèmes différents, cela peut évidemment être une approche possible. Mais si vous aviez eu le soin de construire la figure, vous en conviendrez que l'on ne peut se fixer un seul triangle intéressant dans lequel ces droites là seront des céviennes (médianes, hauteurs, médiatrices, ...), et de ce fait, le problème n'est pas abordable de la sorte. J'ai personnellement construit mon raisonnement en jouant avec l'analyse, c-à-d en commençant par construire un repère orthonormé centré sur le le centre du quadrilatère. J'ai ouï dire par un forumiste qu'on pouvait utiliser le produit scalaire, et cela me semble envisageable, également. Ni avec le produit scalaire, ni avec l'analyse, j'ai résolu cet exercice. Il serait gentil de ta part de me donner la réponse, ainsi que ton avis sur ma démonstration par récurrence. Et merci. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Mar 18 Mai 2010, 23:35 Mar 18 Mai 2010, 23:35 | |
| Pour le 6 que vous demandez Mr nmo:  On a: I le milieu de [AB], J le milieu de [AD] => (Vec)IJ=kBD, çela veut dire bien que: (IJ)//(BD) et (BD)_|_(IJ). Avec: P(I)=I' et: P(J)=J' et: P(c)=c.(1). Soit M (تقاطع) de (II') et (JJ'), (Angles)IMG=I'MJ' (deux angles opposé par la téte) de méme: AMI=I'MC et: AMJ=CMJ'.(A) IAG+IMJ=180° et: I'CJ'+I'MJ'=180° et (A) <=> IAJ=I'CJ' Ainsi pour les autres angles(regarde le petit dessin), et on trouve que: les triangles IAJ et I'CJ' semblables. (2) De (1) et (2) en résulte que: A dans ABCD lui oppose M dans AIMJ. On a: P(I)=I' , P(J)=J', P(c)=c et A--->M donc: AIJM et ABCD semblables. Aussi: (BD)//(IJ)//(IJ') [la projection conserve le parallélisme] On resulte donc que: (I'J')_|_(AC) et: (IJ)_|_(AC) et (BD)_|_(AC) Et: les quadrillateres AIMJ, ABCD et: MJ'CI' semblables. (B) (AIMJ)C(ABCD) et: (MJ'CI')C(ABCD) --> (C) De (B) et (C) en résulte donc que: (AC)//(AM), et puisque: [AM] et [AC] et [MC] des diagonales qui sont orthogonales avec l'autres diagonales de ces quadrillateres, donc: (AC)//(AM) strictement. On résulte enfin que: (AC) , (II') et: (IJ') se coupent en une point on l'a appelé M. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Mer 19 Mai 2010, 00:21 Mer 19 Mai 2010, 00:21 | |
| - Spoiler:
Ni avec le produit scalaire, ni avec l'analyse, j'ai résolu cet exercice.
Il serait gentil de ta part de me donner la réponse, ainsi que ton avis sur ma démonstration par récurrence.
Et merci.
Comment? vous voullez dire de la réccurence partir du coté qu'on veut démontré, et arriver à l'autre? En mathématiques, le raisonnement par récurrence est une forme de raisonnement visant à démontrer une propriété portant sur tous les entiers naturels. Le raisonnement par récurrence consiste à démontrer les points suivants : Une propriété est satisfaite par l'entier 0 ; Si cette propriété est satisfaite par un certain nombre entier naturel n, alors elle doit être satisfaite par son successeur, c'est-à-dire, le nombre entier n+1. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Jeu 20 Mai 2010, 14:50 Jeu 20 Mai 2010, 14:50 | |
| - M.Marjani a écrit:
- Spoiler:
Ni avec le produit scalaire, ni avec l'analyse, j'ai résolu cet exercice.
Il serait gentil de ta part de me donner la réponse, ainsi que ton avis sur ma démonstration par récurrence.
Et merci.
Comment? vous voullez dire de la réccurence partir du coté qu'on veut démontré, et arriver à l'autre?
En mathématiques, le raisonnement par récurrence est une forme de
raisonnement visant à démontrer une propriété portant sur tous les
entiers naturels. Le raisonnement par récurrence consiste à démontrer les
points suivants :
Une propriété est satisfaite par l'entier 0 ;
Si cette propriété est satisfaite par un certain nombre entier naturel n,
alors elle doit être satisfaite par son successeur, c'est-à-dire, le nombre
entier n+1. Pour un petit indice n donné. Pas forcément pour 0. Ici, on a obligatoirement, le plus petit indice est 1. Dans ma démonstration, j'ai ajouté l'indice 2 pour m'aider dans l'étape de calcul | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 21 Mai 2010, 10:58 Ven 21 Mai 2010, 10:58 | |
| - M.Marjani a écrit:
- Pour le 6 que vous demandez Mr nmo:

On a: I le milieu de [AB], J le milieu de [AD]
=> (Vec)IJ=kBD, çela veut dire bien que: (IJ)//(BD) et (BD)_|_(IJ).
Avec: P(I)=I' et: P(J)=J' et: P(c)=c.(1).
Soit M (تقاطع) de (II') et (JJ'), (Angles)IMG=I'MJ' (deux angles opposé par la téte) de méme: AMI=I'MC et: AMJ=CMJ'.(A)
IAG+IMJ=180° et: I'CJ'+I'MJ'=180° et (A) <=> IAJ=I'CJ'
Ainsi pour les autres angles(regarde le petit dessin), et on trouve que: les triangles IAJ et I'CJ'
semblables. (2)
De (1) et (2) en résulte que: A dans ABCD lui oppose M dans AIMJ.
On a: P(I)=I' , P(J)=J', P(c)=c et A--->M donc: AIJM et ABCD semblables.
Aussi: (BD)//(IJ)//(IJ') [la projection conserve le parallélisme]
On resulte donc que: (I'J')_|_(AC) et: (IJ)_|_(AC) et (BD)_|_(AC)
Et: les quadrillateres AIMJ, ABCD et: MJ'CI' semblables. (B)
(AIMJ)C(ABCD) et: (MJ'CI')C(ABCD) --> (C)
De (B) et (C) en résulte donc que: (AC)//(AM), et puisque: [AM] et [AC] et [MC] des diagonales qui sont orthogonales avec l'autres diagonales de ces quadrillateres, donc: (AC)//(AM) strictement.
On résulte enfin que: (AC) , (II') et: (IJ') se coupent en une point on l'a appelé M. Bien joué. C'est une très belle methode. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 21 Mai 2010, 13:28 Ven 21 Mai 2010, 13:28 | |
| - nmo a écrit:
Bien joué.
C'est une très belle methode. Je suis bien surpris que vous fussiez capable de lire sa démonstration bourbeuse. Permettez-moi seulement de vous dresser la liste de toutes ces imprécisions : 1. Le dessin est tout erroné, car I et J sont censés être des milieux. 2. (IJ)//(BD) et (BD)_|_(IJ). => ... 3. Avec: P(I)=I' et: P(J)=J' et: P(c)=c.(1). => Quel rapport ? 4. IAG+IMJ=180° => Pourquoi ? 5. etc.. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Ven 21 Mai 2010, 15:39 Ven 21 Mai 2010, 15:39 | |
| - Dijkschneier a écrit:
- nmo a écrit:
Bien joué.
C'est une très belle methode. Je suis bien surpris que vous fussiez capable de lire sa démonstration bourbeuse.
Permettez-moi seulement de vous dresser la liste de toutes ces imprécisions :
1. Le dessin est tout erroné, car I et J sont censés être des milieux.
2. (IJ)//(BD) et (BD)_|_(IJ). => ...
3. Avec: P(I)=I' et: P(J)=J' et: P(c)=c.(1). => Quel rapport ?
4. IAG+IMJ=180° => Pourquoi ?
5. etc.. 1/ Je t'invite à le désiner donc, je ne suis pas d'un expert en logiciel "Paint"  2/ Si t'as lu tout tu vas comprendre (on veut démontrer deux choses semblables). 3/ Méme chose [UP]. 4/ Méme chose [UP]. Etc.. ==> Méme chose [UP]. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Sam 22 Mai 2010, 14:08 Sam 22 Mai 2010, 14:08 | |
| - M.Marjani a écrit:
1/ Je t'invite à le désiner donc, je ne suis pas d'un expert en logiciel "Paint" 
2/ Si t'as lu tout tu vas comprendre (on veut démontrer deux choses semblables).
3/ Méme chose [UP].
4/ Méme chose [UP].
Etc.. ==> Méme chose [UP]. 1.  2. Justement, je ne peux pas lire, car c'est simplement illisible. 3. 4. 5. Merci d'être plus clair. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Sam 22 Mai 2010, 16:32 Sam 22 Mai 2010, 16:32 | |
| 2. (IJ)//(BD) et (BD)_|_(IJ). => ... Une petite faute de frappe, au lieu de dire (BD)_|_(IJ) il faut dire: (AC)_|_(IJ) [(Vec)IJ=kBD]
3.On va utiliser la projection pour démontrer que: AIJM et ABCD semblables.
4. On peut considérer ABCD un quadrilatére inscriptible! | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Mar 08 Juin 2010, 11:20 Mar 08 Juin 2010, 11:20 | |
| - Dijkschneier a écrit:
- nmo a écrit:
Bien joué.
C'est une très belle methode. Je suis bien surpris que vous fussiez capable de lire sa démonstration bourbeuse.
Permettez-moi seulement de vous dresser la liste de toutes ces imprécisions :
1. Le dessin est tout erroné, car I et J sont censés être des milieux.
2. (IJ)//(BD) et (BD)_|_(IJ). => ...
3. Avec: P(I)=I' et: P(J)=J' et: P(c)=c.(1). => Quel rapport ?
4. IAG+IMJ=180° => Pourquoi ?
5. etc.. Je me suis trompé en croyant que (I'J') serait parallèle à (IJ) de toute façon. Je vais présenter une solution en me basant sur le produit scalaire. (Sans Latex, car il ne fonctionne pas correctement). | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Mar 08 Juin 2010, 11:38 Mar 08 Juin 2010, 11:38 | |
| Une solution pour l'exercice de géométrie:
(Ce qui est en bleu est vecteur)
Soit E et F les points d'intersections respectifs de (IJ) et (AC) et de (BD) et (AC).
Calculons le produit scalaire BD.AM.
On a BD.AM=(BJ+JI+ID+DB)(AC+CM).
Donc BD.AM=BJ.AC+JI.AC+ID.AC+DB.AC+BJ.CM+JI.CM+ID.CM+DB.CM.==>(*)
Or, on a BJ.AC=-JB.AC.
Donc BJ.AC=-EF.AC.
Car E est le projeté orthogonal de J, F celui de B, sur (AC).
De même ID.AC=EF.AC.
Car E est le projeté orthogonal de I, F celui de D, sur (AC).
Et JI.AC=0 et DB.AC=0.
Car ils sont orthogonaux.
Remplaçons dans *, et après la simplification, on aboutit à BD.AM=BJ.CM+JI.CM+ID.CM+DB.CM..
Donc BD.AM=(BJ+JI+ID+DB).CM..
Donc BD.AM=(BI+IB).CM..
Donc BD.AM=0.CM..
Donc BD.AM=0.
Ce qui donne que (AM) est perpendiculaire à (BD).
Comme on a selon l'énoncé (AC) est perpendiculaire à (BD).
Il vien que (AC) et (AM) sont parallèle.
A étant un point commun, donc M fait partie de (AC).
CQFD.
J'attends votre avis. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Mar 08 Juin 2010, 13:20 Mar 08 Juin 2010, 13:20 | |
| - nmo a écrit:
- Dijkschneier a écrit:
- nmo a écrit:
Bien joué.
C'est une très belle methode. Je suis bien surpris que vous fussiez capable de lire sa démonstration bourbeuse.
Permettez-moi seulement de vous dresser la liste de toutes ces imprécisions :
1. Le dessin est tout erroné, car I et J sont censés être des milieux.
2. (IJ)//(BD) et (BD)_|_(IJ). => ...
3. Avec: P(I)=I' et: P(J)=J' et: P(c)=c.(1). => Quel rapport ?
4. IAG+IMJ=180° => Pourquoi ?
5. etc.. Je me suis trompé en croyant que (I'J') serait parallèle à (IJ) de toute façon.
Je vais présenter une solution en me basant sur le produit scalaire.
(Sans Latex, car il ne fonctionne pas correctement). Sans parler de ma methode, posez votre solution svp. Si t'as quelque chose ou t'as eu le vertige pose là. [n'oublie pas que j'était dans un Test Olympique sans consontration....(si tu souviens de mes paroles)] Et si j'avais du temps je vais poster une autre solution sous consontration.. Je vais lire ta methode. Bonne chance. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Mar 08 Juin 2010, 13:41 Mar 08 Juin 2010, 13:41 | |
| - nmo a écrit:
- Une solution pour l'exercice de géométrie:
(Ce qui est en bleu est vecteur)
Soit E et F les points d'intersections respectifs de (IJ) et (AC) et de (BD) et (AC).
Calculons le produit scalaire BD.AM.
On a BD.AM=(BJ+JI+ID+DB)(AC+CM).
Donc BD.AM=BJ.AC+JI.AC+ID.AC+DB.AC+BJ.CM+JI.CM+ID.CM+DB.CM.==>(*)
Or, on a BJ.AC=-JB.AC.
Donc BJ.AC=-EF.AC.
Car E est le projeté orthogonal de J, F celui de B, sur (AC).
De même ID.AC=EF.AC.
Car E est le projeté orthogonal de I, F celui de D, sur (AC).
Et JI.AC=0 et DB.AC=0.
Car ils sont orthogonaux.
Remplaçons dans *, et après la simplification, on aboutit à BD.AM=BJ.CM+JI.CM+ID.CM+DB.CM..
Donc BD.AM=(BJ+JI+ID+DB).CM..
Donc BD.AM=(BI+IB).CM..
Donc BD.AM=0.CM..
Donc BD.AM=0.
Ce qui donne que (AM) est perpendiculaire à (BD).
Comme on a selon l'énoncé (AC) est perpendiculaire à (BD).
Il vien que (AC) et (AM) sont parallèle.
A étant un point commun, donc M fait partie de (AC).
CQFD.
J'attends votre avis. Bonjour, '' On a BD.AM=(BJ+JI+ID+DB)(AC+CM). '' BJ+JI+ID+DB=0 non pas BD (T'as parti de BD=0 et tu termines par BD=0 donc le raisonement est faux et désolé.) | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Mar 08 Juin 2010, 14:17 Mar 08 Juin 2010, 14:17 | |
| - M.Marjani a écrit:
- nmo a écrit:
- Une solution pour l'exercice de géométrie:
(Ce qui est en bleu est vecteur)
Soit E et F les points d'intersections respectifs de (IJ) et (AC) et de (BD) et (AC).
Calculons le produit scalaire BD.AM.
On a BD.AM=(BJ+JI+ID+DB)(AC+CM).
Donc BD.AM=BJ.AC+JI.AC+ID.AC+DB.AC+BJ.CM+JI.CM+ID.CM+DB.CM.==>(*)
Or, on a BJ.AC=-JB.AC.
Donc BJ.AC=-EF.AC.
Car E est le projeté orthogonal de J, F celui de B, sur (AC).
De même ID.AC=EF.AC.
Car E est le projeté orthogonal de I, F celui de D, sur (AC).
Et JI.AC=0 et DB.AC=0.
Car ils sont orthogonaux.
Remplaçons dans *, et après la simplification, on aboutit à BD.AM=BJ.CM+JI.CM+ID.CM+DB.CM..
Donc BD.AM=(BJ+JI+ID+DB).CM..
Donc BD.AM=(BI+IB).CM..
Donc BD.AM=0.CM..
Donc BD.AM=0.
Ce qui donne que (AM) est perpendiculaire à (BD).
Comme on a selon l'énoncé (AC) est perpendiculaire à (BD).
Il vien que (AC) et (AM) sont parallèle.
A étant un point commun, donc M fait partie de (AC).
CQFD.
J'attends votre avis.
Bonjour,
'' On a BD.AM=(BJ+JI+ID+DB)(AC+CM). ''
BJ+JI+ID+DB=0 non pas BD (T'as parti de BD=0 et tu termines par BD=0 donc le raisonement est faux et désolé.) Oui, je n'ai pas fait attention. Je vais essayer plus tard. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  Mer 09 Juin 2010, 17:14 Mer 09 Juin 2010, 17:14 | |
| Voilà une deuxième tentative: Reportons le plan au repère ) . Déterminons les coordonnées des points présents dans la figure de Dijkschneier. On a  . Donc ) . Et  . Donc ) . Et  . Donc ) . B est un point de OD. Donc il existe un réel négatif m, tel que  . Donc ) . Posons de même ) . On a I le milieu de [AD]. Donc  et  . Donc  et  . Donc  et  . On écrit ) . Même démonstration pour obtenir ) . Soit ) le point d'intersection des droites perpendiculaires respectivement à (BC) et à (DC) et passant respectivement par les milieux de [AD] (c'est I) et [AB](c'est J). On a ) . Donc ) . Et de même ) . D'autre part, ) . Donc ) . Donc ) . Et de même ) . On a  est perpendiculaire à 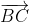 . Donc *(-m)+(\beta-\frac{1}{2})*(n)=0) . Donc  . Donc  . Donc  .==>(1) On a  est perpendiculaire à  . Donc *(1)+(\beta-\frac{1}{2})*(-n)=0) . Donc  . Donc  . Donc  .==>(2) De 1 et 2, on conclut que  . Donc  . Donc  . Donc  . Donc =0) . Donc 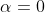 ou 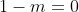 . Donc 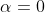 ou 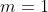 . Comme m est négatif, il vient que 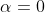 . Ce qui prouve que M appartient à l'axe des ordonnées, qui n'est autre que (AC). CQFD. J'espère cette fois-ci que ma solution est juste. A vous maintenant de juger. | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Olympiade de Kénitra (2nd tour) Sujet: Re: Olympiade de Kénitra (2nd tour)  | |
| |
|   | | | | Olympiade de Kénitra (2nd tour) |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
