| | Préparation pour le troisième tour d'olympiade: |  |
|
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Préparation pour le troisième tour d'olympiade: Sujet: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 20:03 Mer 28 Avr 2010, 20:03 | |
| - Idriss BOUDHAR a écrit:
- OLYMPIADES MATHEMATIQUES
Exercice 1
Soient x, et y deux réels tels que x>0 et y>0.
Soit m le plus petit des nombres x, 1/y et y+1/x.
Démontrer que m=<V2.
Exercice 2
Déterminer toutes les applications f de IR vers IR telles que pour tous x et
y de IR: f(x+y)*f(x-y)=2x+f(x^2-y^2).
Exercice 3
Démontrer que quelquesoit a:
a^2004 - a^2003 + a^1998 - a^1995 + a^1992 - a +1 > 0
Exercice 4
On construit à l’extérieur d’un triangle ABC les deux rectangles ABB1B2 et
ACC1C2 tels que : AB=AC2 et AC=AB2
Soit S le point d’intersection de (BC2) et (CB2)
1-démontrer que la mesure de BSC est 90°.
2-démontrer que B1, S et C1 sont alignés.
Exercice 5
Soit a un réel non nul. Sachant que a^3+18/a^3=18 calculer a^4+1/a^4.
Exercice 6
x, y et z sont des réels strictement positifs tels que xyz(x+y+z)=1
Démontrer que (x+y)(y+z)>=2.
Exercice 7
Soient x et y deux réels strictement positifs.
Démontrer que Vx(1+1/y)+Vy(1+1/x)>=4.
Exercice 8 (25-11-2005)
On pose :a_n=1/[(n+1)Vn+nV(n+1)].
Calculer a1+a2+a3+……+a99.
Exercice 9 (25-11-05)
a) u, v, x et y sont des nombres réels strictement positifs. Montrer que :u/x + v/y >= 4(uy+xv)/(x+y)^2.
b) a, b, c, et d sont des nombres réels strictement positifs. Montrer que: a/(b+2c+d)+ b/(c+2d+a) + c/(d+2a+b) + d/(a+2b+c)>=1.
Exercice 10 (25-11-05)
ABCD est quadrilatère convexe et inscriptible tel que CD<AB et BC<AD
soit P un point du segment [AB] tel que AP=CD et soit Q un point du
segment [AD] tel que AQ=BC. Les droites (AC) et (PQ) se coupent en M.
Montrer que M est le milieu de [PQ].
Exercice 11 (25-11-05)
Déterminer toutes les fonctions réelles f définies sur IR et vérifiant:
yf(2x)-xf(2y)=8xy(x^2-y^2).
Exercice 12 (11-11-05)
Soit ABCD un rectangle. Soient E et F deux points de la diagonale [AC]
tels que : AE=AB et AF=AD. Soient G et H respectivement les projections
orthogonales de E et F sur [AB]. Montrer que AG+FH=AC.
Exercice 13 (11-11-05)
Soient a, b et c trois réels strictement positifs tels que : abc=1
Montrer que :(1+ab)/1+a +(1+bc)/1+b + (1+ac)/1+c>=3.
Exercice 14 (11-11-05)
Déterminer tous les nombres naturels premiers p et q tel que (p+1)^q soit
un carré parfait. (i.e :carré d’un nombre naturel)
Exercice 15 (11-11-05)
Soient a, b et c trois réels tels que : |a|<1, |b|<1 et |c|<1.
Montrer que ab+cb+ca+1>0 Celui ou celle qui veut répondre doit citer l'exercice puis le résoudre. Un point pour une très bonne réponse pour voir qui sera notre gagnant pour ce petit jeu. Moi aussi, je vais participer car je viens de télécharger ce PDF. Que le défi se lance. Bonne chance.
Dernière édition par nmo le Jeu 29 Avr 2010, 08:42, édité 6 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 20:16 Mer 28 Avr 2010, 20:16 | |
| Les exercices 5, 6, et 15 sont annulés car ils sont déja postés.
Si celui qui va réondre ne veut pas citer, il doit numéroter l'exercice. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 20:31 Mer 28 Avr 2010, 20:31 | |
| Pour 1 c plutôt m=min(x,1/y,x+1/y)
Sinon prends x=y=1 ou x=1 ,y=2
Dernière édition par Sylphaen le Mer 28 Avr 2010, 20:33, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 20:31 Mer 28 Avr 2010, 20:31 | |
| Pour l'exercice 9: a: On a ^2\ge0) . Donc 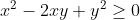 . Donc 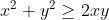 . Donc 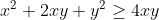 . Donc ^2\ge4xy) . Donc ^2}\le\frac{4}{xy}) . Donc \frac{4}{(x+y)^2}\le\frac{1}{xy}(uy+vx)) . Donc }{(x+y)^2}\le\frac{uy+vx}{xy}) . Donc }{(x+y)^2}\le\frac{uy}{xy}+\frac{xv}{xy}) . Donc }{(x+y)^2}\le\frac{u}{x}+\frac{v}{y}) . CQFD.
Dernière édition par nmo le Mer 28 Avr 2010, 20:34, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 20:33 Mer 28 Avr 2010, 20:33 | |
| - Sylphaen a écrit:
- Pour 1 c plutôt m=<2
Sinon prends x=y=1 ou x=1 ,y=2 Pour assurer ton intervention, réponds à la question. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 20:34 Mer 28 Avr 2010, 20:34 | |
| Bonjour, bien fais Mr nmo  J'ai pensé qu'il ya une faute. Mr Sylphaen mes doutes  Bonne remarque. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 20:52 Mer 28 Avr 2010, 20:52 | |
| J'ai édité ma remarque , et pour confirmer mes doutes : Si m=x alors : 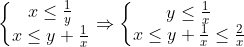 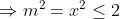 Si m=1/y alors : 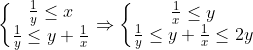 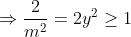 Si m=y+1/x alors : 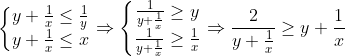 D'où le résultat . | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 21:02 Mer 28 Avr 2010, 21:02 | |
| Pour le 7: +\sqrt{y}(1+\frac{1}{x})) . Et on a \ge 2\frac{\sqrt{x}}{\sqrt{y}}) et \ge 2\frac{\sqrt{y}}{\sqrt{x}}) Donc +\sqrt{y}(1+\frac{1}{x}) \ge 2(\frac{\sqrt{y}}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{y}})) D'autre part =2) Finalement +\sqrt{y}(1+\frac{1}{x}) \ge 2(\frac{\sqrt{y}}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{y}})=2*2=4) CQFD
Dernière édition par louis le Jeu 29 Avr 2010, 07:26, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 21:22 Mer 28 Avr 2010, 21:22 | |
|
Dernière édition par M.Marjani le Jeu 29 Avr 2010, 17:43, édité 2 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 21:25 Mer 28 Avr 2010, 21:25 | |
| T'a commis une erreur fatal Marjani !
1+ab>1 et 1+a>1 n'implique pas que 1+ab/1+a>1
Car 1/a+1<1 .
Enfin pour celui là il suffit d'utiliser l'inégalité entre les moyenne et on a (1+ab)(1+ac)(1+bc)/(1+a)(1+b)(1+c)=1 .. | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 21:33 Mer 28 Avr 2010, 21:33 | |
|
Dernière édition par A446 le Jeu 29 Avr 2010, 18:38, édité 1 fois | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 21:34 Mer 28 Avr 2010, 21:34 | |
|
Dernière édition par A446 le Jeu 29 Avr 2010, 18:29, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 21:36 Mer 28 Avr 2010, 21:36 | |
| - Sylphaen a écrit:
- T'a commis une erreur fatal Marjani !
1+ab>1 et 1+a>1 n'implique pas que 1+ab/1+a>1
Car 1/a+1<1 .
Enfin pour celui là il suffit d'utiliser l'inégalité entre les moyenne et on a (1+ab)(1+ac)(1+bc)/(1+a)(1+b)(1+c)=1 .. Je t'invite à poster la solution complète pour mériter un point. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 21:39 Mer 28 Avr 2010, 21:39 | |
| - A446 a écrit:
- Pour le 3 c'est trop logique:
on a:
a^2004=(a^1002)^2>0
-a^2003 est toujour plus peti que a^2004 qui est strictement positif
donc:a^2004-a^2003>0
on fait la meme chose pour a^1998 et -a^1995
ce qui donne:
a^1998-a^1995>0
donc:
a^2004-a^2003+a^1998-a^1995>0
a^2004-a^2003+a^1998-a^1995+1>0
et encore on fait la meme technique avec -a et a^1992
ce qui donne la solution. Si 1>a. Donc a^2003>2^2004. au cas ou a est positif. Une solution fausse et pas logique. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 21:52 Mer 28 Avr 2010, 21:52 | |
| Pour le 2:
On a f(x+y)*f(x-y)=2x+f(x^2-y^2).
Donc f(x+y)*f(x-y)=x+y+x-y+f((x-y)(x+y)).
Posons a=x+y et b=x-y.
Alors f(a)*f(b)=a+b+f(ab).
Si a=b=0.
Alors f(0)*f(0)=0+0++f(0).
Donc f(0)*f(0)=f(0).
Donc f(0)*f(0)-f(0)=0.
Donc f(0)[f(0)-1]=0.
Donc f(0)=0 ou f(0)-1=0.
Donc f(0)=0 ou f(0)=1.
Le premier cas: f(0)=0.
On prend a=1 et b=0.
On a f(a)*f(b)=a+b+f(ab).
Donc f(1)*f(0)=1+0+f(0*1).
Donc 0*f(1)=1+f(0).
Donc 0=1+0.
Donc 0=1.
Ce qui est faux.
Le deuxième cas: f(0)=1.
On prend b=0.
On a f(a)*f(b)=a+b+f(ab).
Donc f(a)*f(0)=a+0+f(a*0).
Donc 1*f(a)=a+f(0).
Donc f(a)=a+1.
Réciproquement, soit a et b de IR.
On a f(a)*f(b)=(1+a)(1+b).
Donc f(a)*f(b)=1+a+b+ab.==>(1)
Et on a a+b+f(ab)=a+b+1+ab.==>(2)
De 1 et 2, on conclut que f(a)*f(b)=a+b+f(ab).
De tout qui précède, on conclut que la seule application qui vérifie les donnée est f(a)=1+a.
Bien entendu f(x)=1+x.
A vous de juger. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 22:08 Mer 28 Avr 2010, 22:08 | |
| - Sylphaen a écrit:
- T'a commis une erreur fatal Marjani !
1+ab>1 et 1+a>1 n'implique pas que 1+ab/1+a>1
Car 1/a+1<1 .
Enfin pour celui là il suffit d'utiliser l'inégalité entre les moyenne et on a (1+ab)(1+ac)(1+bc)/(1+a)(1+b)(1+c)=1 .. Désolé, j'ai pas compléter l'écriture de la démonstration, je veux pas dire ça xD. ---------------------------------------------------------------------------------- Bon voilà pour 2: f(x+y)*f(x-y)=2x+f(x²-y²) Prenons x=y: f(2x)*f(0)=2x+f(0) (2) => f(0).(f0-1)=0 => f(0)=0 Ou f(0)=1 Cas1: Si f(0)=0 on a: f(0).(f(2)-1)=0 Mais dans la premiére égalité prenons x=y=1 donc on a: f(0).(f(2)-1)=2 (3) Ce qui est impossible. Cas2: Si f(0)=1 On a: dans (2) f(2x)-1=2x=> f(2x)=2x+1 (4) Et dans (3) : f(2)=3 Donc: prenons x=1 dans (4) On trouve que: f(2)=3 ! Ce qui est vrai. On suppose (عسكيا) alors que: f(0)=1 Et prenons f(x+y)*f(x-y)=2x+f((x+y)(x-y)=f(X)*(Y)=f(XY)+X+Y car:((x+y)+(x-y)=2x=X+Y) Et prenons X=0 => f(0)*f(Y)=f(0)+Y =>f(y)=Y+1 D'ou f(x)=x+1 Ammicalement ^^ | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 22:20 Mer 28 Avr 2010, 22:20 | |
| - nmo a écrit:
- Pour le 2:
A vous de juger. Bien fais, desolé j'ai pas copié ta methode, on a fait l'exercise en méme temps. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 22:40 Mer 28 Avr 2010, 22:40 | |
| Une petite édite dans ma méthode, pour la rendre complétement différente de Mr nmo  Bon voilà pour 2: f(x+y)*f(x-y)=2x+f(x²-y²) Prenons x=y: f(2x)*f(0)=2x+f(0) (2) => f(0).(f0-1)=0 => f(0)=0 Ou f(0)=1 Cas1: Si f(0)=0 on a: f(0).(f(2)-1)=0 Mais dans la premiére égalité prenons x=y=1 donc on a: f(0).(f(2)-1)=2 (3) Ce qui est impossible. Cas2: Si f(0)=1 On a: dans (2) f(2x)-1=2x=> f(2x)=2x+1 (4) Et dans (3) : f(2)=3 Donc: prenons x=1 dans (4) On trouve que: f(2)=3 ! Ce qui est vrai. On suppose (عسكيا) alors que: f(0)=1 Et prenons dans la fonction: f(2x)=2x+1 : 2x=x D'ou la seule fonction qui est juste dans |R est: f(x)=x+1 Ammicalement ^^ | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Mer 28 Avr 2010, 22:58 Mer 28 Avr 2010, 22:58 | |
| Je suis trés fatigué ce jour. A demain ncha2 lah. Laissez-moi un EX, car je sais que vous allez les finir cette nuit xD Bonne chance.  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Jeu 29 Avr 2010, 09:05 Jeu 29 Avr 2010, 09:05 | |
| Pour le 8: On a \sqrt{n}+n\sqrt{n+1}}) . Donc \sqrt{n}-n\sqrt{n+1}}{((n+1)\sqrt{n}+n\sqrt{n+1})((n+1)\sqrt{n}-n\sqrt{n+1})}) . Donc \sqrt{n}-n\sqrt{n+1}}{((n+1)\sqrt{n})^2-(n\sqrt{n+1})^2}) . Donc \sqrt{n}-n\sqrt{n+1}}{n(n+1)^2-(n+1)n^2}) . Donc \sqrt{n}-n\sqrt{n+1}}{n(n+1)(n+1-n)}) . Donc \sqrt{n}-n\sqrt{n+1}}{n(n+1)}) . Donc 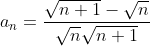 . Donc 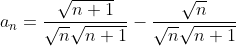 . Donc 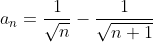 . Si n=1, alors 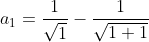 . Donc 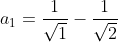 . Si n=2, alors 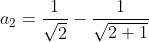 . Donc 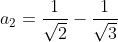 . Et .... Si n=99, alors 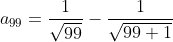 . Donc 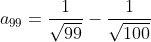 . En sommant, on trouve 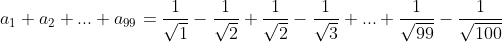 . Donc 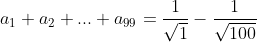 . Donc 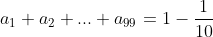 . Donc 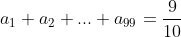 . J'espère que ça soit juste. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Jeu 29 Avr 2010, 17:39 Jeu 29 Avr 2010, 17:39 | |
|
Dernière édition par M.Marjani le Jeu 29 Avr 2010, 18:07, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Jeu 29 Avr 2010, 17:49 Jeu 29 Avr 2010, 17:49 | |
| nmo: 2.5 pts M.Marjani:2 pts Sylphaen:1 pts Louis: 1pts En attendant de vos participation. Au plaisir  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Jeu 29 Avr 2010, 18:45 Jeu 29 Avr 2010, 18:45 | |
| Pour l'éxercise 3  Posons: 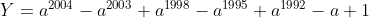 Si: 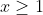 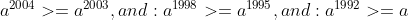 On a: 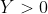 Si: 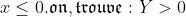 (car le tout est positif,il ya le carré et -a=x'£|R+) Si: 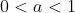 Là on peut faire une petite variation: Donc posons: 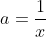 Et puisque 0<a<1: il en résulte que: x>1 On peut écrire Y sous forme: +\frac{1}{x^{2004}}+\frac{1}{x^{1998}}+\frac{1}{x^{1992}}+1) On a: 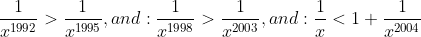 Ou bien: 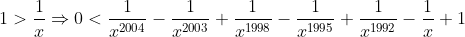 D'ou: Y>0 dans |R CQFD  Et j'espére que c'est juste. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 12:41 Ven 30 Avr 2010, 12:41 | |
| Bonjour  Pour le 14: Premiére cas: p et q sont des nombres naturels premiérs tel que: (p+1)^q soit un carré parfait d'un nombre naturel biensur. ^q=a^2\Leftrightarrow P=a-1,and:q=2) Premier) Et: 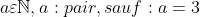 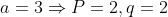 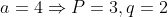 . . . 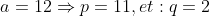 /k:Tout,nombre,impair\varepsilon \mathbb{N} \right \}) 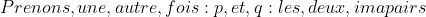 2éme cas: ^q=a^2) 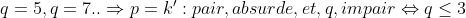 Exemple de ce que je veux dire par le 2éme cas: q=7=> Il faut que: p+1=7 pour que: (p+1)^q=a'^2 =>p=6 Il faut que p+1 soit pair de tout q£N*-{1,2,3}, puisque:P impair d'aprés les donnés. On a: P pair de tout x>3. Ce qui est absurde. Donc 2=<q=<3  ;(p=k;q=2)/k:Tout,nombre,impair\varepsilon \mathbb{N} \right \}) CQFD.
Dernière édition par M.Marjani le Ven 30 Avr 2010, 13:47, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 14:19 Ven 30 Avr 2010, 14:19 | |
| Pour le premier j'ai vu que m est le plus petit de x+1/y et y+1/x. Et qu'on doit montré que m=<2 à la place de m=<V2  Donc: les donnés sont changés. Je vais le faire dans une feuile une autre fois malgré il est déja répondu. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  | |
| |
|
  | |
| | Préparation pour le troisième tour d'olympiade: |  |
|
