| | Préparation pour le troisième tour d'olympiade: |  |
|
|
|
| Auteur | Message |
|---|
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 17:16 Ven 30 Avr 2010, 17:16 | |
| *pour le septième: (1-Vy)²>=0
alors: 1+(1/y)>=2/Vy
d'ou: Vx(1+1/y)>=2Vx/Vy
de la même façon :Vy(1+1/x)>=2Vy/Vx
donc: Vx(1+1/y)+Vy(1+1/x)>=(2x+2y)/V(xy)
et puisque: (2x+2y-4V(xy))/V(xy)=(2(Vx-Vy)²)/V(xy)
alors: (2x+2y)/V(xy)-4>=0
donc: (2x+2y)/Vxy>=4
ce qui implique: Vx(1+1/y)+Vy(1+1/x)>=4
*pour le douzième:
On a : ABCD un rectangle et E et G appartiennent respectivement à [AC]et [AB]
Et: (EG)L(AB)
Alors,selon le théo de Thales,on a :AG/AB=AE/AC
alors: AG=(AE*AB)/AC
et puisque:AE=AB
alors: AG=AB²/AC
de la meme façon,on obtiendra: FH=BC²/AC
AG+FH=(AB²+AC²)/AC
puisque:ABC est un triangle rectangle en B
alors: AB²+BC²=AC²
on obtient: AG+FH=AC²/AC=AC
Sauf erreur | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 18:16 Ven 30 Avr 2010, 18:16 | |
| Pour le 4:
Après avoir dessiné la bonne figure,
On a ACC1C2 un carré.
Donc AC2=AC.
Et on a AC2=AB.
Donc AC=AB.==>(1)
De la même manière, on prouve que: AB2=AC2.==>(2)
On a CAC2=BAB2=90°. (angles)
Donc CAC2+CAB=BAB2+CAB. (angles)
Donc C2AB=B2AC. (angles)==>(3)
De 1, 2, et 3, il résulte que les triangles C2AB et CAB2 sont isométriques.
Donc les mesures de leurs angles juxtaposés sont égaux.
Donc ABC2=ACB2. (angles)==>(4)
D'autre part, on a AB2=AC.
Donc le triangle ACB2 est isocèle en A.
Donc ACB2=AB2C. (angles)==>(5)
De 4 et 5, on conclut que ABC2=AB2C.
Soit en réalité ABS=AB2S.
Donc le quadrilatère AB2BS est inscriptible.
On a B2SB=BAB2 (angles) car ils sont deux angles interceptant le même arc [B2B].
Comme BAB2 est un carré, BAB2=90°. (angle)
Enfin BSB2=90°. (angle)
On a C, S, et B2 des points allignés.
Donc CSB2=180°. (angle)
Donc CSB+BSB2=180°. (angles)
Donc CSB+90°=180°. (angle)
Donc CSB=90°. (angle)
Ce qu'il fallait démonterer en un premier temps.
On a CSB+BSB2=180°. (angles)
Donc CSB+BSB1+B1SB2=180°. (angles)
Et puisque B2SB1=C1SC (angles) car ils sont juxtaposés à tête.
Donc CSB+C1SC+B1SB2=180°. (angles)
Donc C1SB1=180°. (angle)
Donc les points C1, S, et B1 sont allignés.
Ce qu'il fallait démonterer en un second temps.
CQFD. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 18:29 Ven 30 Avr 2010, 18:29 | |
| - W.Elluizi a écrit:
- *pour le septième: (1-Vy)²>=0
alors: 1+(1/y)>=2/Vy
d'ou: Vx(1+1/y)>=2Vx/Vy
de la même façon :Vy(1+1/x)>=2Vy/Vx
donc: Vx(1+1/y)+Vy(1+1/x)>=(2x+2y)/V(xy)
et puisque: (2x+2y-4V(xy))/V(xy)=(2(Vx-Vy)²)/V(xy)
alors: (2x+2y)/V(xy)-4>=0
donc: (2x+2y)/Vxy>=4
ce qui implique: Vx(1+1/y)+Vy(1+1/x)>=4
*pour le douzième:
On a : ABCD un rectangle et E et G appartiennent respectivement à [AC]et [AB]
Et: (EG)L(AB)
Alors,selon le théo de Thales,on a :AG/AB=AE/AC
alors: AG=(AE*AB)/AC
et puisque:AE=AB
alors: AG=AB²/AC
de la meme façon,on obtiendra: FH=BC²/AC
AG+FH=(AB²+AC²)/AC
puisque:ABC est un triangle rectangle en B
alors: AB²+BC²=AC²
on obtient: AG+FH=AC²/AC=AC
Sauf erreur Bien joué. Tu veux dire de AG+FH=(AB²+AC²)/AC, AG+FH=(BC²+AB²)/AC, faute de frappe  En attendant de vos participation avec vos propres methodes des exercises non faites. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:10 Ven 30 Avr 2010, 19:10 | |
| - M.Marjani a écrit:
- Bonjour

Pour le 14:
Premiére cas:
p et q sont des nombres naturels premiérs tel que: (p+1)^q soit un carré parfait d'un nombre naturel biensur.
^q=a^2\Leftrightarrow P=a-1,and:q=2)
Premier) Et: Et: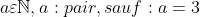
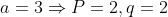
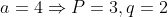
.
.
.
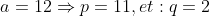
/k:Tout,nombre,impair\varepsilon \mathbb{N} \right \})
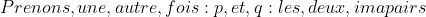
2éme cas:
^q=a^2)
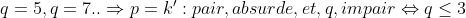
Exemple de ce que je veux dire par le 2éme cas:
q=7=> Il faut que: p+1=7 pour que: (p+1)^q=a'^2 =>p=6
Il faut que p+1 soit pair de tout q£N*-{1,2,3}, puisque:P impair d'aprés les donnés.
On a: P pair de tout x>3. Ce qui est absurde. Donc 2=<q=<3
 ;(p=k;q=2)/k:Tout,nombre,impair\varepsilon \mathbb{N} \right \})
CQFD. En fait, il y a une partie qui est juste, o.5 point pour l'effort. p est un entier quelquonque et q=2. 2 est bien sûr premier. L'autre cas est où q#2. Donc q est impair. Dans ce cas c'est p+1 qui est un carré parfait. Posons p+1=a^2. Donc p=a^2-1. Donc p=(a-1)(a+1). Les diviseurs de p sont p et 1 avec p>=2. On sait que a+1>=a-1. Donc p=a+1 et 1=a-1. Donc a=2 et p=2+1. Donc p=3. 2 est bien sûr premier. Ce sont les deux cas possibles. Amicalement. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:14 Ven 30 Avr 2010, 19:14 | |
| - M.Marjani a écrit:
- nmo: 2.5 pts
M.Marjani:2 pts
Sylphaen:1 pts
Louis: 1pts
En attendant de vos participation.
Au plaisir  Maintenant, on a: M.Marjani:3.5 pts. nmo: 3.5 pts. Sylphaen:1 pt. Louis: 1pt. E.Elluizi: 1pt. Bonne chance, le jeu n'est pas encore terminé. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:15 Ven 30 Avr 2010, 19:15 | |
| [quote="nmo"] - M.Marjani a écrit:
- Bonjour

Pour le 14:
Amicalement. Non mais il faut citer ou est la faute svp, car je vois nettement qu'il n'y a aucune faute. Si tu n'as pas compris quelques choses, dis moi.  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:20 Ven 30 Avr 2010, 19:20 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:23 Ven 30 Avr 2010, 19:23 | |
| [quote="M.Marjani"] - nmo a écrit:
- M.Marjani a écrit:
- Bonjour

Pour le 14:
Amicalement.
Non mais il faut citer ou est la faute svp, car je vois nettement qu'il n'y a aucune faute. Si tu n'as pas compris quelques choses, dis moi.  Ce que je veux dire que si p=3, alors: p+1=4=2^2. Et (p+1)^q=(2^2)^q. Donc (p+1)^q=(2^q)^2. Qui est un carré parfait, pas forcément q=3 ce que tu as trouvé. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:25 Ven 30 Avr 2010, 19:25 | |
| [quote="M.Marjani"][quote="nmo"] - M.Marjani a écrit:
- Bonjour

Pour le 14:
En fait, il y a une partie qui est juste, o.5 point pour l'effort.
p est un entier quelquonque et q=2.
2 est bien sûr premier.
L'autre cas est où q#2.
Donc q est impair.
Dans ce cas c'est p+1 qui est un carré parfait.
Posons p+1=a^2.
Donc p=a^2-1.
Donc p=(a-1)(a+1).
Les diviseurs de p sont p et 1 avec p>=2.
On sait que a+1>=a-1.
Donc p=a+1 et 1=a-1.
Donc a=2 et p=2+1.
Donc p=3.
2 est bien sûr premier.
Ce sont les deux cas possibles.
Amicalement. Oui, dans le deuxiéme cas p+1=a'², c'est ça ce que je veux dire, si t'as regarder bien ma réponse tu vas remarquer que: p+1=a'²  quote] | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:26 Ven 30 Avr 2010, 19:26 | |
| On a p#2 car on a déja étudier ce cas, taa première démonstratio.
Ensuite 0 n'est pas premier, ainsi que 1
Donc p>2.
Dernière édition par nmo le Ven 30 Avr 2010, 19:27, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:27 Ven 30 Avr 2010, 19:27 | |
| [quote="nmo"] - M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- Bonjour

Pour le 14:
Amicalement.
Non mais il faut citer ou est la faute svp, car je vois nettement qu'il n'y a aucune faute. Si tu n'as pas compris quelques choses, dis moi.  Ce que je veux dire que si p=3, alors: p+1=4=2^2.
Et (p+1)^q=(2^2)^q.
Donc (p+1)^q=(2^q)^2.
Qui est un carré parfait, pas forcément q=3 ce que tu as trouvé. Si, si Mr, q=3 et p=3 sont les solutions dans le cas ou q=3, et q=3 est un cas particulier si t'as bien vu ma réponse. Sinon donne moi un contre exemple.
Dernière édition par M.Marjani le Ven 30 Avr 2010, 19:34, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:30 Ven 30 Avr 2010, 19:30 | |
| - nmo a écrit:
- On a p#2 car on a déja étudier ce cas, taa première démonstratio.
Ensuite 0 n'est pas premier, ainsi que 1
Donc p>2. Oui, tu sais que sin on continue de ce que t'as dis dans le deuxiéme cas, on vas trouver que les solutions impair q,p: seront q=3, et p=3 puisque p+1=a'² <=> 2=<q=<3, car on va trouver P pair de tout p>3 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:35 Ven 30 Avr 2010, 19:35 | |
| M.Marjani, tu as fait un effort honorable.
C'est pour cela que tu mérites 0.5 point, même si la démonstration n'est pas rigoureuse, et laisse les autres critiquer.
Passons à un autre exercice.
Il ne reste que trois exercices avant la fin.
Bonne chance. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:39 Ven 30 Avr 2010, 19:39 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:41 Ven 30 Avr 2010, 19:41 | |
| [quote="nmo"] - M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- Bonjour

Pour le 14:
Amicalement.
Non mais il faut citer ou est la faute svp, car je vois nettement qu'il n'y a aucune faute. Si tu n'as pas compris quelques choses, dis moi.  Ce que je veux dire que si p=3, alors: p+1=4=2^2.
Et (p+1)^q=(2^2)^q.
Donc (p+1)^q=(2^q)^2.
Qui est un carré parfait, pas forcément q=3 ce que tu as trouvé. Regarde bien que q peut avoir 3, 5, 7, 9, ... un premier quelquesoit. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:52 Ven 30 Avr 2010, 19:52 | |
| [quote="nmo"] - nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- Bonjour

Pour le 14:
Amicalement.
Non mais il faut citer ou est la faute svp, car je vois nettement qu'il n'y a aucune faute. Si tu n'as pas compris quelques choses, dis moi.  Ce que je veux dire que si p=3, alors: p+1=4=2^2.
Et (p+1)^q=(2^2)^q.
Donc (p+1)^q=(2^q)^2.
Qui est un carré parfait, pas forcément q=3 ce que tu as trouvé. Regarde bien que q peut avoir 3, 5, 7, 9, ... un premier quelquesoit. Oui, j'ai citer ça.. mais vu que P est pair dans le deuxiéme cas quand q est premier de tout q>3. C'est pourquoi j'ai dis que q=3 et q=2 sont les seules nombres premiers qui sont des solutions. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 19:56 Ven 30 Avr 2010, 19:56 | |
| [quote="M.Marjani"] - nmo a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- Bonjour

Pour le 14:
Amicalement.
Non mais il faut citer ou est la faute svp, car je vois nettement qu'il n'y a aucune faute. Si tu n'as pas compris quelques choses, dis moi.  Ce que je veux dire que si p=3, alors: p+1=4=2^2.
Et (p+1)^q=(2^2)^q.
Donc (p+1)^q=(2^q)^2.
Qui est un carré parfait, pas forcément q=3 ce que tu as trouvé. Regarde bien que q peut avoir 3, 5, 7, 9, ... un premier quelquesoit.
Oui, j'ai citer ça.. mais vu que P est pair dans le deuxiéme cas quand q est premier de tout q>3. C'est pourquoi j'ai dis que q=3 et q=2 sont les seules nombres premiers qui sont des solutions. Maintenant, on est d'accord ou pas encore? | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 20:01 Ven 30 Avr 2010, 20:01 | |
| [quote="nmo"] - M.Marjani a écrit:
- nmo a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- Bonjour

Pour le 14:
Amicalement.
Non mais il faut citer ou est la faute svp, car je vois nettement qu'il n'y a aucune faute. Si tu n'as pas compris quelques choses, dis moi.  Ce que je veux dire que si p=3, alors: p+1=4=2^2.
Et (p+1)^q=(2^2)^q.
Donc (p+1)^q=(2^q)^2.
Qui est un carré parfait, pas forcément q=3 ce que tu as trouvé. Regarde bien que q peut avoir 3, 5, 7, 9, ... un premier quelquesoit.
Oui, j'ai citer ça.. mais vu que P est pair dans le deuxiéme cas quand q est premier de tout q>3. C'est pourquoi j'ai dis que q=3 et q=2 sont les seules nombres premiers qui sont des solutions. Maintenant, on est d'accord ou pas encore? No  Car ta méthode qui consiste à: p+1=a'² dans le deuxiéme cas, c'est comme p+1=q, tout les deux donne a'²  Donne moi un contre exemple qui prouve que les solutions que j'ai trouvé sont fausses. Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 20:06 Ven 30 Avr 2010, 20:06 | |
| [quote="M.Marjani"] - nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- Bonjour

Pour le 14:
Amicalement.
Non mais il faut citer ou est la faute svp, car je vois nettement qu'il n'y a aucune faute. Si tu n'as pas compris quelques choses, dis moi.  Ce que je veux dire que si p=3, alors: p+1=4=2^2.
Et (p+1)^q=(2^2)^q.
Donc (p+1)^q=(2^q)^2.
Qui est un carré parfait, pas forcément q=3 ce que tu as trouvé. Regarde bien que q peut avoir 3, 5, 7, 9, ... un premier quelquesoit.
Oui, j'ai citer ça.. mais vu que P est pair dans le deuxiéme cas quand q est premier de tout q>3. C'est pourquoi j'ai dis que q=3 et q=2 sont les seules nombres premiers qui sont des solutions. Maintenant, on est d'accord ou pas encore?
No 
Car ta méthode qui consiste à: p+1=a'² dans le deuxiéme cas, c'est comme p+1=q, tout les deux donne a'² 
Donne moi un contre exemple qui prouve que les solutions que j'ai trouvé sont fausses.
Bonne chance. Elle ne sont pas fausses, mais ils ne sont pas complètes. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Ven 30 Avr 2010, 20:23 Ven 30 Avr 2010, 20:23 | |
| - nmo a écrit:
Bonne chance. Elle ne sont pas fausses, mais ils ne sont pas complètes.[/quote] Okey, c'est ton avis alors. )) Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Sam 01 Mai 2010, 16:41 Sam 01 Mai 2010, 16:41 | |
| Pour le 11:
On veut déterminer toutes les applications f de IR vers IR telles que pour tous x et y de IR yf(2x)-xf(2y)=8xy(x^2-y^2).
On prend pour cela x=(1/2)a et y=(1/2)b.
On a yf(2x)-xf(2y)=8xy(x^2-y^2).
Donc (1/2)b*f(2*1/2*a)-(1/2)a*f(2*1/2*b)=8*b*1/2*a*1/2*b*((1/2)a)^2-((1/2)b)^2).
Donc (1/2)[b*f(a)-a*f(b)]=2ab*((1/4)a^2-(1/4)b^2).
Donc b*f(a)-a*f(b)=4ab*(1/4)(a^2-b^2).
Donc bf(a)-af(b)=ab(a^2-b^2).
Prenons a=2 et b=1.
On a bf(a)-af(b)=ab(a^2-b^2).
Donc 1f(2)-2f(1)=2*1*(2^2-1^2).
Donc 1f(2)-2f(1)=2*1*(4-1).
Donc f(2)-2f(1)=2*3.
Donc f(2)-2f(1)=6.
Donc f(2)=6+2f(1).==>(1)
Prenons a=3 et b=1.
On a bf(a)-af(b)=ab(a^2-b^2).
Donc 1f(3)-3f(1)=3*1*(3^2-1^2).
Donc f(3)-3f(1)=3*(9-1).
Donc f(3)-3f(1)=3*8.
Donc f(3)-3f(1)=24.
Donc f(3)=24+3f(1).==>(2)
Prenons a=3 et b=2.
On a bf(a)-af(b)=ab(a^2-b^2).
Donc 2f(3)-3f(2)=2*3*(3^2-2^2).
Donc 2f(3)-3f(2)=6*(9-4).
Donc 2f(3)-3f(2)=6*5.
Donc 2f(3)-3f(2)=30.
Donc 2f(3)=30+3f(2).==>(3)
Prenons a=4 et b=1.
On a bf(a)-af(b)=ab(a^2-b^2).
Donc 1f(4)-4f(1)=4*1*(4^2-1^2).
Donc f(4)-4f(1)=4*(16-1).
Donc f(4)-4f(1)=4*15.
Donc f(4)-4f(1)=60.
Donc f(4)=60+4f(1).==>(4)
Prenons a=4 et b=1.
On a bf(a)-af(b)=ab(a^2-b^2).
Donc 2f(4)-4f(2)=4*2*(4^2-2^2).
Donc 2f(4)-4f(2)=8*(16-4).
Donc 2f(4)-4f(2)=8*12.
Donc 2f(4)-4f(2)=96.
Donc 2f(4)=96+4f(2).
Donc f(4)=48+2f(2).==>(5)
Prenons a=4 et b=3.
On a bf(a)-af(b)=ab(a^2-b^2).
Donc 3f(4)-4f(3)=4*3*(4^2-3^2).
Donc 3f(4)-4f(3)=12*(16-9).
Donc 3f(4)-4f(3)=12*7.
Donc 3f(4)-4f(3)=84.
Donc 3f(4)=84+4f(3).==>(6)
De 1, 2, 3, 4, 5, et 6 on résoud le système composés des équations suivantes:
f(2)=6+2f(1).
f(3)=24+3f(1).
2f(3)=30+3f(2).
f(4)=60+4f(1).
f(4)=48+2f(2).
3f(4)=84+4f(3).
On pose f(1)=m, f(2)=n, f(3)=p, et f(4)=q.
Le système devient:
n=6+2m.
p=24+3m.
2m=30+3n.
q=60+4m.
q=48+2n.
3q=84+4p.
La résolution de ce système donne clairement:
m=6, n=18, p=42, et q=84.
Soit f(1)=6.
Prenons b=1.
On a bf(a)-af(b)=ab(a^2-b^2).
Donc 1f(a)-af(1)=a*1(a^2-1^2).
Donc f(a)-a*6=a(a^2-1).
Donc f(a)-6a=a^3-a.
Donc f(a)=a^3+5a.
Même résultat trouvé en remplaçant par les autres nombres.
Réciproquement, soit f une application qui vérifie: f(a)=a^3+5a.
On a f(2x)=(2x)^3+5*2x.
Donc f(2x)=8x^3+10x.
Donc yf(2x)=8yx^3+10xy.
De même -xf(2y)=8xy^3+10xy.
Donc yf(2x)-xf(2y)=8yx^3+10xy-(8xy^3+10xy).
Donc yf(2x)-xf(2y)=8yx^3+10xy-8xy^3-10xy.
Donc yf(2x)-xf(2y)=8yx^3-8xy^3.
Donc yf(2x)-xf(2y)=8xy(x^2-y^2).
On conclut que la seule application qui satisfait l'énoncé est f(a)=a^3+5a.
Bien entendu f(x)=x^3+5x.
A vous de juger.
Dernière édition par nmo le Sam 01 Mai 2010, 20:15, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Sam 01 Mai 2010, 16:42 Sam 01 Mai 2010, 16:42 | |
| On discute à propos des solutions du système dans l'autre topic.
Merci pour la compréhension. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Sam 01 Mai 2010, 18:26 Sam 01 Mai 2010, 18:26 | |
| Après la résolution du système, je rectifie mon message.
Je ne sais pas pourquoi, mais la fonction que j'ai trouvé est juste. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Sam 01 Mai 2010, 19:03 Sam 01 Mai 2010, 19:03 | |
| - nmo a écrit:
- Après la résolution du système, je rectifie mon message.
Je ne sais pas pourquoi, mais la fonction que j'ai trouvé est juste. C'est faux le systéme mr nmo )) Bonne chance à toi. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  Sam 01 Mai 2010, 19:23 Sam 01 Mai 2010, 19:23 | |
| - M.Marjani a écrit:
- nmo a écrit:
- Après la résolution du système, je rectifie mon message.
Je ne sais pas pourquoi, mais la fonction que j'ai trouvé est juste.
C'est faux le systéme mr nmo ))
Bonne chance à toi. Y-a-t-il une faute à laquelle je n'ai pas fait attention? | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation pour le troisième tour d'olympiade: Sujet: Re: Préparation pour le troisième tour d'olympiade:  | |
| |
|
  | |
| | Préparation pour le troisième tour d'olympiade: |  |
|
