Défi:

Montrez que le nombre n'est pas un entier.
Bonne chance.

Essayez avec ces deux exercices:
1/https://mathsmaroc.jeun.fr/seconde-tronc-commun-f6/exo-olympiade-tc-9-t5638.htm.
2/https://mathsmaroc.jeun.fr/seconde-tronc-commun-f6/exo3-olympiade-t1860.htm.
Bonne chance.

Bonjourno

On a:
(Remarquer que: n² cotient 20 chiffres !)
On sait que: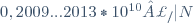
Car: 0,2009...2013*10^{10}=2009201020.1120122013 n'apartient pas à |N !!!
0,2009...2013 n'apartient pas à |N => V0,2009...2013*10^10 n'apartient pas à |N !!!
=>
D'ou: n£_/|N.
(£_/: veut dire n'appartient pas).
CQFD.

Ta solution Est fausse !
V0.25 n'appartient pas à N
mais 2V0.25 appartient à N ..
Sinon montrer qu'aucun carré ne peut se terminé avec un 3 ..

Mr Sylphaen;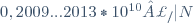

Car: 0,2009...2013*10^{10}=2009201020.1120122013 n'apartient pas à |N !!!
0,2009...2013 n'apartient pas à |N => V0,2009...2013*10^10 n'apartient pas à |N !!!

Autre methode:
Vous pouvez montrez que: xyznt (xyznt nombre, tel que: x,y,z,n,t 5 nombres succésive) n'est jamais un carré parfait.
et déduisant que: le nombre (2009 2010 2011 2012 2013) n'est pas un carré parfait.

Sylphaen a écrit:

Ta solution Est fausse !
V0.25 n'appartient pas à N
mais 2V0.25 appartient à N ..
Sinon montrer qu'aucun carré ne peut se terminé avec un 3 ..

Si t'as bien vu, tu vas remarquer que j'ai remplaçer 0.2009...2013 qui n'appartient pas à |N par V0.2009...2013 (n'ppartient pas à |N aussi ) !
On sait que: 0.2009...2013*10^10 N'appartient pas à |N.(car: 2009...2013 contient 20 chiffres!)
Donc: V(0.2009...2013)*10^10 N'appartient pas à |N...

Sylphaen a écrit:

Ta solution Est fausse !
V0.25 n'appartient pas à N
mais 2V0.25 appartient à N ..
Sinon montrer qu'aucun carré ne peut se terminé avec un 3 ..

C'est la meilleure methode.
Continue.
Pour M.Marjani:
On a 0.589 n'apprtient pas à IN.
Que dites vous de (0.0589)^10?

oO Tu veux dire (0.0589)^{-10} ?
Car: 0.0589>(0.0589)^10=n^10 [0<n<1] est forcément n'appartient pas à |N !

--------------------------------------------------------------------------

Si t'as bien vu, tu vas remarquer que j'ai remplaçer 0.2009...2013 qui n'appartient pas à |N par V0.2009...2013 (n'ppartient pas à |N aussi ) !
On sait que: 0.2009...2013*10^10 N'appartient pas à |N.(car: 2009...2013 contient 20 chiffres!)
Donc: V(0.2009...2013)*10^10 N'appartient pas à |N...

M.Marjani a écrit:

oO Tu veux dire (0.0589)^{-10} ?
Car: 0.0589>(0.0589)^10=n^10 [0<n<1] est forcément n'appartient pas à |N !
--------------------------------------------------------------------------
Si t'as bien vu, tu vas remarquer que j'ai remplaçer 0.2009...2013 qui n'appartient pas à |N par V0.2009...2013 (n'ppartient pas à |N aussi ) !
On sait que: 0.2009...2013*10^10 N'appartient pas à |N.(car: 2009...2013 contient 20 chiffres!)
Donc: V(0.2009...2013)*10^10 N'appartient pas à |N...

La solution que tu présentes ici n'est pas bien structurée et enyueuse contrairement à celle de sylphaen qui est fort logique.
Rapelle-toi de la citation:
Cherchez l'autre solution juste.
Au plaisir.

louis a écrit:

M.Marjani a écrit:

oO Tu veux dire (0.0589)^{-10} ?
Car: 0.0589>(0.0589)^10=n^10 [0<n<1] est forcément n'appartient pas à |N !
--------------------------------------------------------------------------
Si t'as bien vu, tu vas remarquer que j'ai remplaçer 0.2009...2013 qui n'appartient pas à |N par V0.2009...2013 (n'ppartient pas à |N aussi ) !
On sait que: 0.2009...2013*10^10 N'appartient pas à |N.(car: 2009...2013 contient 20 chiffres!)
Donc: V(0.2009...2013)*10^10 N'appartient pas à |N...

La solution que tu présentes ici n'est pas bien structurée et enyueuse contrairement à celle de sylphaen qui est fort logique.
Rapelle-toi de la citation:
Cherchez l'autre solution juste.
Au plaisir.

C'est ça ce que je voulais dire.
Il reste encore les autres exercices qui sont d'un très haut niveau.

Pour l'exo où il y'a la surface l'énoncé est faux ca doit être inférieur ou égal pas supérieur ou égal ..
Juste utiliser le fait que :
S(ABCD)=S(ABD)+S(BCD)
=1/2( AB.AD sinD + BC.CD sinC ) ..

Pour le 2éme qui est trés difficile


On sait que: TQy=180°-OQT
=> TQy=2QMT+PMQ-OQT
=> TQy=2QMT+180°-(2TPQ+MPQ)-OQT
On sait que: 180°-OQT= TQy => TQy-TQy=2QMT-2TPQ-MQP
=> 2QMT-2TPQ-MQP=0 (1)
On voit que les deux triangles OPT et OMQ ont tous les deux le quadrilatére OMRP et se ressemble en MOP (OMRP serait un quadrilatére inscriptible). Considéron une cercle qui entoure les points M,T,P,Q:
Donc on a: MTP=MQP <=> TMR=QPR=OMP
Etd'aprés (1) on a: MQP=0°
MQP=0° <=> MPQ=180° => MPO=180°
Cela veut dire bien que: M£(Oy) (1)
De (1) et par M£(Oy) on résulte que: Ox==Oy (منطبقان)
La bissectrice de MPy recoupe Ox en T, ça veut dire donc que: [PT)==[QT). (A)
[PT) bissectrice de MPQ=180°, d'ou: [PT)_|_(Oy)
Donc: QT est bissectrice de MQy=180°.

CQFD.

Edité !

M.Marjani a écrit:

Pour le 2éme qui est trés difficile

On sait que: TQy=180°-OQT
=> TQy=2QMT+PMQ-OQT
=> TQy=2QMT+180°-2TPQ+MPQ-OQT
On sait que: 180°-OQT= TQy => TQy-TQy=2QMT-2TPQ+MQP
=> 2QMT-2TPQ+MQP=0
Déduisant le systéme suivant:

=> MQP=0° <=> MPQ=180° => MPO=180°
Cela veut dire bien que: M=Q (منطبقان) (1)
De (1) et par M£(Oy) on résulte que: Ox==Oy (منطبقان)
La bissectrice de MPy recoupe Ox en T, ça veut dire donc que: [PT)==[QT). (A)
[PT) bissectrice de MPQ=180°, d'ou: [PT)_|_(Oy)
Donc: QT est bissectrice de MQy=180°.

Je ne suis pas de ton avis.
Tu n'as qu'à observer la figure.

nmo

Il ya une faute dans la figure (au lieu de faire Ox j'ai fais Oy), mais la démonstration reste juste
La figure est edité.

Montrez que le nombre r acinr 20092010201120122013 n'est pas un entier.


Sylphaen a dit :

Sinon montrer qu'aucun carré ne peut se terminé avec un 3 .
voici une solution : on sait que le reste de division par 10 d'un entier c'est le ciffre d'unité.
En faisant une étude des restes de division de n2 par 10, on constate que le nombre 3 ne figure pas parmis ces restes.

Sylphaen a écrit:

Pour l'exo où il y'a la surface l'énoncé est faux ca doit être inférieur ou égal pas supérieur ou égal ..
Juste utiliser le fait que :
S(ABCD)=S(ABD)+S(BCD)
=1/2( AB.AD sinD + BC.CD sinC ) ..

Ce qui est en rouge est juste.
Je poste ma solution plus tard.

dhiab a écrit:

Montrez que le nombre r acinr 20092010201120122013 n'est pas un entier.


Sylphaen a dit :

Sinon montrer qu'aucun carré ne peut se terminé avec un 3 .
voici une solution : on sait que le reste de division par 10 d'un entier c'est le ciffre d'unité.
En faisant une étude des restes de division de n2 par 10, on constate que le nombre 3 ne figure pas parmis ces restes.

Une methode de tronc commun:
Soit A un entier naturel.
Si A avait dans les nombres d'unités 1,
Alors A² aurait 1.
Si A avait dans les nombres d'unités 2,
Alors A² aurait 4.
Si A avait dans les nombres d'unités 3,
Alors A² aurait 9
Si A avait dans les nombres d'unités 4,
Alors A² aurait 6 (4²=16)
Si A avait dans les nombres d'unités 5,
Alors A² aurait 5 (5²=25)
Si A avait dans les nombres d'unités 6,
Alors A² aurait 6 (6²=36)
Si A avait dans les nombres d'unités 7,
Alors A² aurait 9 (7²=49)
Si A avait dans les nombres d'unités 8,
Alors A² aurait 4 (8²=64)
Si A avait dans les nombres d'unités 9,
Alors A² aurait 1 (9²=81)
Aucun de ces carrées ne se termine par 3.
Donc V(20092010201120122013) n'est pas un entier.
Au plaisir.

Bien. Mais c'est ca ce qu'a fais Mr Dhiab dans son tableau --'

M.Marjani a écrit:

Bien. Mais c'est ca ce qu'a fais Mr Dhiab dans son tableau --'

J'ai écrit cette methode car les troncs commun n'ont pas encore fait les modulos.