| | question de symétrie |  |
|
|
| Auteur | Message |
|---|
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: question de symétrie Sujet: question de symétrie  Jeu 24 Juin 2010, 00:34 Jeu 24 Juin 2010, 00:34 | |
| Exo :
ABCD : un rectangle ( AB = 4 , AD= 6 )
R un point de [AB] , AR = x
T un point de [AD] , AT = y
A' le symétrique de A par rapport à (RT).
Condition sur x ,y pour que A' soit sur [BC].
----------------------------------------------------------------
| |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Jeu 24 Juin 2010, 17:17 Jeu 24 Juin 2010, 17:17 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Jeu 24 Juin 2010, 17:37 Jeu 24 Juin 2010, 17:37 | |
|  ? | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Jeu 24 Juin 2010, 22:56 Jeu 24 Juin 2010, 22:56 | |
|
salam
c'est presque....
y = x.rac( 2 /(x-2) )
.....................................
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Ven 25 Juin 2010, 14:16 Ven 25 Juin 2010, 14:16 | |
| Tout à fait. Et l'on arrive bien à montrer que (A' est sur [BC]) => (y = x*rac(2/(x-2)) ), mais dans le sens inverse, c'est un peu plus rude. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Sam 26 Juin 2010, 10:49 Sam 26 Juin 2010, 10:49 | |
| - houssa a écrit:
salam
c'est presque....
y = x.rac( 2 /(x-2) )
..................................... Soit I un point de [AB] et J un point de [AD]. Tel que AI=AJ=1. Le plan est donc muni d'un repère cartésien orthonormé ) . Pour ne pas avoir des illusion, posons AR=a et AT=b. On calcule les coordonnée de chaque point, on trouve que ) , ) , ) , ) , ) , ) , ) , et ) . Il faut trouver la condition sur a et b pour que A' soit sur [BC]. On a (BC) une droite parallèle à l'axe des ordonnées, passant par ) . Donc : x=4) . On a A' fait partie de (BC). Donc 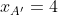 . Soit M le milieu de [AA']. On a 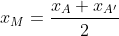 . Donc 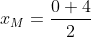 . Donc  . Donc 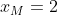 .==>(1) Ecrivons les équations réduites des deux droites (TR) et (AA'). On a ) et ) . Et on a :\frac{x-x_R}{y-y_R}=\frac{x_T-x_R}{y_T-y_R}) . Donc :\frac{x-a}{y-0}=\frac{0-a}{b-0}) . Donc :\frac{x-a}{y}=-\frac{a}{b}) . Donc :(x-a)b=-ay) . Donc :xb-ab=-ay) . Donc :ab-xb=ay) . Donc :y=\frac{ab-xb}{a}) . Donc :y=\frac{ab}{a}-\frac{xb}{a}) . Donc :y=-\frac{b}{a}x+b) est une équation réduite de la droite (TR). Et on a A' le symétrique de A par rapport à (RT). Donc (AA') est perpendiculaire à (RT). Donc le produit de leur coéfficients directeurs égale -1. Donc le coéfficient directeur de (AA') est 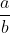 . Et puis que l'origine appartient à (AA'), on écrit :y=\frac{a}{b}x) . On a ) est l'intersection de (AA') et (RT). Donc les coordonnées de M vérifient le système 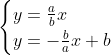 . Résolvons-le. On a 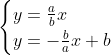 . Donc 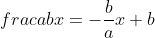 . Donc 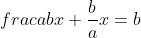 . Donc x=b) . Donc 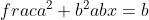 . Donc x=ab^2) . Donc 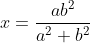 .==>(2) De 1 et 2, on déduit que 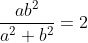 . Donc 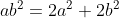 . Donc 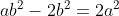 . Donc =2a^2) . Donc }{2}) . Donc }{2}}) . Donc 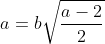 . Ou 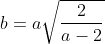 . P.S: Je sais que rien n'est affiché. Je vous prie d'attendre que le latex soit réparé. (Je réflichis pour le réciproque plus tard). | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Dim 27 Juin 2010, 09:15 Dim 27 Juin 2010, 09:15 | |
| Bonjour; Pourquoi toujours: y = x.rac( 2 /(x-2) )  On peut trouver une autre relation entre x et y. -------------------------------------------------------------------------- - Spoiler:
On a: Cos(TDB)=6/V52. TDB=TAC. BD=V52. TA'=x
Avec: TA'²=TB²-y²=TC²-(6-y)²
Dans le triangle TAC on applique al cachy: TC²=y²+52-2V(52)*y*Cos(TAC)=y²+52-2V(52)*y*6/V52=y²+52-12y
Puisque dans le triangle TDC: TC²=TD²+x²=(6-y)²+x²
Cela veut dire forcément que: x=4 et A'£[BC].
Deuxiéme methode:
On a:y=6-TD .
x²=52-(y+TD)²=52-y²-2y*(6-y)-(6-y)²=52-y²-12y+2y²-y²-36+12y=16
=> x=4
On résulte donc que: quelle que soit y de [AD] avec x=4, on aura A'£[BC].
Dernière édition par M.Marjani le Dim 27 Juin 2010, 14:20, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Dim 27 Juin 2010, 09:34 Dim 27 Juin 2010, 09:34 | |
| Ou bien:
y²=x²+BT²-2x*BT*Cos(ABT)=BT²-x² ; avec: Cos(ABT)=x/BT
=> y²=2x²+y²-2x*V(x²+y²)*cos(ABT)
=> Cos(ABT)=2x(V(x²+y²)-x)
Cos(ABT)=2x(V(x²+y²)-4)=x/BT=x/V(x²+y²)
=> 2(V(x²+y²)-4)=1/V(x²+y²)
=> 2(x²+y²)-8V(x²+y²)=1
Posant V(x²+y²)=X: 2X²-8X-1=0
Delta=72 , X=(8-V72)/2 (Impossible) ou Bien: X=(8+V72)/2
=> V(x²+y²)=(8+V72)/2
=> x²+y²=(8+V72)²/4
Merci.
Dernière édition par M.Marjani le Dim 27 Juin 2010, 21:37, édité 1 fois | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Dim 27 Juin 2010, 12:55 Dim 27 Juin 2010, 12:55 | |
| salam marjani
y² = x² + BT² - 2.x.BT .cos(ABT) ?????????????
attention x = AR
. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Dim 27 Juin 2010, 13:15 Dim 27 Juin 2010, 13:15 | |
| Désolé Mr Houssam pour le premier poste, il ya du vertige là.
Pour le deuxiéme poste:
A' le symétrique de A par rapport à RT, donc ARA'T est rectangle.
Et on a: A'£[BC] ==(ABCD rectangle)==> TA'=AB=x=4 => RB=0 et AT=y=cte ,B==R.
Ca veux dire on suppose pour trouver la relation. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Dim 27 Juin 2010, 15:08 Dim 27 Juin 2010, 15:08 | |
| salam :
ARA'T est rectangle ???????
.....................TA' = AB = x ??????????
.vous êtes sûr de votre dessin ???? | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Dim 27 Juin 2010, 19:45 Dim 27 Juin 2010, 19:45 | |
| - houssa a écrit:
- salam :
ARA'T est rectangle ???????
.vous êtes sûr de votre dessin ???? Pourquoi non? [AR]£[AB] et: [AT]£[AD] [AB] _|_ [AD] => [AR] _|_ [AT] A' le symtrique de A par raport à [RT] cela veut dire que: ... | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Dim 27 Juin 2010, 22:51 Dim 27 Juin 2010, 22:51 | |
| salam
< : veut dire angle
------------------------------
sur la figure :
<RAT = 90°
<RA'T = 90°
et les autres ??? d'où vient le rectangle ARA'T .?
............................... | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  Lun 28 Juin 2010, 10:54 Lun 28 Juin 2010, 10:54 | |
| - Dijkschneier a écrit:
- Tout à fait. Et l'on arrive bien à montrer que (A' est sur [BC]) => (y = x*rac(2/(x-2)) ), mais dans le sens inverse, c'est un peu plus rude.
Je respecte ce point de vue, mais en utilisant l'analyse cela se rend très facile. Au plaisir. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: question de symétrie Sujet: Re: question de symétrie  | |
| |
|
  | |
| | question de symétrie |  |
|
