|
| | Exo |  |
|
+7darkpseudo master Dijkschneier nmo M.Marjani -Crash- Azerty1995 11 participants | |
| Auteur | Message |
|---|
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Exo Sujet: Re: Exo  Dim 22 Aoû 2010, 16:48 Dim 22 Aoû 2010, 16:48 | |
| - nmo a écrit:
- Dijkschneier a écrit:
- Si on met tous les termes du RHS au même dénominateur, il vient (a+b+c)n² + (3a+2b+c)n + 2a = 1. Egalité de polynômes, donc on a le système constitué des trois égalités : a+b+c=0, 3a+2b+c=0 et 2a = 1. Le triplet solution est (1/2,-1,1/2).
Une telle décomposition s'appelle une décomposition en éléments simples, et c'est vraiment un exercice pour exercer ses connaissances sur les polynômes.
Pour en savoir plus : [url=http://fr.wikipedia.org/wiki/D%C3%A9composition_en_%C3%A9l%C3%A9ments_simples http://fr.wikipedia.org/wiki/D%C3%A9composition_en_%C3%A9l%C3%A9ments_simples[/quote[/url]]
Excellent, il existe une autre solution plus longue, elle se base sur les cours étudiés au collège.
Je te promet de la poster si personne ne le fait. Souvent, ce genre d'exercises, admet toujours un seul triplet, tu peux l'inspirer vitement d'une seule réflixion. Pour cette exercise, peut étre résolu comme suit: (n+2)}=\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n(n+2)}) (n+2)}=\frac{1}{2n}-\frac{1}{n+1}-\frac{1}{2(n+2)}) Voiçi une application: Voiçi une application:On veut calculer par exemple: 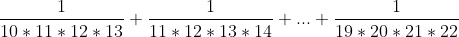 Une solution crée par moi: Une solution crée par moi:On veut démontrer l'égalité suivante: (n+2)(n+3)}=-\frac{1}{2(n+1)}+\frac{1}{2(n+2)}-\frac{1}{6(n+3)}+\frac{1}{6n}\\\Leftrightarrow%20\frac{1}{n(n+1)(n+2)(n+3)}=\frac{1}{2}\begin{pmatrix}%20-\frac{1}{n+1}+\frac{1}{n+2}%20\end{pmatrix}+\frac{1}{6}\begin{pmatrix}%20-\frac{1}{n+3}+\frac{1}{n}%20\end{pmatrix}) On a: (n+2)}-\frac{1}{(n+1)(n+2)(n+3)})) Or : (n+2)}=\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n(n+2)}) (n+2)}=\frac{1}{2n}-\frac{1}{n+1}-\frac{1}{2(n+2)}) 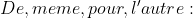 Il suffit de remarquer que: n devient n+1. (n+2)(n+3)}=\frac{1}{2(n+1)}-\frac{1}{n+2}-\frac{1}{2(n+3)}) }-\frac{1}{n+1}-(\frac{1}{2(n+1)}-\frac{1}{n+2}-\frac{1}{2(n+3)}))) }+\frac{1}{6(n+3)}-\frac{1}{2(n+1)}) Cela est un cas géneraliser pour calculer d'autres formules qui semblent à notre application. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Mer 25 Aoû 2010, 22:05 Mer 25 Aoû 2010, 22:05 | |
| - M.Marjani a écrit:
- nmo a écrit:
- Dijkschneier a écrit:
- Si on met tous les termes du RHS au même dénominateur, il vient (a+b+c)n² + (3a+2b+c)n + 2a = 1. Egalité de polynômes, donc on a le système constitué des trois égalités : a+b+c=0, 3a+2b+c=0 et 2a = 1. Le triplet solution est (1/2,-1,1/2).
Une telle décomposition s'appelle une décomposition en éléments simples, et c'est vraiment un exercice pour exercer ses connaissances sur les polynômes.
Pour en savoir plus : [url=http://fr.wikipedia.org/wiki/D%C3%A9composition_en_%C3%A9l%C3%A9ments_simples http://fr.wikipedia.org/wiki/D%C3%A9composition_en_%C3%A9l%C3%A9ments_simples[/quote[/url]]
Excellent, il existe une autre solution plus longue, elle se base sur les cours étudiés au collège.
Je te promet de la poster si personne ne le fait. Souvent, ce genre d'exercises, admet toujours un seul triplet, tu peux l'inspirer vitement d'une seule réflixion.
Pour cette exercise, peut étre résolu comme suit:
(n+2)}=\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n(n+2)}) (n+2)}=\frac{1}{2n}-\frac{1}{n+1}-\frac{1}{2(n+2)})
Voiçi une application:
On veut calculer par exemple: 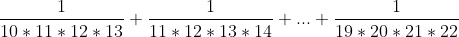
Une solution crée par moi:
On veut démontrer l'égalité suivante:
(n+2)(n+3)}=-\frac{1}{2(n+1)}+\frac{1}{2(n+2)}-\frac{1}{6(n+3)}+\frac{1}{6n}\\\Leftrightarrow%20\frac{1}{n(n+1)(n+2)(n+3)}=\frac{1}{2}\begin{pmatrix}%20-\frac{1}{n+1}+\frac{1}{n+2}%20\end{pmatrix}+\frac{1}{6}\begin{pmatrix}%20-\frac{1}{n+3}+\frac{1}{n}%20\end{pmatrix})
On a: (n+2)}-\frac{1}{(n+1)(n+2)(n+3)}))
Or : (n+2)}=\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n(n+2)}) (n+2)}=\frac{1}{2n}-\frac{1}{n+1}-\frac{1}{2(n+2)})
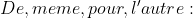 Il suffit de remarquer que: n devient n+1. Il suffit de remarquer que: n devient n+1.
(n+2)(n+3)}=\frac{1}{2(n+1)}-\frac{1}{n+2}-\frac{1}{2(n+3)})
}-\frac{1}{n+1}-(\frac{1}{2(n+1)}-\frac{1}{n+2}-\frac{1}{2(n+3)})))
}+\frac{1}{6(n+3)}-\frac{1}{2(n+1)})
Cela est un cas géneraliser pour calculer d'autres formules qui semblent à notre application. Le problème que tu as proposé n'a rien à avoir avec l'exercice que j'ai donné. En fait, il s'agit d'un ancien problème que j'ai proposé. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Mer 25 Aoû 2010, 22:28 Mer 25 Aoû 2010, 22:28 | |
| - nmo a écrit:
- Et pour enrichir un peu ce jeu, je propose:
Trouvez les réels a, b, et c tel que:
 . .
Bonne chance. Une réponse pour les collégiens, profitant de ce peu de temps. On a (n+2)}=\frac{a}{n}+\frac{b}{n+1}+\frac{c}{n+2}) . Pour n=1, il vient que (1+2)}=\frac{a}{1}+\frac{b}{1+1}+\frac{c}{1+2}) . Donc 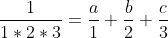 . Donc 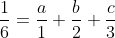 . Donc 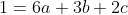 . Pour n=2, on trouve que 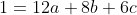 . Et pour n=3, on trouve que 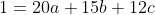 . On est ramené donc à la résolution du système 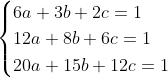 . Facilement, \}) . Au plaisir. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Exo Sujet: Re: Exo  Mer 25 Aoû 2010, 22:43 Mer 25 Aoû 2010, 22:43 | |
| - nmo a écrit:
- nmo a écrit:
- Et pour enrichir un peu ce jeu, je propose:
Trouvez les réels a, b, et c tel que:
 . .
Bonne chance. Une réponse pour les collégiens, profitant de ce peu de temps.
On a (n+2)}=\frac{a}{n}+\frac{b}{n+1}+\frac{c}{n+2}) . .
Pour n=1, il vient que (1+2)}=\frac{a}{1}+\frac{b}{1+1}+\frac{c}{1+2}) . .
Donc 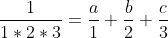 . .
Donc 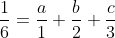 . .
Donc 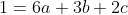 . .
Pour n=2, on trouve que 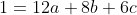 . .
Et pour n=3, on trouve que 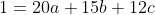 . .
On est ramené donc à la résolution du système 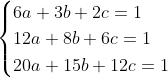 . .
Facilement, \}) . .
Au plaisir. Que direz vous du couple: (1,-1,-1/n)  (n+2)}=\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n(n+2)}) C'est pourquoi j'ai voullu posté mon dernier message, il fallait le lire avec plaisir nmo ^^ | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Ven 27 Aoû 2010, 16:37 Ven 27 Aoû 2010, 16:37 | |
| - M.Marjani a écrit:
- Que direz vous du couple: (1,-1,-1/n)

(n+2)}=\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n(n+2)})
C'est pourquoi j'ai voullu posté mon dernier message, il fallait le lire avec plaisir nmo ^^ Ce couple ne vérifie point le système. Je te rapelle qu'il s'agit d'un système à trois inconnus, à trois équations. Donc, il admet une solution unique qui est S={(1/2,-1,1/2)}. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Exo Sujet: Re: Exo  Ven 27 Aoû 2010, 17:18 Ven 27 Aoû 2010, 17:18 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Que direz vous du couple: (1,-1,-1/n)

(n+2)}=\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n(n+2)})
C'est pourquoi j'ai voullu posté mon dernier message, il fallait le lire avec plaisir nmo ^^ Ce couple ne vérifie point le système.
Je te rapelle qu'il s'agit d'un système à trois inconnus, à trois équations.
Donc, il admet une solution unique qui est S={(1/2,-1,1/2)}. Awdi lah Yhdik Tu veux dire plutot l'equation  ? ? Car le systéme est crée par toi, mais malheureusement il ne contient pas toutes les solutions.. ^^ Le couple (1,-1,-1/n) vérifie bien l'équation , nmo : ) C'est pourquoi je suis avec l'idée de Dijkschneier: Celà n'ecessite des connaissances sur les polynomes. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Ven 27 Aoû 2010, 18:28 Ven 27 Aoû 2010, 18:28 | |
| - M.Marjani a écrit:
Que direz vous du couple: (1,-1,-1/n) 
En effet, il marche aussi. Mais a, b et c sont implicitement définies comme étant des constantes. Or ici, c=-1/n est variable en fonction de n. Si on se foutait du fait que a, b et c sont des constantes, on prendrait ce triplet, aussi. Mais j'imagine que dans ce cas, il y aurait une infinité de tels triplets. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 | |   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Sam 28 Aoû 2010, 16:59 Sam 28 Aoû 2010, 16:59 | |
| - M.Marjani a écrit:
- Dijkschneier a écrit:
- M.Marjani a écrit:
Que direz vous du couple: (1,-1,-1/n) 
Si on se foutait du fait que a, b et c sont des constantes, on prendrait ce triplet, aussi. Mais j'imagine que dans ce cas, il y aurait une infinité de tels triplets. Exactement.  Certes. Hier, je n'ai pas bien calculer car j'étais préssé. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Sam 28 Aoû 2010, 17:54 Sam 28 Aoû 2010, 17:54 | |
| - nmo a écrit:
- J'ajoute un autre exercice:
a, b, et c sont les mesures des côtés d'un triangle ABC.
Démontrez que ab+bc+ca=<a²+b²+c²=<2(ab+bc+ca).
Bonne chance. On a 0=<(x-y)². Donc 0=<x²+y²-2xy. Donc 2xy=<x²+y². Posons x=a et y=b, il vient que a²+b²>=2ab.==>(1) Et de même b²+c²>=2bc.==>(2) Et aussi c²+a²>=2ca.==>(3) En sommant 1, 2, et 3, on trouve que a²+b²+b²+c²+c²+a²>=2ab+2bc+2ca. Donc 2a²+2b²+2c²>=2ab+2bc+2ca. Donc a²+b²+c²>=ab+bc+ca.==>(a) On a a, b et c sont les mesures des côtés d'un triangles. Donc (b-c)²=<a². Donc b²+c²-2bc=<a². Donc b²+c²=<a²+2bc.==>(4) De même c²+a²=<b²+2ac.==>(5) Et aussi a²+b²=<c²+2ab.==>(6) En sommant 4, 5, et 6, on trouve que a²+b²+b²+c²+c²+a²=<a²+b²+c²+2ab+2bc+2ca. Donc a²+b²+c²=<2ab+2bc+2ca. Donc a²+b²+c²=<2(ab+bc+ca).==>(b) De a et b, il s'ensuit que ab+bc+ca=<a²+b²+c²=<2(ab+bc+ca). CQFD. P.S: le but dde cet exercice est d'utiliser le fait que si a, b, et c sont le smesures des côtés d'un triangle, Alors (b-c)²=<a² et (c-a)²=<b² et (a-b)²=<c². | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Sam 28 Aoû 2010, 17:57 Sam 28 Aoû 2010, 17:57 | |
| - nmo a écrit:
- Un autre exercice:
ABC est un triangle rectangle en A.
[AH] est sa hauteur.
[AD) est la bissectrice intérieure de l'angle BAH.
[AE) celle de l'angle CAH.
Tel que D et E appartiennent à (BC).
Démontrez que AB+AC=BC+DE.
Bonne chance. Une réponse est dans ma prochaine visite si je ne trouve aucune. P.S: C'est un exercice de la deuxième année du collège. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Exo Sujet: Re: Exo  Sam 28 Aoû 2010, 18:10 Sam 28 Aoû 2010, 18:10 | |
| - nmo a écrit:
- J'ajoute un autre exercice:
a, b, et c sont les mesures des côtés d'un triangle ABC.
Démontrez que ab+bc+ca=<a²+b²+c²=<2(ab+bc+ca).
Bonne chance. Deuxiéme methode:ab+bc+ca=<a²+b²+c² : a²+b²>=2ab ; b²+c²>=2bc ; a²+c²>=2ac. Et en sommant 2(a²+b²+c²)>=2(ab+bc+ac) a²+b²+c²=<2(ab+bc+ca) <=> (a²-2ab)+(b²-2bc)+(c²-2ac)=<0 <=> (a(a-2b))+(b(b-2c))+(c(c-a))=<0 Ce qui est vrai car en supposant a>=b>=c
Dernière édition par M.Marjani le Sam 28 Aoû 2010, 18:19, édité 1 fois | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Sam 28 Aoû 2010, 18:14 Sam 28 Aoû 2010, 18:14 | |
| - M.Marjani a écrit:
- nmo a écrit:
- J'ajoute un autre exercice:
a, b, et c sont les mesures des côtés d'un triangle ABC.
Démontrez que ab+bc+ca=<a²+b²+c²=<2(ab+bc+ca).
Bonne chance.
Deuxiéme methode:
ab+bc+ca=<a²+b²+c² : a²+b²>=2ab ; b²+c²>=2bc ; a²+c²>=2ac. Et en sommant 2(a²+b²+c²)>=2(ab+bc+ac)
a²+b²+c²=<2(ab+bc+ca) <=> (a²-2ab)+(b²-2bc)+(c²-2ac)=<0 <=> (a(a-2b))+(b(b-2c))+(c(c-a))=<0
Ce qui est vrai car: La somme de deux cotés d'un triangle est superieur d'une cotée de ce dernier. Je ne pense pas. Exemple a=5 et b=1 et c=4.5 . Du fait a-2b est positif. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Sam 28 Aoû 2010, 18:27 Sam 28 Aoû 2010, 18:27 | |
| J'ajoute cet exercice: x, y, et z sont des réels vérifiant 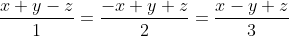 . Calculez 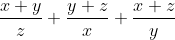 . Bonne chance. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Sam 28 Aoû 2010, 18:46 Sam 28 Aoû 2010, 18:46 | |
| Il semblerait qu'il n'y ait pas de collégiens par ici, nmo. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Exo Sujet: Re: Exo  Sam 28 Aoû 2010, 19:00 Sam 28 Aoû 2010, 19:00 | |
| - nmo a écrit:
Je ne pense pas.
Exemple a=5 et b=1 et c=4.5 .
Du fait a-2b est positif. - Spoiler:
Madich 3lya, rani sayam : )
Inégalité crée par moi: (a,b,c) des réels postives tel que 1=<c=<2, donc démontrez que: (a+b+c)² >= 2c(bc+ac)+4ab =< 4(ab+bc+ac)Autre déducations: (a,b,c) les cotés d'un triangle. Démontrer que : a+b+c =< 2V(ab+bc+ac) | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Lun 30 Aoû 2010, 17:36 Lun 30 Aoû 2010, 17:36 | |
| - nmo a écrit:
- nmo a écrit:
- Un autre exercice:
ABC est un triangle rectangle en A.
[AH] est sa hauteur.
[AD) est la bissectrice intérieure de l'angle BAH.
[AE) celle de l'angle CAH.
Tel que D et E appartiennent à (BC).
Démontrez que AB+AC=BC+DE.
Bonne chance. Une réponse est dans ma prochaine visite si je ne trouve aucune.
P.S: C'est un exercice de la deuxième année du collège. Voici la solution: On a CAH+HAB=90°. (angles) Donc 2EAH+2HAD=2*45°. (angles) Donc EAH+HAD=45°. (angles) Donc EAD=45°. (angle) Donc EAD+DAB=45°+DAB. (angles) Donc EAB=45°+DAB. (angles) ==>(1) D'autre part, on a BEA est un angle extérieur au triangle EAC. Donc BEA=ECA+EAC. (angles) Donc BEA=90°-CAH+EAC. (angles) Donc BEA=45°+45°-(CAE+EAH)+EAC. (angles) Donc BEA=45°+EAH+HAD-CAE-EAH+EAC. (angles) Donc BEA=45°+HAD. (angles) ==>(2) On a AD est bissectrice de l'angle HAB. Donc HAD=DAB. (angles) Donc 45°+HAD=45°+DAB. (angles) Donc, selon 1 et 2, BEA=EAB. (angles) Donc le triangle BEA est isocèle en B. Donc BA=BE. Et par analogie AC=CD. Donc AB+AC=BE+CD. Donc AB+AC=BE+CE+ED. Donc AB+AC=BC+ED. CQFD. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Lun 30 Aoû 2010, 17:44 Lun 30 Aoû 2010, 17:44 | |
| - M.Marjani a écrit:
- nmo a écrit:
Je ne pense pas.
Exemple a=5 et b=1 et c=4.5 .
Du fait a-2b est positif. - Spoiler:
Madich 3lya, rani sayam : )
Inégalité crée par moi: (a,b,c) des réels postives tel que 1=<c=<2, donc démontrez que: (a+b+c)² >= 2c(bc+ac)+4ab =< 4(ab+bc+ac)
Autre déducations:
(a,b,c) les cotés d'un triangle. Démontrer que : a+b+c =< 2V(ab+bc+ac) Il faut que tu reprends ton travail car on ne peut pas passer à a+b+c =< 2V(ab+bc+ac) avec les liens logique que tu as utilisé. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Exo Sujet: Re: Exo  Lun 30 Aoû 2010, 17:57 Lun 30 Aoû 2010, 17:57 | |
| - nmo a écrit:
Il faut que tu reprends ton travail car on ne peut pas passer à a+b+c =< 2V(ab+bc+ac) avec les liens logique que tu as utilisé. Pourquoi? a²+b²+c²=<2(ab+bc+ca) <=> (a+b+c)²=<4(ab+bc+ca) <=> a+b+c=<2V(ab+bc+ac) | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Ven 03 Sep 2010, 13:06 Ven 03 Sep 2010, 13:06 | |
| - M.Marjani a écrit:
- nmo a écrit:
Il faut que tu reprends ton travail car on ne peut pas passer à a+b+c =< 2V(ab+bc+ac) avec les liens logique que tu as utilisé.
Pourquoi?
a²+b²+c²=<2(ab+bc+ca) <=> (a+b+c)²=<4(ab+bc+ca) <=> a+b+c=<2V(ab+bc+ac) Certes. Mais moi, je parle de (a+b+c)² >= 2c(bc+ac)+4ab, tu dis que c'est valable pour tout c compris entre 1 et 2 et a et b deux réels positifs. Je te dis, prends a=b=c=2, l'inégalité n'est pas vérifié. En plus de ça, tu écris (a+b+c)² >= 2c(bc+ac)+4ab =< 4(ab+bc+ac). Ce qui n'est pas bien logique et mathématique. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Exo Sujet: Re: Exo  Ven 03 Sep 2010, 17:04 Ven 03 Sep 2010, 17:04 | |
| - nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
Il faut que tu reprends ton travail car on ne peut pas passer à a+b+c =< 2V(ab+bc+ac) avec les liens logique que tu as utilisé.
Pourquoi?
a²+b²+c²=<2(ab+bc+ca) <=> (a+b+c)²=<4(ab+bc+ca) <=> a+b+c=<2V(ab+bc+ac) Certes.
Mais moi, je parle de (a+b+c)² >= 2c(bc+ac)+4ab, tu dis que c'est valable pour tout c compris entre 1 et 2 et a et b deux réels positifs.
Je te dis, prends a=b=c=2, l'inégalité n'est pas vérifié.
En plus de ça, tu écris (a+b+c)² >= 2c(bc+ac)+4ab =< 4(ab+bc+ac).
Ce qui n'est pas bien logique et mathématique. Il faut réviser: 1=<c= <2 (a+b+c)² >= 2c(bc+ac)+4ab
4(ab+bc+ac) >= 2c(bc+ac)+4ab | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Mar 07 Sep 2010, 12:07 Mar 07 Sep 2010, 12:07 | |
| - M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
Il faut que tu reprends ton travail car on ne peut pas passer à a+b+c =< 2V(ab+bc+ac) avec les liens logique que tu as utilisé. Pourquoi?
a²+b²+c²=<2(ab+bc+ca) <=> (a+b+c)²=<4(ab+bc+ca) <=> a+b+c=<2V(ab+bc+ac) Certes.
Mais moi, je parle de (a+b+c)² >= 2c(bc+ac)+4ab, tu dis que c'est valable pour tout c compris entre 1 et 2 et a et b deux réels positifs.
Je te dis, prends a=b=c=2, l'inégalité n'est pas vérifié.
En plus de ça, tu écris (a+b+c)² >= 2c(bc+ac)+4ab =< 4(ab+bc+ac).
Ce qui n'est pas bien logique et mathématique. Il faut réviser: 1=<c=<2
(a+b+c)² >= 2c(bc+ac)+4ab
4(ab+bc+ac) >= 2c(bc+ac)+4ab Appelons (a+b+c)² >= 2c(bc+ac)+4ab la condition 1 et 4(ab+bc+ac) >= 2c(bc+ac)+4ab la condition 2. Tu ne peux pas passer de 2 à 1, et c'est la faute que tu as commis. Or, tu me dis que 1=<c=<2, mais en particulier, a=b=c=2 ne vérifie pas l'inégalité. Laisse tomber. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Exo Sujet: Re: Exo  Mer 08 Sep 2010, 14:11 Mer 08 Sep 2010, 14:11 | |
| - nmo a écrit:
Appelons (a+b+c)² >= 2c(bc+ac)+4ab la condition 1 et 4(ab+bc+ac) >= 2c(bc+ac)+4ab la condition 2.
Tu ne peux pas passer de 2 à 1, et c'est la faute que tu as commis.
Or, tu me dis que 1=<c=<2, mais en particulier, a=b=c=2 ne vérifie pas l'inégalité.
Laisse tomber. Je veux dire il faut vérifier 1=<c <2 Elle prouvable par une methode de collége. Je ne sais pas s'il y avait une error lors du frappe. - Citation :
- (a+b+c)² >= 2c(bc+ac)+4ab
4(ab+bc+ac) >= 2c(bc+ac)+4ab Ce n'est pas important qu'il aurait une implication entre les deux phrases.. Sinon l'exo reste joli sauf error ! | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Mer 08 Sep 2010, 15:11 Mer 08 Sep 2010, 15:11 | |
| - Dijkschneier a écrit:
- Il semblerait qu'il n'y ait pas de collégiens par ici, nmo.
Suite à ta remarque, je propose un dernier exercice: Soient A, B et C des réels tels que: ^{-1}+\big(\sqrt{6}-\sqrt{5})^{-1}) . 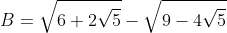 . 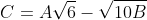 . Démontrez que C est un entier. Bonne chance.P.S: je ne suis pas trop certain de l'exercice de M.Marjani, car en un premier temps, l'inégalité n'était pas vérifiée pour a=b=c=2. Lorsque je refais le calcul ce jour, elle est vérifiée pour a=b=c=2!!! C'est bon en tout cas. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Jeu 09 Sep 2010, 13:15 Jeu 09 Sep 2010, 13:15 | |
| - M.Marjani a écrit:
- nmo a écrit:
Appelons (a+b+c)² >= 2c(bc+ac)+4ab la condition 1 et 4(ab+bc+ac) >= 2c(bc+ac)+4ab la condition 2.
Tu ne peux pas passer de 2 à 1, et c'est la faute que tu as commis.
Or, tu me dis que 1=<c=<2, mais en particulier, a=b=c=2 ne vérifie pas l'inégalité.
Laisse tomber. Je veux dire il faut vérifier 1=<c<2 Elle prouvable par une methode de collége.
Je ne sais pas s'il y avait une error lors du frappe.
- Citation :
- (a+b+c)² >= 2c(bc+ac)+4ab
4(ab+bc+ac) >= 2c(bc+ac)+4ab Ce n'est pas important qu'il aurait une implication entre les deux phrases..
Sinon l'exo reste joli sauf error ! Tu m'as eu hier, cher M.Marjani. J'explique ce que je veux dire dès le début: Je parle de: (a+b+c)²>=2c(bc+ac)+4ab. Qui équivaut à a²+b²+c²+2ab+2bc+2ca>=2c²(a+b)+4ab. Donc a²+b²+c²+2c(a+b)>=2c²(a+b)+2ab. Et puisque a²+b²>=2ab. Il suffit de démontrer que c²+2c(a+b)>=2c²(a+b). C'est à dire que c+2(a+b)>=2c(a+b). Cette écriture n'est pas valables pour certaines valeurs de c de l'intervalle [1,2], et voici pourquoi: Tu supposes que a et b décrivent IR. Par exemple, considérons a=b=c. Alors c+2(c+c)>=2c(c+c). Donc c+2*2c>=2c*2c. Donc c+4c>=4c². Donc 5c>=4c². Donc 5>=4c. Donc 5/4>=c. Alors, tu dois changer les condition de l'exercice. | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Exo Sujet: Re: Exo  | |
| |
|   | | | | Exo |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
