M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Exo Sujet: Re: Exo  Jeu 09 Sep 2010, 14:10 Jeu 09 Sep 2010, 14:10 | |
| - nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
Appelons (a+b+c)² >= 2c(bc+ac)+4ab la condition 1 et 4(ab+bc+ac) >= 2c(bc+ac)+4ab la condition 2.
Tu ne peux pas passer de 2 à 1, et c'est la faute que tu as commis.
Or, tu me dis que 1=<c=<2, mais en particulier, a=b=c=2 ne vérifie pas l'inégalité.
Laisse tomber. Je veux dire il faut vérifier 1=<c<2 Elle prouvable par une methode de collége.
Je ne sais pas s'il y avait une error lors du frappe.
- Citation :
- (a+b+c)² >= 2c(bc+ac)+4ab
4(ab+bc+ac) >= 2c(bc+ac)+4ab Ce n'est pas important qu'il aurait une implication entre les deux phrases..
Sinon l'exo reste joli sauf error ! Tu m'as eu hier, cher M.Marjani.
J'explique ce que je veux dire dès le début:
Je parle de: (a+b+c)²>=2c(bc+ac)+4ab.
Qui équivaut à a²+b²+c²+2ab+2bc+2ca>=2c²(a+b)+4ab.
Donc a²+b²+c²+2c(a+b)>=2c²(a+b)+2ab.
Et puisque a²+b²>=2ab.
Il suffit de démontrer que c²+2c(a+b)>=2c²(a+b).
C'est à dire que c+2(a+b)>=2c(a+b).
Cette écriture n'est pas valables pour certaines valeurs de c de l'intervalle [1,2], et voici pourquoi:
Tu supposes que a et b décrivent IR.
Par exemple, considérons a=b=c.
Alors c+2(c+c)>=2c(c+c).
Donc c+2*2c>=2c*2c.
Donc c+4c>=4c².
Donc 5c>=4c².
Donc 5>=4c.
Donc 5/4>=c.Alors, tu dois changer les condition de l'exercice. Je prends en considérance les ambiances du Ramadan (les errors sont supposés). Pardonez-moi de dire que à toute fois vous utilisez IAG, ça peut ne pas marcher malheureusement, à cause qu'elle n'est pas si fort de prouver une inégalité jusqu'à son minumum.. Cher nmo, quand t'as utiliser IAG, On ne sait jamais que si sont les premiéres conditions de l'inégalité sont vérifiés ou non. Ca veut dire aprés l'utiliser et donner un contre exemple, on considére ce dernier faux. Enfaite, tous on fais des erreurs, mais c'est pour notre bien qu'ils seront utiles pour nous ! @ bientot | |
|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Mar 14 Sep 2010, 16:26 Mar 14 Sep 2010, 16:26 | |
| - nmo a écrit:
- J'ajoute cet exercice:
x, y, et z sont des réels vérifiant 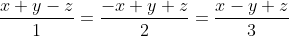 . .
Calculez 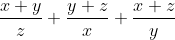 . .
Bonne chance. La réponse est inévitable, la-voici: On a  . Donc  . Donc  . De même  . Et  . On déduit que  . Soit  . Donc  ,  , et  . Et  ,  , et  . On pose  . Donc  . Donc  . Donc  . Donc  . Donc  . Donc  . Sauf erreur. | |
|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exo Sujet: Re: Exo  Mar 14 Sep 2010, 16:51 Mar 14 Sep 2010, 16:51 | |
| - nmo a écrit:
- Dijkschneier a écrit:
- Il semblerait qu'il n'y ait pas de collégiens par ici, nmo.
Suite à ta remarque, je propose un dernier exercice:
Soient A, B et C des réels tels que:
^{-1}+\big(\sqrt{6}+\sqrt{5})^{-1}) . .
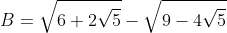 . .
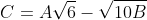 . .
Démontrez que C est un entier.
Bonne chance. Je vais répondre: On a ^{-1}+\big(\sqrt{6}+\sqrt{5})^{-1}) . Donc  . Donc }{(\sqrt{6}+\sqrt{5})(\sqrt{6}-\sqrt{5})}+\frac{1(\sqrt{6}-\sqrt{5})}{(\sqrt{6}+\sqrt{5})(\sqrt{6}-\sqrt{5})}) . Donc }{(\sqrt{6})^2-(\sqrt{5})^2}+\frac{\sqrt{6}-\sqrt{5}}{(\sqrt{6})^2-(\sqrt{5})^2}) . Donc  . Donc  . Donc  . Donc  . Et on a 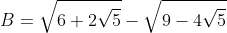 . Donc  . Donc ^2+2\sqrt{5}+1^2}-\sqrt{(\sqrt{5})^2-4\sqrt{5}+2^2}) . Donc ^2}-\sqrt{(\sqrt{5}-2)^2}) . Donc ) . Donc  . Donc  . Et on a 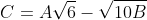 . Donc \sqrt{6}-\sqrt{10*3}) . Donc  . Donc  . Donc 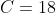 . Ce qui prouve que C est un entier naturel. P.S: J'annonce la clôture de ce jeu. Mais avant, je remercie tout les participants. | |
|
leonidas
Débutant
 Nombre de messages : 2 Nombre de messages : 2
Age : 27
Date d'inscription : 02/01/2011
 |  Sujet: Re: Exo Sujet: Re: Exo  Dim 02 Jan 2011, 13:50 Dim 02 Jan 2011, 13:50 | |
| nn stp je veut encore des exo je suis collegien svp  | |
|
leonidas
Débutant
 Nombre de messages : 2 Nombre de messages : 2
Age : 27
Date d'inscription : 02/01/2011
 |  Sujet: Re: Exo Sujet: Re: Exo  Dim 02 Jan 2011, 13:52 Dim 02 Jan 2011, 13:52 | |
| je suis en 3 année collège | |
|
