| | Un petit défi de géométrie ! |  |
|
|
| Auteur | Message |
|---|
tarask
Expert sup
 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
| | Sujet: Un petit défi de géométrie ! Dim 15 Aoû 2010, 01:14 | |
| Bonsoir tout le monde  je vous propose ce joli exercice de géométrie (j'ai pas eu le temps de le traduir )  Et bonne chance ! | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Un petit défi de géométrie ! Dim 15 Aoû 2010, 13:03 | |
| Merci. Figure : 
Dernière édition par Dijkschneier le Dim 15 Aoû 2010, 13:24, édité 1 fois | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Un petit défi de géométrie ! Dim 15 Aoû 2010, 13:22 | |
| Application directe du théorème de Ceva sous forme trigonométrique, me semble-t-il ? Solution :Les céviennes (AS), (BD) et (EC) sont concourantes. Selon le théorème de Ceva sous forme trigonométrique :  La plupart de ces angles sont connues. En posant x=BAS, et en remarquant que SAC=40-BAS = 40 - x, on obtient une équation de la forme sin(x)/(sin(40-x)) = c, qui est résoluble. On obtient donc x. Il suffit alors de vérifier que x+60 = 90, pour qu'alors le triangle ASB soit rectangle en S. Pour Sylphaen, les droites sont concourantes d'après les données.
Dernière édition par Dijkschneier le Dim 15 Aoû 2010, 13:44, édité 1 fois | |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Un petit défi de géométrie ! Dim 15 Aoû 2010, 13:36 | |
| Oui c'est ça , il suffit de prouver que les droites (AH) et (CE) et (BD) sont concourantes avec H le projeté orthogonale de A sur (BC) . Ce qui est vrai puisqu'on a : 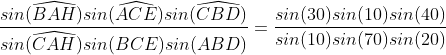 Et :  | |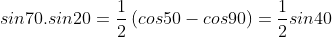
|
| | |
tarask
Expert sup
Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
| | Sujet: Re: Un petit défi de géométrie ! Dim 15 Aoû 2010, 14:47 | |
| oui , bravo le théorème de Ceva était l'idée principale de l'exercice . P.S: jolie figure Dijkschneier  | |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Un petit défi de géométrie ! Dim 15 Aoû 2010, 15:03 | |
| - Dijkschneier a écrit:
- Application directe du théorème de Ceva sous forme trigonométrique, me semble-t-il ?.
Pour Sylphaen, les droites sont concourantes d'après les données. Oui mais pour toi ils sont concourantes parce que t'a pris S comme l'intersection de (AF) et (BC) . Par contre moi j'ai pris H comme étant le projeté orthogonale de A sur (BC) . Et pour prouver que (AF) est perpendiculaire sur (BC) Il suffit de prouver que F £ (AH) c à d les trois droite sont concourantes .. | |
|
| | |
tarask
Expert sup
Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
| | Sujet: Re: Un petit défi de géométrie ! Dim 15 Aoû 2010, 15:15 | |
| re vous pouvez même construire l'équilatéral ABM avec C sur [BM] et travailler avec les triangles isométriques .... pardonnez-moi si je peux pas écrire la solution complète mais la chaleur me gêne vraiment  | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Un petit défi de géométrie ! Dim 15 Aoû 2010, 16:09 | |
| - Sylphaen a écrit:
- Oui mais pour toi ils sont concourantes parce que t'a pris S comme l'intersection de (AF) et (BC) . Par contre moi j'ai pris H comme étant le projeté orthogonale de A sur (BC) . Et pour prouver que (AF) est perpendiculaire sur (BC) Il suffit de prouver que F £ (AH) c à d les trois droite sont concourantes ..
Certes, certes. | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Un petit défi de géométrie ! | |
| |
|
| | |
| | Un petit défi de géométrie ! | |
|
