Défi de géométrie

Soit ABC un triangle, et soient I, J et K les milieux respectifs de AB, BC et AC.

Considérons L, M et N les projections orthogonales de A, B et C sur BC, AC et AB.

Montrer que L, M et N appartiennent au cercle circonscrit au triangle IJK.

Je vous propose cette solution :
[img]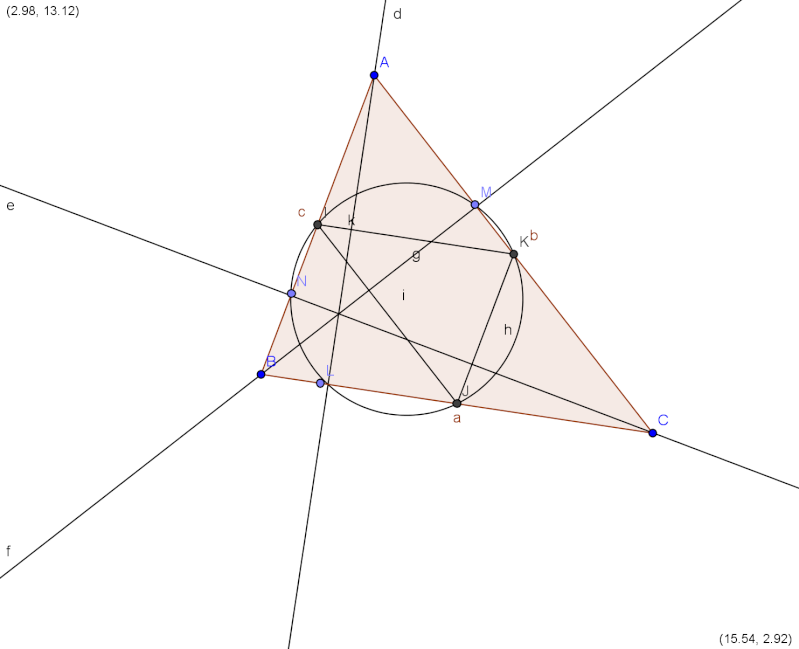[/img]
Il est facile de remarquer que les points , L,N,A,C sont coycliques ( <ANC=<ALC)
donc

<LNC = <LAC
on a maintenant K est milieu de AC et I est milieu de AB
donc IKCJ est un parralélogramme donc :
<JIK=<JCK
De la meme maniere IKJB est un parralélogramme :
donc <JIK=<IJL
on a maintenant <IJL+<INL=<JIK+90+<LNC
=<KCJ+90+<LAC
or on a ALC est un triangle rectangle en L donc <IJL+<INL = 180 , on déduit maintenant que I et N et L et J sont des points cocycliques , vu la symétrie on démontre de la meme maniere que K ,B , M , L sont cycyliques et que N,L,I,K sont cocycliques d'ou le résultat .