Defi de géométrie:

L'exercice est ainsi:
Soit ABC un triangle tel que AB=4, AC=6, et BC=5.
E et D sont deux point tel que D appartient à [AB) et E appartient à [AC).
De telle sorte que AD=3 et AE=2.
Montrez que le quadrilatère ECBD est inscriptible.
Bonne chance.

On : ECBD inscriptible <=> DC.BE=BD.EC+ED.BC

La façons la plus facile c'est de calculer les cosinus des angles de ABC puis trouver DE et BE et DC .

Le résultat en découle ..

Bonjour;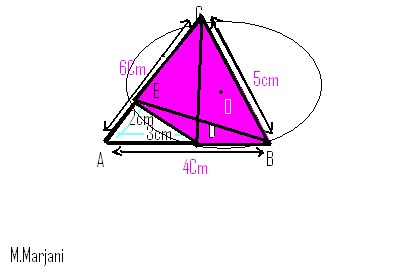



Sans démontrer (une autre fois) le théoréme de potlémée [avec les triangles semblables et Tanassob..]:
Un quadrilatère convexe est inscriptible, si et seulement si la somme des produits des côtés opposés est égale au produit des diagonales.
=> EC × BD + BC × ED = EB × CD.
On va voir donc si cette théoréme satisfait les donées.
-------------------------------------------------------------------------
Calculer [CD] et [BE] en s'aidant du triangle initial avec les triangles semblables pour trouver Cos ou Sin..
-------------------------------------------------------------------------
Ou bien ce quadrilatère est inscriptible dans un cercle si et seulement si : frac{x}{y}=frac{ad + bc}{ab + cd}

Bonne chance.

salam

El Kashi dans ABC =====> cosA=9/16

ElKashi dans ADE =====> DE= 5/2=2,5

comparons les deux triangles :

AB=4 -----------------> 2.AE
AC=6 -----------------> 2.AD
BC=5 -----------------> 2.DE

ils sont semblables

les angles associés

A --------> A
B --------> E
C --------> D
------------------------
Dans ECBD : Deux angles opposés sont supplémentaires

====> il est inscriptible.

.

svp vous pouver m'expliquer "inscriptible"
dans le maths

salam

ABCD est inscriptible( sous entendu dans un cercle)

signifie

A,B,C et D appartiennent à un même cercle.

.--------------------------------

houssa a écrit:

salam

El Kashi dans ABC =====> cosA=9/16

ElKashi dans ADE =====> DE= 5/2=2,5
comparons les deux triangles :

AB=4 -----------------> 2.AE
AC=6 -----------------> 2.AD
BC=5 -----------------> 2.DE

ils sont semblables

les angles associés

A --------> A
B --------> E
C --------> D
------------------------
Dans ECBD : Deux angles opposés sont supplémentaires

====> il est inscriptible.

.

Sans faire ce qui est en rouge, et en t'aidant seulement du deuxième cas de ressemblance, tu trouves que les deux triangles sont semblables.
On est encore en troisième année du collège, et on ne connait ni potlémée, ni Alkashi.
Quand même, Bravo.

houssa a écrit:

salam

ABCD est inscriptible( sous entendu dans un cercle)

signifie

A,B,C et D appartiennent à un même cercle.

.--------------------------------

merci