| | Aires égales |  |
|
|
| Auteur | Message |
|---|
houssa
Expert sup
 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
| | Sujet: Aires égales Ven 20 Aoû 2010, 01:02 | |
| exo :
ABCD : un quadrilatère
E un point du plan tel que ABDE soit un parallèlogramme.
Montrer que : ABCD et ACE ont la même aire.
............... | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: A Ven 20 Aoû 2010, 13:20 | |
| Cela est vrai si et seulement si ABCD est un trapèze de bases [AB] et [DC].
Supposons que c'est le cas.
Solution :
Résultats préliminaires :
ABDE est un parallélogramme, donc (AB) || (ED)
ABCD est un trapèze de bases [AB] et [DC], donc (AB) || (DC), et par conséquent, (EC) || (AB).
ABDE est un parallélogramme, donc (AE) || (BD).
Solution du problème :
La notation [.] désigne l'aire.
[ACE] = [AED] + [ACD] (découpage de l'aire en morceaux)
= [AEB] + [ACD] (les triangles AED et AEB sont de même aire car de même base et (AE) || (BD))
= [ABD] + [ACD] (les triangles AEB et ABD sont de même aire car de même base et (AB) || (ED))
[ABCD] = [ABC] + [ACD]
On doit donc montrer que [ABC] = [ABD], ce qui n'est le cas que si (EC) // (AB), et qui est le cas d'après notre supposition. | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Aires égales Ven 20 Aoû 2010, 13:42 | |
| @Dijkshneier: Une cline d'oeil, je n'ai pas lu la methode. Que direz vous de cette figure? :  Donc ABCD n'est pas nécesairement un trapéze ! Pour moi: - Spoiler:
Je vois plutot que EABDC est un pyramide dont la base est un parallélograme ! AEC et BDC deux faces dans le pyramide, [ABD] est le de demi de la surfaçe du parallélograme !  Si l'exercise est juste, on vas déduire une belle theoréme: Si EABDC est un pyramide dont la base est un parrallélograme, donc la somme de [ABD] et [BDC] est égale à [EAC]: [EAC]=[EABD]÷2 + [BDC] D'une autre façon: [ABC]=[EDC]+[EAD] A vous de jouer !
| |
|
| | |
houssa
Expert sup
Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
| | Sujet: Re: Aires égales Ven 20 Aoû 2010, 22:48 | |
| salam
attention:
E est un point du même plan
ecarter donc l'idée de pyramide
la solution : le facile masqué.
.................................... | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Aires égales Sam 21 Aoû 2010, 02:16 | |
| - houssa a écrit:
- la solution : le facile masqué.
Qu'est-ce que cela veut dire ? Avez-vous lu mon observation ? | |
|
| | |
houssa
Expert sup
Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
| | Sujet: Re: Aires égales Sam 21 Aoû 2010, 09:42 | |
| salam
Dijkschneir
ABCD trapèze est un cas particulier
tu as écris :
on doit montrer que [ABC]=[ABD]...................................(EC) // (AB).....
-------------------------
Mais c'est vrai d'apres ta supposition : ABCD trapèze
Le découpage au départ n'est pas vrai dans le cas général.
ce que j'entend par " facile masqué" la traduction de " السهل الممتنع "
.......................... | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Aires égales Sam 21 Aoû 2010, 14:04 | |
| - houssa a écrit:
- salam
Dijkschneir
ABCD trapèze est un cas particulier
tu as écris :
on doit montrer que [ABC]=[ABD]...................................(EC) // (AB).....
-------------------------
Mais c'est vrai d'apres ta supposition : ABCD trapèze
Le découpage au départ n'est pas vrai dans le cas général.
ce que j'entend par " facile masqué" la traduction de " السهل الممتنع "
.......................... Oups... C'est vrai... | |
|
| | |
houssa
Expert sup
Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
| | Sujet: Re: Aires égales Dim 22 Aoû 2010, 11:53 | |
|
j'attend la réponse ?!
......... | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Aires égales Dim 22 Aoû 2010, 12:50 | |
| - houssa a écrit:
-
j'attend la réponse ?!
......... J'ai la réponse, mais je n'ai pas le temps. Je répondrai plus tard. | |
|
| | |
houssa
Expert sup
Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
| | Sujet: Re: Aires égales Lun 23 Aoû 2010, 01:31 | |
| salam
le texte tel qu'il est tiré du livre :
GEOMETRIE - LEBOSSE -HEMERY- CLASSE 1ere A'CMM' - 1962
exercice 153 page 52
--------------------
je pense qu' il faut mentionner : ABCD quadrilatère NON CROISE
---------------------------------------------
| |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Aires égales Mer 25 Aoû 2010, 21:55 | |
| Reportons le plan au repère ) . On a clairement ) , ) , et ) . Et puisque ABDE un paralléllogramme, il vient que 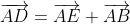 . Donc ) . Posons ) . On a ) , pour chaque couple de points M et N. Donc, on aboutit à ) . Et à ) . Et à ) . Et à ) . Et à ) . On vérifie aussi que =-a) . Et que =-1) . Et que =a-1) . On a =\frac{1}{2}\bigg|\det(\overrightarrow{CA},\overrightarrow{CE})\bigg|) . Donc =\frac{1}{2}|-a|) . Donc =\frac{1}{2}a) .==>(1) Et on a =S(BAD)+S(BDC)) . Donc =\frac{1}{2}\bigg|\det(\overrightarrow{BA},\overrightarrow{BD})\bigg|+\frac{1}{2}\bigg|\det(\overrightarrow{BD},\overrightarrow{BC})\bigg|) . Donc  . Donc =\frac{1}{2}*1+\frac{1}{2}*(a-1)) . Car, - houssa a écrit:
- ABCD quadrilatère NON CROISE
(Et il vient que a est supérieur à 1). Donc =\frac{1}{2}*(1+a-1)) . Donc =\frac{1}{2}a) .==>(2) De 1 et 2, on tire le résultat voulu. Sauf erreur. | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Aires égales | |
| |
|
| | |
| | Aires égales | |
|
