|
| | Systèmes |  |
| | | Auteur | Message |
|---|
achraf_djy
Expert grade1

 Nombre de messages : 401 Nombre de messages : 401
Age : 33
Localisation : Rabat
Date d'inscription : 01/08/2009
 |  Sujet: Systèmes Sujet: Systèmes  Dim 29 Aoû 2010, 11:39 Dim 29 Aoû 2010, 11:39 | |
| BJR!
Résoudre dans IR² les systèmes:
1-
y²=x^3 -3x²+2x
x²=y3-3y²+2y
2-
2x+xy=1+3v2
x²-2x+y²+2y=4 | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Systèmes Sujet: Re: Systèmes  Dim 29 Aoû 2010, 15:36 Dim 29 Aoû 2010, 15:36 | |
| Bonjour Achraf Cava? Ghbarti ^^ :p
Probléme 1:
On remarque que 1 et 2 deux raçines évidente des deux equations, donc le systéme seras équivalent à:
y²=x(x-1)(x-2)>=0
{
x²=y(y-1)(y-2)>=0
* (0,0) Solution evidente au systéme. Et Si x=<0 donc x(x-1)(x-2)=<0 ==> Absurde.
* On déduit que x>=0 de méme y>=0. Puisque y²/x=(x-1)²-(x-1)>=0 et donc: x>=1, de méme y>=1.
* Si nous faisions la somme de x² et y² on aura vitement aprés simplification:
2(x+y)+xy-2=(x+y)²>=16 ce qui implique: (x+y-1)²=xy-1. Delta affirme que x+y=1
Ce résultat qui est absurde, Ou bien x=y.
* Alors x²=x(x-1)(x-2) => x=0 ou x=(x-1)(x-2) <=> x²-4x+2=0 ,
* x1 = 2-V2 ; x2=2+V2
S={(0,0) ; (2-V2,2-V2) ; (2+V2,2+V2)}
Probléme 2:
Methode1:
Le systéme du départ est équivalent à:
(x-1)²+(y+1)²=6
{
x(y+2)=1+3V2
La premiére équation est d'une cercle qui a pour rayon V6. Et reportant le plan à un repert orthonormé, donc on aura 4 solutions au maximum.
On peut déduire du deuxiéme équation que y=(-2x +3V2 +1)÷x et remplaçant ce résultat dans la premiére equation:
(x-1)²+((-2x +3V2 +1)÷x +1)²=6 <=> x^4-2x^3+2x^2-6V2x-2x+6V2+19-6x²=0
Qui a au moin deux solutions !
Methode 2:
Consiste à remarquer que la deuxiéme équation du dernier systéme est un " هذلول" qu'on peut déduire ses solutions qui couppent (Ox) et (Oy).
Dernière édition par M.Marjani le Ven 03 Sep 2010, 17:29, édité 2 fois | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Systèmes Sujet: Re: Systèmes  Lun 30 Aoû 2010, 15:48 Lun 30 Aoû 2010, 15:48 | |
| - achraf_djy a écrit:
- BJR!
Résoudre dans IR² les systèmes:
1-
y²=x^3 -3x²+2x
x²=y3-3y²+2y
On a \begin{cases}y^2=x^3-3x^2+2x\\x^2=y^3-3y^2+2y\end{cases}) . Par différence des lignes, on obtient ) . Donc  . Donc  . Donc (x^2+xy+y^2)-2(x^2-y^2)+2(x-y)=0) . Donc (x^2+xy+y^2)-(x-y)(2x+2y)+2(x-y)=0) . Donc (x^2+xy+y^2-2x-2y+2)=0) . Donc 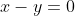 ou  . Donc 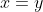 ou  . Donc 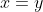 ou  . Donc 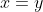 ou ^2+(2-x)^2+(2-y)^2-4=0) . Considérons l'expression A, tel que ^2+(2-x)^2+(2-y)^2-4=0) . Selon Caushy schwartz, \ge(a+b+c)^2) . En posons a=x+y, b=2-x, et c=2-y. On trouve que ^2+(2-x)^2+(2-y)^2\big)\ge(x+y+2-x+2-y)^2) . Donc ^2+(2-x)^2+(2-y)^2\big)\ge 4^2) . Donc ^2+(2-x)^2+(2-y)^2\big)\ge 16) . Donc ^2+(2-x)^2+(2-y)^2\ge \frac{16}{3}) . Donc ^2+(2-x)^2+(2-y)^2-4\ge \frac{16}{3}-4) . Donc  . Donc A ne s'annule point sur IR. Donc 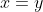 est le cas qu'on considère. Revenons à la première ligne du système, on a  . Donc  . Donc  . Donc =0) . Donc 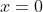 ou  . Considérons le trînome  . Qui a pour discriminent ^2-4*2) . Donc  . Donc  . Ainsi, l'équation  admet deux solutions:  et  . Donc -\sqrt{8}}{2*1}) et +\sqrt{8}}{2*1}) . Donc  et  . Donc  et  . On déduit que les solutions de l'équation  sont  , 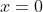 , et  . Donc les solutions du système proposé sont ,(2-\sqrt{2},2-\sqrt{2}),(2+\sqrt{2},2+\sqrt{2})\}) . Sauf erreur. P.S: la solution de M.Marjani est pâle-mêle exposé, même son résultat final est faux.
Dernière édition par nmo le Lun 30 Aoû 2010, 17:52, édité 1 fois | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Systèmes Sujet: Re: Systèmes  Lun 30 Aoû 2010, 17:14 Lun 30 Aoû 2010, 17:14 | |
| - achraf_djy a écrit:
- BJR!
Résoudre dans IR² les systèmes:
2-
2x+xy=1+3v2
x²-2x+y²+2y=4 On a \begin{cases}2x+xy=1+3\sqrt{2}\\x^2-2x+y^2+2y=4\end{cases}) . Donc \begin{cases}2x+xy=1+3\sqrt{2}\\x^2-2x+1+y^2+2y+1=6\end{cases}) . Donc \begin{cases}2x+xy=1+3\sqrt{2}\\(x-1)^2+(y+1)^2=6\end{cases}) . Posons 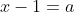 et 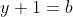 . Alors 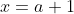 et 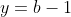 . Donc le système s'écrit \begin{cases}2(a+1)+(a+1)(b-1)=1+3\sqrt{2}\\a^2+b^2=6\end{cases}) .==>(*) Donc \begin{cases}2a+2+ab-a+b-1=1+3\sqrt{2}\\a^2+b^2=6\end{cases}) . Donc \begin{cases}a+ab+b=3\sqrt{2}\\a^2+b^2=6\end{cases}) . Donc \begin{cases}2(a+b)+2ab=6\sqrt{2}\\(a+b)^2-2ab=6\end{cases}) . Et par la somme des lignes, on obtient ^2+2ab-2ab+2(a+b)=6+6\sqrt{2}) . Donc ^2+2(a+b)+1=7+6\sqrt{2}) . Donc ^2=7+6\sqrt{2}) . Donc  ou  . Donc  ou  . Le premier cas:  . Remplaçons dans *, on trouve \begin{cases}2(\sqrt{7+6\sqrt{2}}-b)+(\sqrt{7+6\sqrt{2}}-b)(b-1)=1+3\sqrt{2}\\a^2+b^2=6\end{cases}) . Donc \begin{cases}2\sqrt{7+6\sqrt{2}}-2b+b\sqrt{7+6\sqrt{2}}-\sqrt{7+6\sqrt{2}}-b^2+b=1+3\sqrt{2}\\a^2+b^2=6\end{cases}) . Donc \begin{cases}\sqrt{7+6\sqrt{2}}-b+b\sqrt{7+6\sqrt{2}}-b^2=1+3\sqrt{2}\\a^2+b^2=6\end{cases}) . Donc \begin{cases}\sqrt{7+6\sqrt{2}}-b(1-\sqrt{7+6\sqrt{2}})-b^2=1+3\sqrt{2}\\a^2+b^2=6\end{cases}) . Donc \begin{cases}-\sqrt{7+6\sqrt{2}}-1-3\sqrt{2}+b(1-\sqrt{7+6\sqrt{2}})+b^2=0\\a^2+b^2=6\end{cases}) . La première ligne de ce système est une équation du second degré dont le discriminent est positif. Dans ce cas, on est englué dans un tas de calcul, je renonce: je ne peut pas continuer. Le second cas:  . De même, je renonce. J'attends quelqu'un me confirmer la démarche.
Dernière édition par nmo le Mar 07 Sep 2010, 13:44, édité 1 fois | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Systèmes Sujet: Re: Systèmes  Mar 31 Aoû 2010, 13:15 Mar 31 Aoû 2010, 13:15 | |
| - nmo a écrit:
- P.S: la solution de M.Marjani est pâle-mêle exposé, même son résultat final est faux.
Ah, bon? Je pense que toi aussi t'as oublie le couple (0,0) [EDIT]  Il faut discuter de ce couple avant, non pas l'inclure directement dans les solutions ^^ (x+y-1)²=xy-1 qui est Delta de 2(x+y)+xy-2=(x+y)² est plus fort. C'est juste une faute d'innatention, puisqu'on est dans ramadan, je n'ai pas discuter du cas d'égalité (x=y). Mais la methode reste toujours juste est courte. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Systèmes Sujet: Re: Systèmes  Ven 03 Sep 2010, 11:57 Ven 03 Sep 2010, 11:57 | |
| - M.Marjani a écrit:
- nmo a écrit:
- P.S: la solution de M.Marjani est pâle-mêle exposé, même son résultat final est faux.
Ah, bon?
Je pense que toi aussi t'as oublie le couple (0,0) [EDIT] 
Il faut discuter de ce couple avant, non pas l'inclure directement dans les solutions ^^
(x+y-1)²=xy-1 qui est Delta de 2(x+y)+xy-2=(x+y)² est plus fort. C'est juste une faute d'innatention, puisqu'on est dans ramadan, je n'ai pas discuter du cas d'égalité (x=y). Mais la methode reste toujours juste est courte. Je n'ai rien oublié. Et en plus, je n'ai pas inclus le couple (0,0) dans la solution, mais j'ai prouvé qu'il s'agit d'une solution. Je donne le ballon à un autre membre pour jujer ta solution, M.Marjani. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Systèmes Sujet: Re: Systèmes  Ven 03 Sep 2010, 17:32 Ven 03 Sep 2010, 17:32 | |
| - nmo a écrit:
Je n'ai pas inclus le couple (0,0) dans la solution.
Je donne le ballon à un autre membre pour jujer ta solution, M.Marjani. C'est clair la soluc... Pour le deuxiéme exercise, t'as utilisé la méme demarche que j'ai fais dans les deux EX ^_^ Bon t'as compliqué les choses, tu n'as pas pu sortir c'est pourquoi tu as renoncé. Regarde comment tu peux sortir façilement ^^ Pour le premier cas:On a façilement:  ^2\Leftrightarrow ab=1+3\sqrt{2}-\sqrt{7+6\sqrt{2}}) Tu auras donc un systéme de trois equations:  (y+2+\sqrt{7+6\sqrt{2}})=1+3\sqrt{2}-\sqrt{7+6\sqrt{2}}) Alors Delta... Et avoir les deux solutions. Alors Delta... Et avoir les deux solutions.De méme pour le deuxiéme cas:  | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Systèmes Sujet: Re: Systèmes  Mar 07 Sep 2010, 14:12 Mar 07 Sep 2010, 14:12 | |
| - M.Marjani a écrit:
- nmo a écrit:
Je n'ai pas inclus le couple (0,0) dans la solution.
Je donne le ballon à un autre membre pour jujer ta solution, M.Marjani. C'est clair la soluc...
Pour le deuxiéme exercise, t'as utilisé la méme demarche que j'ai fais dans les deux EX ^_^
Bon t'as compliqué les choses, tu n'as pas pu sortir c'est pourquoi tu as renoncé.
Regarde comment tu peux sortir façilement ^^
Pour le premier cas:
On a façilement: 
^2\Leftrightarrow ab=1+3\sqrt{2}-\sqrt{7+6\sqrt{2}})
Tu auras donc un systéme de trois equations:

(y+2+\sqrt{7+6\sqrt{2}})=1+3\sqrt{2}-\sqrt{7+6\sqrt{2}})
Alors Delta... Et avoir les deux solutions.
De méme pour le deuxiéme cas:
 Sauf quelques fautes de frappe, la methode est bonne. A priori, j'ai prédit qu'on aurait des solutons. Mais après ce qu'a fait M.Marjani, et après le calcul des discriminents des deux cas, on trouve qu'ils sont strictement négatifs. Ainsi, aucune solution n'existe. Sauf erreur. | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Systèmes Sujet: Re: Systèmes  | |
| |
|   | | | | Systèmes |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
