card P(E) ...

Infaisable avant d'avoir des notions sur le dénombrement.

faisable je te dit ! ! Je L'ai Fais Mais J'ai pas le temp D'écrire la démonstration maintenant J'ai Cour L'aprem je Poste La Démo !

Soit E un ensemble fini à n éléments.
Pour A partie de E, considérons son application caractéristique
χA: E→{ 0,1 }x↦{ 1si x∈A , 0sinon .
L'application A↦χA réalise une bijection de P(E) vers { 0,1 }^E.
Il y a 2^n applications de E dans { 0,1 } d'où le résultat.

Démonstration par dénombrement
Pour construire une partie A d'un ensmbre E={ x1,…,xn } avec x1,…,xn deux à deux distintcs :

* on choisit si x1∈A ou non : 2 possibilités ;
* on choisit si x2∈A ou non : 2 possibilités ;
...
* on choisit si xn∈A ou non : 2 possibilités.
Au total, il y a 2^n possibilités de construction et autant parties de E.

Ca me fait rapelle au tableau de vérité !
Quand il s'agit de deux phrases mathématiques (P) et (Q) on aura 2^2 cases horizontales.
Quand ils s'agit de 3, on aura 2^3 Et quand il s'agit d'une seule phrase: 2^1 cases (quand t-elle sera juste et quand t-elle sera fausse)... Et ansi de suite !

On déduit que: P(E)=2^{n}

Notez que:
Le nombre des cases horizontales = P(E)
Le nombre des phrases mathématique: n

(J'ai pas encore fais les applications dans les ensembles c'est pourquoi que j'ai pas arrivé à te donner une solution compléte.)

Les solutions les plus simples sont celles qui ont été donné par amazigh-tisffola. Ne t'attend pas à plus simple.

amazigh-tisffola a écrit:

L'application A↦χA réalise une bijection de P(E) vers { 0,1 }^E.

Je pense qu'il faut mettre l'ensemble des applications au lieu de ce qui est en rouge.
Un autre problème consiste à démontrer la bijection, ce qui n'est pas du niveau.
Je présente une autre solution dans mon prochain message.

Voici une autre solution:
Considérons un ensemble E fini à n élément.
L'ensemble des parties de E se compose des sous ensembles:
-à 0 éléments, leurs nombre est .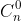
-à 1 un élément, leurs nombre est .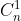
...
-à n élémets, leurs nombre est .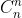
Afin de calculer le nombre de parties de E, on calcule la somme .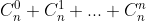
On a selon le binôme de Newton, .
On prends a=b=1, on trouve .
Donc .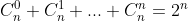
Sauf erreur.

BSR à Vous !!

Celà fait un bout de temps !!! .... Des soucis .... Mais c'est là des choses personnelles !!

Je vois là une Démonstration Par Récurrence assez séduisante et de votre niveau !!
Alors , allons y !!!

Nous allons prouver par récurrence sur n , la propriété suivante :
P(n) : { Si E est un ensemble à n éléments alors P(E) a 2^n éléments }

La Propriété est vraie pour n=0 ( par convention ) : si E=VIDE alors P(E)={VIDE} donc a 2^0=1 élément .

Hypothèse de Récurrence HR :supposons P(n) VRAIE
Alors soit F un ensemble ayant (n+1) éléments ( distincts) et soit a un élément DONNE de F ; on notera alors E=F\{a} le Complémentaire de {a} par rapport à F , E a pour Cardinal n .

Les sous-ensembles H de F sont de DEUX SORTES :
1) Il y a les parties H de F qui contiennent a , elles sont de la forme H={a}uK avec K élément de P(E) et il y en a EXACTEMENT 2^n puisque CardE=n et d'après HR
2) Il y a les parties H de F qui ne contiennent pas a , ce sont les éléments de P(E) et on en trouve EXACTEMENT 2^n

En tout et pour tout , on en aura donc : 2^n + 2^n soit 2.2^n soit 2^(n+1)
et par conséquent P(n+1) est VRAIE !!!

Amicalement .
Lotus_Bleu