| | Des problèmes lors de la résolutions de certains exercices |  |
|
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Des problèmes lors de la résolutions de certains exercices Sujet: Des problèmes lors de la résolutions de certains exercices  Dim 14 Nov 2010, 18:16 Dim 14 Nov 2010, 18:16 | |
| Démontrez que: (\exists!(a,b)\in\mathbb{N}^2)\begin{cases}(6+\sqrt{5})^n=a+b\sqrt{5}\\a^2-5b^2=31^n\end{cases}) . P.S: Songez-vous à une bijection, laquelle? Bonne chance.
Dernière édition par nmo le Ven 28 Jan 2011, 12:34, édité 5 fois (Raison : Double faute, changer le titre, corriger le Latex) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Dim 14 Nov 2010, 18:28 Dim 14 Nov 2010, 18:28 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Dim 14 Nov 2010, 18:35 Dim 14 Nov 2010, 18:35 | |
| - Dijkschneier a écrit:
- Récurrence. Simple.
Pour l'existance, la récurrence est la bonne voie. Il te reste de prouver l'unicité, et c'est en fait le but de mon message. Ensuite, le texte de l'exercice me semble pareil à démontrez q'une application est bijective. De ce point, ma question est: peut-on la trouver? Merci de me répondre. | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Dim 14 Nov 2010, 18:40 Dim 14 Nov 2010, 18:40 | |
| - nmo a écrit:
- Démontrez que pour tout entier n, il existe un couple unique (a,b) d'entiers naturels tel que
^n=a+b\sqrt{5}\\a^2-5b^2=1\end{cases}) . .
P.S: Songez-vous à une bijection, laquelle?
Bonne chance. BSR à Vous Toutes et Tous !! Il y a un problème !!! Je suis d'accord avec Dijkschneier que (6+rac(5))^n = an +bn.rac(5) se fait à l'aide d'une récurrence sur n ou bien par le Binôme de NEWTON .... Mais alors , on pourrait montrer aussi que (6-rac(5))^n=an -bn.rac(5) auquel cas , par multiplication , on obtiendrait :(an)^2 - 5.(bn)^2 = (36 - 5)^n=(31)^n ????!!!!! Il y a donc une erreur dans l'énoncé .... Amicalement. LHASSANE
Dernière édition par Bison_Fûté le Dim 14 Nov 2010, 18:43, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Dim 14 Nov 2010, 18:43 Dim 14 Nov 2010, 18:43 | |
| - Bison_Fûté a écrit:
- nmo a écrit:
- Démontrez que pour tout entier n, il existe un couple unique (a,b) d'entiers naturels tel que
^n=a+b\sqrt{5}\\a^2-5b^2=1\end{cases}) . .
P.S: Songez-vous à une bijection, laquelle?
Bonne chance. BSR à Vous Toutes et Tous !!
Il y a un problème !!!
Je suis d'accord avec Dijkschneier que (6+rac(5))^n = an +bn.rac(5) se fait à l'aide d'une récurrence sur n ou bien par le Binôme de NEWTON ....
Mais alors , on pourrait montrer aussi que (6-rac(5))^n=an -bn.rac(5)
auquel cas , par multiplication , on obtiendrait :(an)^2 - 5.(bn)^2 = 36 - 5=31
Il y a donc une erreur dans l'énoncé ....
Amicalement. LHASSANE Tu as raison, le 3 m'est echappé. C'est rectifié. | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Dim 14 Nov 2010, 18:47 Dim 14 Nov 2010, 18:47 | |
| BSR nmo !!
Il y a encore ERREUR ! C'est (31)^n qu'il faut mettre
Amicalement . LHASSANE | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Dim 14 Nov 2010, 18:47 Dim 14 Nov 2010, 18:47 | |
| - Bison_Fûté a écrit:
- BSR nmo !!
Il y a encore ERREUR ! C'est (31)^n qu'il faut mettre
Amicalement . LHASSANE Tu m'as eu, c'est bien ça. C'est édité. C'est vraiment un problème d'écriture, le n m'a échappé aussi, j'ai vraiment honte. Maintenant, je pense que le problème est bien rédigé. J'attends impatiemment des réponses à ma questions. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Dim 14 Nov 2010, 19:12 Dim 14 Nov 2010, 19:12 | |
| - nmo a écrit:
- Dijkschneier a écrit:
- Récurrence. Simple.
Il te reste de prouver l'unicité, et c'est en fait le but de mon message. Simple aussi. Supposer qu'il existe deux couples (a,b) et (c,d) qui vérifient ce qui est demandé et montrer qu'en vérité (a,b)=(c,d). | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mar 16 Nov 2010, 12:42 Mar 16 Nov 2010, 12:42 | |
| - Dijkschneier a écrit:
- nmo a écrit:
- Dijkschneier a écrit:
- Récurrence. Simple.
Il te reste de prouver l'unicité, et c'est en fait le but de mon message. Simple aussi. Supposer qu'il existe deux couples (a,b) et (c,d) qui vérifient ce qui est demandé et montrer qu'en vérité (a,b)=(c,d). Bon, c'est ça ce qu'il faut faire, on aboutit facilement au résultat. Qu'en peses-tu de ma question? N'as tu pas pensé à une application bijective? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mar 16 Nov 2010, 13:04 Mar 16 Nov 2010, 13:04 | |
| Un nouvel problème: Soit 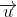 un vecteur non nul, et soit (D) une droite dont le vecteur directeur est 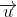 . 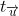 est la translation par le vecteur 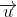 et }) la reflexion d'axe (D). 1-Démontrez que }=S_{(D)}\circ t_{\overrightarrow{u}}) . 2-Démontrez que }) est une application bijective et précisez })^{-1}) . Ma réponse pour le premier: Avec un peu de géométrie plane, le résultat est trouvée. Mais, pensons à la géométrie analytique: Reportons le plan au repère ) tel que I est le projeté d'un point quelquonque M du plan. Notons ) et ) . D'une part, Soit N l'image de M par 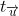 . Facile à trouver que ) . Soit N' l'image de N par }) . Facile aussi à trouver que ) .==>(1) D'autre part, Soit P l'image de M par }) . Facile à trouver que ) . Soit P' l'image de P par 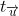 . Facile aussi à trouver que ) .==>(2) De 1 et 2, on trouve que N'#P'. Ce qui contredit ce du'on doit prouver. Où est la faute, merci de me répondre car cela me cause vraiment un problème. Je vous laisse faire le deuxième. Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mer 24 Nov 2010, 17:36 Mer 24 Nov 2010, 17:36 | |
| J'attends impatiemment des réponses, surtout pour le deuxième. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mer 24 Nov 2010, 18:54 Mer 24 Nov 2010, 18:54 | |
|
salam
excuses moi , beaucoup de maladresses
*) repère (I v(IM) , v(U) ) et tu dis M quelconque de P...... çà colle pas !!!
un repère doit être fixé
___________________________________________
par exemple :
soit O un point fixé sur (D) ,
v(u) peut être choisi comme vecteur directeur de (D) supposé en plus comme unité
soit (D') perpendiculaire à (D) en O
soit v(u') un vecteur directeur de (D') unitaire
ALORS : (O , u , u' ) est repère ORTHONORME du plan ( c'est nécéssaire)
________________________________________________
ensuite : soit M un point queconque du plan ===> M(x,y) dans ce repère.
on commence par trouver M'(x',y') = S(D) (M)
====> x' = x et y' = -y
___________________________________
puis on cherche M"(x",y") = Tu (M')
====> v(M'M") =u
=====> x" -x' = 1 et y" -y' = 0
=====> x" = x'+1 et y" = y'
_________________________
maintenant tu passes à : Tu o S(D)
M" = TuoS(D) (M)
=====> x" = x+1 et y" = -y
tu obtiens les expressions analytiques de TuoS(D)
_______________
pour montrer que c'est une bijection
il faut montrer que :
pour tout M" du plan il existe M unique tel que M" = TuoS(D) (M)
donc il faut résoudre le système :
x+1 = x"
-y = y"
_________________________
tu vois c'est simple
x = x"-1
y = - y"
d'où l'existence et l'unicité de M.
==================================
Remarque :
si vous avez etudié les propriétés des translations === > il y a la bijection.
de même pour les symétries axiales .
d'où la composée de deux bijections est une bijection et le problème est résolu.
=====================================
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Sam 27 Nov 2010, 18:26 Sam 27 Nov 2010, 18:26 | |
| - houssa a écrit:
salam
excuses moi , beaucoup de maladresses
*) repère (I v(IM) , v(U) ) et tu dis M quelconque de P...... çà colle pas !!!
un repère doit être fixé
__________________________________________
par exemple :
soit O un point fixé sur (D) ,
v(u) peut être choisi comme vecteur directeur de (D) supposé en plus comme unité
soit (D') perpendiculaire à (D) en O
soit v(u') un vecteur directeur de (D') unitaire
ALORS : (O , u , u' ) est repère ORTHONORME du plan ( c'est nécéssaire)
________________________________________________
ensuite : soit M un point queconque du plan ===> M(x,y) dans ce repère.
on commence par trouver M'(x',y') = S(D) (M)
====> x' = x et y' = -y
___________________________________
puis on cherche M"(x",y") = Tu (M')
====> v(M'M") =u
=====> x" -x' = 1 et y" -y' = 0
=====> x" = x'+1 et y" = y'
_________________________
maintenant tu passes à : Tu o S(D)
M" = TuoS(D) (M)
=====> x" = x+1 et y" = -y
tu obtiens les expressions analytiques de TuoS(D)
_______________
pour montrer que c'est une bijection
il faut montrer que :
pour tout M" du plan il existe M unique tel que M" = TuoS(D) (M)
donc il faut résoudre le système :
x+1 = x"
-y = y"
_________________________
tu vois c'est simple
x = x"-1
y = - y"
d'où l'existence et l'unicité de M.
==================================
Remarque :
si vous avez etudié les propriétés des translations === > il y a la bijection.
de même pour les symétries axiales .
d'où la composée de deux bijections est une bijection et le problème est résolu.
=====================================
Tout cela est bon, je comprends maintenant ma faute. Je ma demande aussi: comment déterminer la bijection réciproque? Merci pour tes réponses. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Sam 27 Nov 2010, 18:35 Sam 27 Nov 2010, 18:35 | |
| Un nouvel problème qui me bloque parfaitement, à cause de la faute dans le livre: Voici l'exercice modifié: Soit ABCD un parallélogramme. Soit N et M deux points tel que ;(A,3)\}) et ;(A,3);(C,3)\}) . On définit aussi R et S avec: 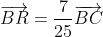 et 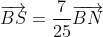 . Trouvez trois entiers (x,y,z), tel que ;(B,y);(C,z)\}) . Ensuite dites si M, R, et S sont rectilignes. Bonne chance.P.S: J'attends impatiemment une réponse. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mer 08 Déc 2010, 17:36 Mer 08 Déc 2010, 17:36 | |
| Pour le problème précédant, je sais maintenant la réponse, à l'aide du calcul analytique. Je vous demande de m'aider à résoudre cet exercice qui va être utile pour moi: Discuter selon les valeurs du paramètre réel m les solutions réelles de l'équation 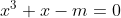 . P.S: géométriquement parlant, on dessine la courbe représentative de la fonction 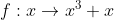 . Puis, on remarque que quelquesoit la valeur de m, la droite :y=m) coupe cette courbe, d'où: l'équation 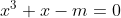 admet des solutions réelles quelque soit m. D'un autre côté, on peut remarquer que l'application 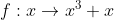 est bijective de IR* vers IR*. Ce qui peut assurer la réponse géométrique. Mais la question, c'est de trouver x en fonction de m. Je serai très reconnaissant à celui qui va résoudre cet exercice. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mer 08 Déc 2010, 17:52 Mer 08 Déc 2010, 17:52 | |
| Bonsoir nmo .
Puisque tu veux "Discuter selon les valeurs du paramètre réel m les solutions réelles de l'équation" j'ai une idée vite faite : ne peut-on pas utiliser la formule de Cardan , et discuter la solution trouvée selon m (appartient à R ou bien à C\R ) ? Je n'ai pas essayé parce que je dois quitter dans un moment . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mer 08 Déc 2010, 17:57 Mer 08 Déc 2010, 17:57 | |
| - tarask a écrit:
- Bonsoir nmo .
Puisque tu veux "Discuter selon les valeurs du paramètre réel m les solutions réelles de l'équation" j'ai une idée vite faite : ne peut-on pas utiliser la formule de Cardan , et discuter la solution trouvée selon m (appartient à R ou bien à C\R ) ? Je n'ai pas essayé parce que je dois quitter dans un moment . C'est là ou réside le problème, je ne maitrise pas bien cette methode. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mer 08 Déc 2010, 18:01 Mer 08 Déc 2010, 18:01 | |
| - nmo a écrit:
- tarask a écrit:
- Bonsoir nmo .
Puisque tu veux "Discuter selon les valeurs du paramètre réel m les solutions réelles de l'équation" j'ai une idée vite faite : ne peut-on pas utiliser la formule de Cardan , et discuter la solution trouvée selon m (appartient à R ou bien à C\R ) ? Je n'ai pas essayé parce que je dois quitter dans un moment . C'est là ou réside le problème, je ne maitrise pas bien cette methode. Pas de panique , voici un joli pdf qui va te permettre de comprendre cette formule http://www.mathforu.com/pdf/equations-troisieme-degre.pdf (formule vers la page 5/7 mais tu dois tout lire pour bien assimiler) Bonne découverte . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mer 08 Déc 2010, 18:04 Mer 08 Déc 2010, 18:04 | |
| - tarask a écrit:
- nmo a écrit:
- tarask a écrit:
- Bonsoir nmo .
Puisque tu veux "Discuter selon les valeurs du paramètre réel m les solutions réelles de l'équation" j'ai une idée vite faite : ne peut-on pas utiliser la formule de Cardan , et discuter la solution trouvée selon m (appartient à R ou bien à C\R ) ? Je n'ai pas essayé parce que je dois quitter dans un moment . C'est là ou réside le problème, je ne maitrise pas bien cette methode. Pas de panique , voici un joli pdf qui va te permettre de comprendre cette formule http://www.mathforu.com/pdf/equations-troisieme-degre.pdf (formule vers la page 5/7 mais tu dois tout lire pour bien assimiler)
Bonne découverte .
Merci infiniment. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mer 08 Déc 2010, 18:06 Mer 08 Déc 2010, 18:06 | |
| - nmo a écrit:
- tarask a écrit:
- nmo a écrit:
- tarask a écrit:
- Bonsoir nmo .
Puisque tu veux "Discuter selon les valeurs du paramètre réel m les solutions réelles de l'équation" j'ai une idée vite faite : ne peut-on pas utiliser la formule de Cardan , et discuter la solution trouvée selon m (appartient à R ou bien à C\R ) ? Je n'ai pas essayé parce que je dois quitter dans un moment . C'est là ou réside le problème, je ne maitrise pas bien cette methode. Pas de panique , voici un joli pdf qui va te permettre de comprendre cette formule http://www.mathforu.com/pdf/equations-troisieme-degre.pdf (formule vers la page 5/7 mais tu dois tout lire pour bien assimiler)
Bonne découverte .
Merci infiniment. Avec plaisir. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Ven 10 Déc 2010, 12:32 Ven 10 Déc 2010, 12:32 | |
| Alors nmo , ça donne un résultat ou pas ? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Ven 10 Déc 2010, 12:42 Ven 10 Déc 2010, 12:42 | |
| - tarask a écrit:
- Alors nmo , ça donne un résultat ou pas ?
Le pdf est utile, mais le calcul serait ample avec la formule donnée. Merci encore une fois. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Ven 10 Déc 2010, 12:57 Ven 10 Déc 2010, 12:57 | |
| - nmo a écrit:
- tarask a écrit:
- Alors nmo , ça donne un résultat ou pas ?
Le pdf est utile, mais le calcul serait ample avec la formule donnée.
Merci encore une fois. Oui , c'est ce que je reproche à cette formule , trop de calcul ! Il y en a d'autres , mais je n'ai pas eu l'occasion de les employer : Méthode de Tschirnhaus: http://fr.wikipedia.org/wiki/M%C3%A9thode_de_Tschirnhaus Méthode de Sotta: http://fr.wikipedia.org/wiki/M%C3%A9thode_de_Sotta Pour le 4ème degré il y a celle de Descartes et Ferrari ... Et de rien  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mer 29 Déc 2010, 15:24 Mer 29 Déc 2010, 15:24 | |
| - tarask a écrit:
- Oui , c'est ce que je reproche à cette formule , trop de calcul !
Il y en a d'autres , mais je n'ai pas eu l'occasion de les employer :
Méthode de Tschirnhaus: http://fr.wikipedia.org/wiki/M%C3%A9thode_de_Tschirnhaus
Méthode de Sotta: http://fr.wikipedia.org/wiki/M%C3%A9thode_de_Sotta
Pour le 4ème degré il y a celle de Descartes et Ferrari ...
Et de rien  Merci, même si cela n'est pas de mon niveau. Je proposerai un nouveau problème de barycentre maintenant. Et j'aime avoir des solutions satisfaisantes. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  Mer 29 Déc 2010, 16:33 Mer 29 Déc 2010, 16:33 | |
| En effet, c'est l'exercice dernier du cette leçon, où on va essayer de démontrer le théorème de ceva à l'aide du barycentre, le voici: Soit ABC un triangle et M un point quelquonque de plan. 1) Les droites (MA), (MB), et (MC) coupent respectivement les droites (BC), (CA), et (AB) en E, F, et G. Soit O un autre point quelquonque du même plan. a-Démontrez l'existance de six rééls x, y, z, a, b, et c de telle sorte que: - 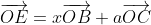 et x+a=1. - 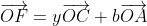 et y+b=1. - 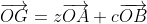 et z+c=1. b-Démontrez l'existance de trois rééls  ,  , et 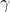 tel que: 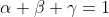 et ,(B;\beta),(C;\gamma)\}) . c-Démontrez que \overrightarrow{OE}=\beta.\overrightarrow{OB}+\gamma.\overrightarrow{OC}) . d-En déduire que 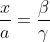 , 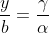 , et 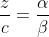 , et puis que xyz=abc. 2) Soit A', B', et C' trois points qui appartiennent respectivement au droites (BC), (CA), et (AB). On pose: 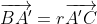 , 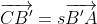 , et 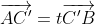 . On suppose que rst=1. Démontrez que les droites (AA'), (BB'), et (CC') sont soit parallèles, soit concourantes en un seul point. Bonne chance.P.S: J'espère recevoir la réponse avant la fin de l'année. Merci d'avance. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Des problèmes lors de la résolutions de certains exercices Sujet: Re: Des problèmes lors de la résolutions de certains exercices  | |
| |
|
  | |
| | Des problèmes lors de la résolutions de certains exercices |  |
|
