| | exercice d'olympiade |  |
|
+2matheux-xman Ahmed Taha (bis) 6 participants |
| Auteur | Message |
|---|
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: exercice d'olympiade Mar 07 Déc 2010, 21:50 | |
| exo 1: a,b et c sont des réels strictement positifs:prouver que :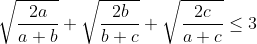 
Dernière édition par abdelkrim-amine le Mar 07 Déc 2010, 22:03, édité 2 fois | |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: exercice d'olympiade Mar 07 Déc 2010, 21:52 | |
| exo 2: n de IN* prouver que: }}{4n+1}%3C&space;\frac{n}{2}) | |
|
| | |
matheux-xman
Féru
Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
| | Sujet: Re: exercice d'olympiade Mar 07 Déc 2010, 22:39 | |
| - abdelkrim-amine a écrit:
- exo 1:
a,b et c sont des réels strictement positifs:prouver que :
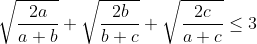Soit : 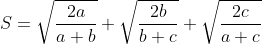 D'aprés l'inégalité de Cauchy-Schwarz : (\frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}})) Qu'on peut écrire d'une autre façon : +(a+c)+(b+c))(\frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}})) si on suppose que : 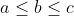 on aura : 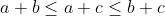 et : 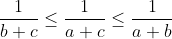 d'aprés l'inégalité de Chebyshev :   | |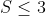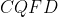
|
| | |
supista
Féru
Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
| | Sujet: Re: exercice d'olympiade Mer 08 Déc 2010, 10:59 | |
| [quote="matheux-xman"] - abdelkrim-amine a écrit:
d'aprés l'inégalité de Chebyshev :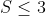
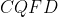c'est faux !!! car l'inégalité de chebyshev donne ((a+b)+(b+c)+(c+a))(1/(a+b)+1(b+c)+1(c+a)) >=9 est pas <= | |
|
| | |
matheux-xman
Féru
Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
| | Sujet: Re: exercice d'olympiade Mer 08 Déc 2010, 14:56 | |
| | |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: exercice d'olympiade Mer 08 Déc 2010, 23:53 | |
| | |
|
| | |
supista
Féru
Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
| | Sujet: Re: exercice d'olympiade Jeu 09 Déc 2010, 11:36 | |
| bjr!!
ton inégalité est difficile voilà le lien de la solution
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=51&t=381520 | |
|
| | |
A446
Maître
Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
| | Sujet: Re: exercice d'olympiade Ven 10 Déc 2010, 14:18 | |
| | |
|
| | |
Hamouda
Maître
Nombre de messages : 125
Age : 30
Date d'inscription : 26/11/2010
| | Sujet: Re: exercice d'olympiade Ven 10 Déc 2010, 15:47 | |
| - abdelkrim-amine a écrit:
- exo 2:
n de IN* prouver que:
es-tu sur que tu n'as pas commis de faute en écrivant ça?^^ | |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: exercice d'olympiade Ven 10 Déc 2010, 18:37 | |
| oui  est ce que vous avez un contre exemple ? | |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: exercice d'olympiade Ven 10 Déc 2010, 18:40 | |
| oui oui ... je suis désolé ... la vrai formule est : }}{4n+1}%3C&space;\frac{n}{2}) | |
|
| | |
matheux-xman
Féru
Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
| | Sujet: Re: exercice d'olympiade Ven 10 Déc 2010, 21:40 | |
| pour le dernier exercice, il faut juste montrer que 2*rac(2n(2n+1))<4n+1 (c'est trés facile) ... puis conclure | |
|
| | |
houssa
Expert sup
Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
| | Sujet: Re: exercice d'olympiade Sam 11 Déc 2010, 07:17 | |
|
salam
1) on montre que Rac(2n.(2n+1)) /(4n+1) < 1/2
on compare les carrés .
2) majorer la somme :
rac(6) / 5 + ....................+rac(2n.(2n+1)) / (4n+1) < n.(1/2)
__________________________________________
| |
|
| | |
Contenu sponsorisé
| | Sujet: Re: exercice d'olympiade | |
| |
|
| | |
| | exercice d'olympiade | |
|
