|
| | Complexe. |  |
| | | Auteur | Message |
|---|
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Complexe. Sujet: Complexe.  Sam 18 Déc 2010, 16:08 Sam 18 Déc 2010, 16:08 | |
| Déterminer les nombres complexes x,y et z de modules inférieurs à 1 et vérifiant xyz=x+y+z=1.
Bonne chance . | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Complexe. Sujet: Re: Complexe.  Sam 18 Déc 2010, 17:50 Sam 18 Déc 2010, 17:50 | |
| Solution :Puisque xyz=1, alors |xyz|=1. Or |x|,|y|,|z| <=1, donc |xyz| <= 1 avec égalité ssi |x|=|y|=|z|=1. On est justement dans le cas d'égalité, donc |x|=|y|=|z|=1. On peut donc écrire : 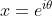 , 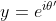 et 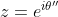 . Par conséquent : 1 = xyz = }) , d'où : ) . Et on a d'autre part : 1 = x+y+z = %20+%20(\sin{\theta}+\sin{\theta%27}+\sin{\theta%27%27})i) , par suite : 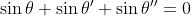 et 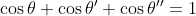 . On en déduit que : }) et }%20=%201) Cela doit bien impliquer que theta et theta' valent en valeur principale soit 0, soit PI/2, soit -PI/2. Synthèse :Les triplets solutions sont (i,-i,1) et toutes les autres permutations.
Dernière édition par Dijkschneier le Lun 20 Déc 2010, 20:51, édité 2 fois | |
|   | | tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Complexe. Sujet: Re: Complexe.  Sam 18 Déc 2010, 18:26 Sam 18 Déc 2010, 18:26 | |
| - Dijkschneier a écrit:
- Solution :
Puisque xyz=1, alors |xyz|=1. Or |x|,|y|,|z| <=1, donc |xyz| <= 1 avec égalité ssi |x|=|y|=|z|=1. On est justement dans le cas d'égalité, donc |x|=|y|=|z|=1.
On peut donc écrire : 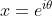 , , 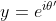 et et 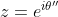 . Par conséquent : 1 = xyz = . Par conséquent : 1 = xyz = }) , d'où : , d'où : ) . .
Et on a d'autre part : 1 = x+y+z = %20+%20(\sin{\theta}+\sin{\theta%27}+\sin{\theta%27%27})i) , par suite : , par suite : 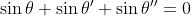
On en déduit que : })
Cela implique que : ) . .
Par suite : x=y=z=1. Bonsoir Dijkschneier ! Très bonne méthode , cependant , il y a quelque chose qui marche pas : dans ton dernier passage : Cela implique que : ) Je ne vois pas d'où vient ça , parce que le moteur Wolfram donne comme solutions à sin(a)+sin(b)=sin(a+b) :  Je serai ravi si tu éclaircis ce passage  | |
|   | | Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Complexe. Sujet: Re: Complexe.  Sam 18 Déc 2010, 18:36 Sam 18 Déc 2010, 18:36 | |
| - Dijkschneier a écrit:
- Solution :
Puisque xyz=1, alors |xyz|=1. Or |x|,|y|,|z| <=1, donc |xyz| <= 1 avec égalité ssi |x|=|y|=|z|=1. On est justement dans le cas d'égalité, donc |x|=|y|=|z|=1.
On peut donc écrire : 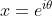 , , 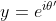 et et 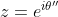 . Par conséquent : 1 = xyz = . Par conséquent : 1 = xyz = }) , d'où : , d'où : ) . .
Et on a d'autre part : 1 = x+y+z = %20+%20(\sin{\theta}+\sin{\theta%27}+\sin{\theta%27%27})i) , par suite : , par suite : 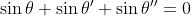 et et 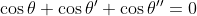 . .
On en déduit que : }) et et }%20=%200)
Cela doit bien impliquer que theta et theta' valent en valeur principale soit 0, soit PI/2, soit -PI/2.
Synthèse :
Les triplets solutions sont (i,-i,1) et toutes les autres permutations. La premiere méthode était fausse la 2eme moins claire parceque cos(teta)+cos(teta')+cos(teta")=1 et non pas 0 et le systeme implqieu que teta valent pi/2 ou -pi/2 et non pas 0 en fait le systeme qu'il faut résoudre c en fait je pose teta=a , teta'=b teta"=c cos(a)+cos(b)+cos(a+b)=1 sin(a)+sin(b)=sin(a+b) ce qui donne apres calculs que : cos(a+b)=cos(pi-a+b) ... et les soltion son bien S={i,-i,1} et les autre permutations cycliques. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Complexe. Sujet: Re: Complexe.  Sam 18 Déc 2010, 18:51 Sam 18 Déc 2010, 18:51 | |
| Oui Sporovitch. Les permutations à la fin sont symétriques et non cycliques  Je serais intéressé par la résolution que tu as faite du système. | |
|   | | tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Complexe. Sujet: Re: Complexe.  Sam 18 Déc 2010, 18:55 Sam 18 Déc 2010, 18:55 | |
| J'avais fait la même solution que celle de Dijkschneier , mais j'ai voulu trouver une autre , c'est pour ça que j'ai posté l'exercice.
En réessayant , j'ai pensé à utiliser un polynôme du troisième degré :
P(z)=z³+bz²+az+c qui a trois racines complexes x,y et z .
on a b=-(x+y+z) , a=xy+yz+xz et c =-xyz
d'où P(z)=z³-z²+az-1
on doit discuter les cas de a , peut-être utiliser Cardan .... reste à essayer.
j'ai aussi songé à utiliser l'implication |x|=|y|=|z|=1=>|xy+yz+xz|=|x+y+z|=1 (qui se démontre facilement) ainsi on aura |a|=1 alors a.ā=1 ..... j'ai pas pu finir .
| |
|   | | Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Complexe. Sujet: Re: Complexe.  Sam 18 Déc 2010, 19:03 Sam 18 Déc 2010, 19:03 | |
| - Dijkschneier a écrit:
- Oui Sporovitch. Les permutations à la fin sont symétriques et non cycliques

Je serais intéressé par la résolution que tu as faite du système. OK! Ouisin²a+sin²b+2sin(a)sin(b)=sin²(a+b) ==> 1-cos²a+1-cos²b+2cos(a)cos(b)+2sin(a)sin(b)=sin²(a+b)+2cos(a)cons(b)=1-cos²(a+b)+2cos(a)cos(b) ==> 1+2cos(a-b)+cos²(a+b)=(cos(a)+cos(b))²=(1-cos(a+b))² ce qui donne cos(a-b)+cos(a+b)=0 ou cos(a+b)=cons(pi-a+b)
Dernière édition par Sporovitch le Dim 19 Déc 2010, 00:16, édité 1 fois (Raison : fix a typo) | |
|   | | Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Complexe. Sujet: Re: Complexe.  Sam 18 Déc 2010, 19:58 Sam 18 Déc 2010, 19:58 | |
| - tarask a écrit:
- J'avais fait la même solution que celle de Dijkschneier , mais j'ai voulu trouver une autre , c'est pour ça que j'ai posté l'exercice.
En réessayant , j'ai pensé à utiliser un polynôme du troisième degré :
P(z)=z³+bz²+az+c qui a trois racines complexes x,y et z .
on a b=-(x+y+z) , a=xy+yz+xz et c =-xyz
d'où P(z)=z³-z²+az-1
on doit discuter les cas de a , peut-être utiliser Cardan .... reste à essayer.
j'ai aussi songé à utiliser l'implication |x|=|y|=|z|=1=>|xy+yz+xz|=|x+y+z|=1 (qui se démontre facilement) ainsi on aura |a|=1 alors a.ā=1 ..... j'ai pas pu finir .
ton idée est bonne aussi. je termine donc: z³-z²+az-1=0 ==> 1/z³ -1/z²-1/az -1=0 (a.ā=1) donc az=1+z²-z³ et 1/az=1+1/z²-1/z³ donc 1=(1+z²-z³)(1+1/z²-1/z³) <==> (z-1)²(z²+1)(z²+z+1)=0 CQFD. (les solution de : z²+z+1=0 ne vérifient pas lénnoncé initial) | |
|   | | tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Complexe. Sujet: Re: Complexe.  Sam 18 Déc 2010, 20:17 Sam 18 Déc 2010, 20:17 | |
| - Sporovitch a écrit:
- tarask a écrit:
- J'avais fait la même solution que celle de Dijkschneier , mais j'ai voulu trouver une autre , c'est pour ça que j'ai posté l'exercice.
En réessayant , j'ai pensé à utiliser un polynôme du troisième degré :
P(z)=z³+bz²+az+c qui a trois racines complexes x,y et z .
on a b=-(x+y+z) , a=xy+yz+xz et c =-xyz
d'où P(z)=z³-z²+az-1
on doit discuter les cas de a , peut-être utiliser Cardan .... reste à essayer.
j'ai aussi songé à utiliser l'implication |x|=|y|=|z|=1=>|xy+yz+xz|=|x+y+z|=1 (qui se démontre facilement) ainsi on aura |a|=1 alors a.ā=1 ..... j'ai pas pu finir .
ton idée est bonne aussi.
je termine donc:
z³-z²+az-1=0 ==> 1/z³ -1/z²-1/az -1=0 (a.ā=1)
donc az=1+z²-z³ et 1/az=1+1/z²-1/z³
donc 1=(1+z²-z³)(1+1/z²-1/z³) <==> (z-1)²(z²+1)(z²+z+1)=0
CQFD. (les solution de : z²+z+1=0 ne vérifient pas lénnoncé initial) très joli mon ami ! Je sentais bien la nécessité de devoir recourir au polynôme. Merci d'avoir complété ma réponse  | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Complexe. Sujet: Re: Complexe.  | |
| |
|   | | | | Complexe. |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
