| | Exercices de fonction: |  |
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Exercices de fonction: Sujet: Exercices de fonction:  Sam 01 Jan 2011, 13:19 Sam 01 Jan 2011, 13:19 | |
| Je vous propose cet exercice: f est une fonction définie de IR vers IR et satisfait pour tout x réél =f(x-1).f(x+5)) . Démontrez que f est périodique. Après quelques étapes, je me trouve bloqué ici .f(x-1)\big(1-f(x+5).f(x-4)\big)) pour tout réél x. Je n'arrive pas à continuer, car le quantificateur 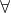 n'est pas distrubitif par rapport à "ou". Je demande une methode à résoudre l'exercice, ou bien une procédure afin de continuer ma preuve. J'ai une autre question: (le problème 2 page 230 du livre de l'analyse) f est une application définie de IR vers IR et qui satisfait, pour tout réél x: -f(x)\le) . -3f(x^3)\le) . Démontrez que f n'est pas injonctif. Le problème est que je ne sais pas ce qu'il faut mettre après le signe 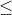 dans les deux coditions. Ainsi que, je ne sais pas s'ils veulent dire 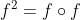 ou bien 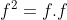 . Si quelqu'un a une idée, qu'il la partage avec moi, et merci d'avance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Mer 05 Jan 2011, 17:20 Mer 05 Jan 2011, 17:20 | |
| Toujours pas de réactions.
J'ai besoin de quelques idées.
| |
|
  | |
anas-az_137
Habitué
 Nombre de messages : 25 Nombre de messages : 25
Age : 31
Date d'inscription : 15/11/2010
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Mer 05 Jan 2011, 17:50 Mer 05 Jan 2011, 17:50 | |
| - nmo a écrit:
- Toujours pas de réactions.
J'ai besoin de quelques idées.
Bonsoir ..... 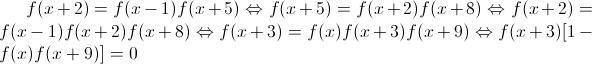 Si f(x + 3) = 0 , donc d'après la relation f(x + 2) = f(x-1)f(x+5) , on aura f(x) = f(x-3)f(x+3) , donc f(x) = 0 ,[tout nombre est période de f ].... si f(x+3)#0, donc : f(x)f(x+9) = 1 , f(x) = 1/f(x+9) , f(x+9) = 1/f(x+18) , On conclut Que : f(x) = f(x+18) , donc f est de période 18 .... | |
|
  | |
anas-az_137
Habitué
 Nombre de messages : 25 Nombre de messages : 25
Age : 31
Date d'inscription : 15/11/2010
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Mer 05 Jan 2011, 21:38 Mer 05 Jan 2011, 21:38 | |
| - Spoiler:
Si f(x + 3) = 0 , donc d'après la relation f(x + 2) = f(x-1)f(x+5) , on aura f(x) = f(x-3)f(x+3) , donc f(x) = 0....  9alo fin wdnak ajha ?
Remarque :  : le composé n-ième....  : f élevé à la puissance n ..... | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Mer 05 Jan 2011, 22:16 Mer 05 Jan 2011, 22:16 | |
| Voici une solution pr le 1er exercice : En posant x-1 à la place de x+2 nous obtenons f(x-1)=f(x-4).f(x+2) => (1) en posant x+5 à la place de x+2 on obtient f(x+5)=f(x-4).f(x+2==> (2) en multipliant (1) et (2) => f(x+5).f(x-1)=f(x+2)².f(x+  .f(x-4) d'où f(x+2).f(x+  .f(x-4)=1 d'autre part nous avons en remplacant x+2 par x+5 nous obtenons f(x+5)=f(x+2).f(x+  donc f(x-4).f(x+5)=1 d'où f(x)=1/f(x+9) d'ou f(x)=f(x+18) Donc f est périodique de période 18  CQFD | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Sam 08 Jan 2011, 18:45 Sam 08 Jan 2011, 18:45 | |
| - anas-az_137 a écrit:
- Remarque :
 : le composé n-ième.... : le composé n-ième....
 : f élevé à la puissance n ..... : f élevé à la puissance n ..... Merci de m'avoir répondu, cette notation réfère aussi à la n-dérivée de f. J'ai une remarque à faire sur la logique, et cela me rapelle ces paroles: - Dijkschneier a écrit:
- Soient P(x) et Q(x) deux propriétés définies sur E et dépendantes de la variable x.
Ce que je veux dire est très exactement que l'implication :

est fausse. Ce qui est aussi le cas des deux propositions de démonstration. Cordialement. | |
|
  | |
anas-az_137
Habitué
 Nombre de messages : 25 Nombre de messages : 25
Age : 31
Date d'inscription : 15/11/2010
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Sam 08 Jan 2011, 19:23 Sam 08 Jan 2011, 19:23 | |
| | |
|
  | |
anas-az_137
Habitué
 Nombre de messages : 25 Nombre de messages : 25
Age : 31
Date d'inscription : 15/11/2010
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Sam 08 Jan 2011, 20:08 Sam 08 Jan 2011, 20:08 | |
| - nmo a écrit:
- anas-az_137 a écrit:
- Remarque :
 : le composé n-ième.... : le composé n-ième....
 : f élevé à la puissance n ..... : f élevé à la puissance n ..... Merci de m'avoir répondu, cette notation réfère aussi à la n-dérivée de f.
J'ai une remarque à faire sur la logique, et cela me rapelle ces paroles:
- Dijkschneier a écrit:
- Soient P(x) et Q(x) deux propriétés définies sur E et dépendantes de la variable x.
Ce que je veux dire est très exactement que l'implication :

est fausse. Ce qui est aussi le cas des deux propositions de démonstration.
Cordialement. -Cela n'a rien a avoir avec ce que j'avais écrit , rapelle toi que j'ai traité deux cas .... a noter que [f(x+3) = 0 pour un certain x et 1 - f(x)f(x+9) = 0 pour d'autre valeur d'x n'a pas de sens a cause de 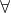 .... sauf erreur de ma part .... | |
|
  | |
nami.ne
Maître

 Nombre de messages : 118 Nombre de messages : 118
Age : 30
Date d'inscription : 05/10/2010
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Mar 11 Jan 2011, 12:43 Mar 11 Jan 2011, 12:43 | |
| pour le 1)
on f(x+2) = f(x-1).f(x+5) <=> f(x) = f(x-3) .f(x+3) **
et f(x+2) = f(x-1).f(x+5) <=>f(x) .f(x+6) =f(x+3)<=> f(x) = f(x+3)/f(x+6) *
De (**) et (*) on conclue que f(x-3) = 1/f(x+6) <=> f(x) = 1/f(x+9) <=>f(x+9) = 1/f(x)
f(x+2) = f(x-1).f(x+5) <=> f(x-3) = f(x-6) . f(x)
<=> f(x-6) = 1/f(x+3 ) <=> f(x-9) = 1/f(x)
on conclue alors des expressions soulignées que :
f(x-9) = f(x+9) <=> f(x) = f(x+18) ce qui donne f est périodique de T = 18
Mais une question est ce que faut que je montre que ( qq soit x£R / f(x) est non nul )
parce que comme vous voyez j'ai déjà divisé sur des f( x +a)
salamoâlaykom ^^
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Mar 11 Jan 2011, 16:49 Mar 11 Jan 2011, 16:49 | |
| La fonction nulle n'est pas périodique  Donc on peut la mettre en fraction  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 | |
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Mer 12 Jan 2011, 17:52 Mer 12 Jan 2011, 17:52 | |
| Car f(x)=f(x+€)=0 tel que € peut prendre toutes les valeurs possibles !! donc elle ne peut pa etre periodique  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Mer 12 Jan 2011, 17:58 Mer 12 Jan 2011, 17:58 | |
| - Mehdi.O a écrit:
- Car f(x)=f(x+€)=0 tel que € peut prendre toutes les valeurs possibles !!
donc elle ne peut pa etre periodique  Non, c'est faux. Une fonction est dite T-périodique, si il existe un T strictement positif tel que f(x+T)=f(x), dès que x, x+T, et x-T appartiennent à l'ensemble de définition de f. De cette définition, on conclut que la fonction nulle est périodique de période V0.25, ou 1, ou 2 ou ... Que penses-tu maintenant? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Sam 15 Jan 2011, 13:04 Sam 15 Jan 2011, 13:04 | |
| Oui je crois que tu as raison. Mais toutefois, la période de f n'est pas précise. Je veut dire la plus petite valeur.. Par contre, si on suppose que f est nulle cela mènera automatiquement au résultat voulu. Pour cela traitons les deux cas !!  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  Dim 16 Jan 2011, 15:57 Dim 16 Jan 2011, 15:57 | |
| - Mehdi.O a écrit:
- Par contre, si on suppose que f est nulle cela mènera automatiquement au résultat voulu.
Supposer que f est non nul, cela veut dire quoi au juste? Je suis hésitant entre les propositions suivantes: 1-Il existe un x réél, tel que f(x)#0. 2-Pour tout x réél, f(x)#0. Et j'aime savoir ce que tu veux dire. - nmo a écrit:
- J'ai une autre question: (le problème 2 page 230 du livre de l'analyse)
f est une application définie de IR vers IR et qui satisfait, pour tout réél x:
-f(x)\le) . .
-3f(x^3)\le) . .
Démontrez que f n'est pas injonctif.
Le problème est que je ne sais pas ce qu'il faut mettre après le signe 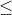 dans les deux coditions. dans les deux coditions.
Ainsi que, je ne sais pas s'ils veulent dire 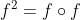 ou bien ou bien 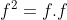 . .
Si quelqu'un a une idée, qu'il la partage avec moi, et merci d'avance. En tenant compte des autres exercices, on voit clairement que pour le premier aisi que pour le troisième, ils ont mis 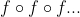 au lieu de 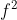 ou 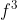 ou ... Donc, à un pourcentage plus élevé, ils veulent dire 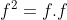 et 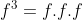 . P.S: Si quelqu'un aura une autre version du livre où cet exercice est bien rédigé, il serait gentil de sa part de me partager l'énoncé en question. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Exercices de fonction: Sujet: Re: Exercices de fonction:  | |
| |
|
  | |
| | Exercices de fonction: |  |
|
