| | Une bonne série d'exercices d'olympiade |  |
|
|
| Auteur | Message |
|---|
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Une bonne série d'exercices d'olympiade Sujet: Une bonne série d'exercices d'olympiade  Lun 17 Jan 2011, 10:55 Lun 17 Jan 2011, 10:55 | |
| Problème1:Posons ^2+a_{k}^2})) ) tel que  sont des réels strictement positifs et  . montrer qu'il existe un seul entier naturel n tel que 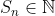 . Problème2:Soit a, b et c des réels tel que: 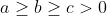 M.Q: 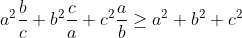 Problème3: Problème3: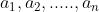 sont des nombres de  . M.Q: ^2})+\sqrt{a_{n}^2+(1-a_{1})^2}\geq%20\frac{n\sqrt{2}}{2}) problème4: problème4:Soit n un élément de 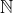 tel que 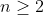 et 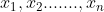 et 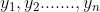 sont des nombres réels tel que: %20&%20&%20&%20\\%20y_{i+1}=E\left%20(%20\frac{n}{x_{i+1}}%20\right%20)%20&%20&%20&%20\end{matrix}\right.) M.Q: }=E(\sqrt{n})) On note E(x) la partie entière de x. Problème5:considérons l'application 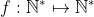 tel que =E(1+\frac{1}{2}+.....+\frac{1}{n})) . Montrer que f est surjectif. Problème6:Soit a, b et c les longueurs des côtés d'un triangle. Posons R=a²+b²+c² et S=(a+b+c)² Montrer que l'ensemble de la valeur de R/S est [1/3;1/2[. A vos stylos. | |
|
  | |
medamine.
Habitué
 Nombre de messages : 19 Nombre de messages : 19
Age : 29
Date d'inscription : 18/10/2010
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Lun 17 Jan 2011, 12:44 Lun 17 Jan 2011, 12:44 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Mar 18 Jan 2011, 18:27 Mar 18 Jan 2011, 18:27 | |
| TJRS pas de réponses  | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Mar 18 Jan 2011, 19:04 Mar 18 Jan 2011, 19:04 | |
| - ali-mes a écrit:
- Problème5:
considérons l'application 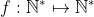 tel que tel que =E(1+\frac{1}{2}+.....+\frac{1}{n})) . .
Montrer que f est surjectif.
Solution au problème 5 :^ Il suffit de montrer que =k) Soit 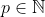 et soit g l'application de 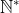 vers  telle que =\sum_{k=1}^{n}\frac{1}{k}) Nous avons : \succeq%20\frac{1}{1}+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+...+\frac{2^{p-1}}{2^p}=1+\frac{1}{2}+\frac{1}{2}+...+\frac{1}{2}=1+\frac{p}{2}) Et nous avons =E(g(n))) Donc \geq%20E(1+\frac{p}{2})) (1) Et puis 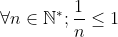 Ce qui fait que =f(n)) ou =f(n)+1) (2) De (1) et de (2), concluons. Sauf erreur. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Mar 18 Jan 2011, 21:00 Mar 18 Jan 2011, 21:00 | |
| | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Mar 18 Jan 2011, 21:02 Mar 18 Jan 2011, 21:02 | |
| Mais pour quoi ca ne marche pas le latex?! je vais ecrire ce que j'ai trouve manuellement et je l'envoierai.merci d'abord pour ces exercices.. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Mar 18 Jan 2011, 21:06 Mar 18 Jan 2011, 21:06 | |
| Les problèmes sont bons.
Le premier se fait en montrant tout d'abord que S_n = sqrt(n^4 + 17^2) (Minkowski) puis en montrant que n^4+17^2 est un carré parfait si et seulement si n=12 (triplet pythagoricien).
Le deuxième est classique.
Le troisième se fait en utilisant successivement Minkowski et Cauchy-Schwarz.
Le quatrième : es-tu sûr de la définition de y_(i+1) ?
Le cinquième consiste à prouver que pour tout entier m, il existe un entier n tel que E(1 + 1/2 + 1/3 + ... + 1/n) = m. Il suffit de faire une récurrence sur m et d'utiliser l'encadrement ln(n+1) <= 1 + 1/2 + 1/3 + ... + 1/n <= ln(n) + 1
Le sixième problème est enfin classique.
J'aimerais bien connaître la source de tes problèmes.
Dernière édition par Dijkschneier le Mer 19 Jan 2011, 12:58, édité 1 fois | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Mar 18 Jan 2011, 21:56 Mar 18 Jan 2011, 21:56 | |
| Pouvez vous nous montrer la solution du 3eme? | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Mar 18 Jan 2011, 22:16 Mar 18 Jan 2011, 22:16 | |
| - Dijkschneier a écrit:
- Les problèmes sont bons.
Le premier se fait en montrant tout d'abord que S_n = sqrt(n^4 + 17^2) (Minkowski) puis en montrant que n^4+17^2 est un carré parfait si et seulement si n=12 (triplet pythagoricien).
Le deuxième est classique.
Le troisième se fait en utilisant successivement Minkowski et Cauchy-Schwarz.
Le quatrième : es-tu sûr de la définition de y_(i+1) ?
Le cinquième consiste à prouver que pour tout entier m, il existe un entier n tel que E(1 + 1/2 + 1/3 + ... + 1/n) = m. Il suffit de faire une récurrence sur m et de distinguer deux cas.
Le sixième problème est enfin classique.
J'aimerais bien connaître la source de tes problèmes. DES solutions détaillés SVP Et pour la source = c'est secret !   et pour la définition de y_(i+1) = elle est juste | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Mar 18 Jan 2011, 22:26 Mar 18 Jan 2011, 22:26 | |
| P.S=les exos que j'ai propsé (sauf 5) ont une relation avec : Majorant et minorant d'une partie de IR | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Mer 19 Jan 2011, 12:35 Mer 19 Jan 2011, 12:35 | |
| - ali-mes a écrit:
- DES solutions détaillés SVP
Non. Les grandes lignes sont suffisantes. Lorsque je dis Minkowski, c'est qu'il faut l'appliquer directement. Je n'ai aucune raison de développer davantage. - ali-mes a écrit:
- et pour la définition de y_(i+1) = elle est juste
Alors la suite (y_n) n'a plus aucune raison d'être définie. Il y a un truc compliqué dans ce quatrième problème, car si l'on tentait une récurrence sur n, on ne pourrait pas commencer par dire que %20=%20Min(Min_{1\leq%20i\leq%20n} (x_i),%20x_{n+1})) , car x_i change de sens en fonction de n (x_1 change à chaque fois selon n). | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Mer 19 Jan 2011, 12:50 Mer 19 Jan 2011, 12:50 | |
| | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  Sam 22 Jan 2011, 22:04 Sam 22 Jan 2011, 22:04 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Une bonne série d'exercices d'olympiade Sujet: Re: Une bonne série d'exercices d'olympiade  | |
| |
|
  | |
| | Une bonne série d'exercices d'olympiade |  |
|
