abdelbaki.attioui
Administrateur
 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 | | Sujet: Problème février 2011 Lun 31 Jan 2011, 11:06 | |
| Soit f : R ---> R dérivable. On suppose qu'il existe c dans R tel que  pour tout (a,b) dans R² . Montrer que f ' (c)=0 | |
|
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Problème février 2011 Sam 09 Aoû 2014, 13:32 | |
| - abdelbaki.attioui a écrit:
- Soit f : R ---> R dérivable. On suppose qu'il existe c dans R tel que
pour tout (a,b) dans R² . Montrer que f ' (c)=0 Je propose une solution: On pose : F(x)=\int^{x}(f(t)-f(c))dt) . Si 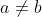 , l'hypothèse implique que \neq F(b)) . Donc 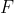 est injective. Continue et injective, un lemme connu fournit que 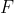est monotone. On a donc: : F'(x)\ge 0) ou : F'(x)\le 0) . Si , alors : f(x)-f(c)\ge 0) . On pose: : g(x)=f(x)-f(c)) . On a 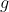 est dérivable et admet un minimum absolu en  , donc =0) . Ce qui équivaut à =0) , comme voulu. L'autre cas se traite de la même façon, et fournit le même résultat. CQFD. Sauf erreurs. | |
|
