qlqn peut démontrer que..???

Habitué Nombre de messages : 14 Age : 31 Date d'inscription : 02/12/2010

vous peuvez demontre ceci??
x^y=d <=> (x/d)^(y/d)=1

j'essayais mais j'ai démontré seulement une implication:

- x^y=d => d/x et d/c
=> 1/ (d/x) et 1/ (d/y)
=> 1/ ( (x/d)^(y/d) )

il me reste de démonter l'autre implication: ( (x/d)^(y/d) ) /1

merci d'avance!!

Expert sup Nombre de messages : 1693 Age : 68 Date d'inscription : 17/11/2008

salam

on travaille dans IN

x^y = d
====> x= d.x' et y =dy'

Supposons que k soit un diviseur commun à x'=x/d et y'= y/d

=====> x = dkx" et y = dky"

=====> dk diviseur commun à x et y ===> dk divise d ( le plus grand) ===> k=1

donc (x/d)^(y/d) = 1

_________________________

réciproquement

soit d un diviseur com à x et y tel que (x/d)^(y/d) = 1

posons D = x^y ====> d divise D ===> D=kd

x/d = Dx'/d = kx'
y/d = Dy'/d = ky'

(x/d)^(y/d)=1 ===> kx'^ky'=1 ====> k.(x'^y') = 1 ===> k=1 et (x'^y')=1

===> D=d ====> x^y = d

____________________________________

Habitué Nombre de messages : 14 Age : 31 Date d'inscription : 02/12/2010

merci "houssa" tu m'as aidé. Wink

Maître Nombre de messages : 234 Age : 31 Date d'inscription : 24/10/2009

Il y a une démonstration avec le théorème fondamental de l'arithmétique.
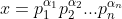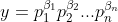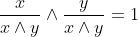On pose $qlqn peut démontrer que..??? Gif.latex?x=p_1^{\alpha%20_1}p_2^{\alpha_2}..$ et $qlqn peut démontrer que..??? Gif.latex?y=p_1^{\beta%20_1}p_2^{\beta_2}..$
On a $qlqn peut démontrer que..??? Gif.latex?x\wedge%20y=p_1^{min(\alpha_1,\beta_1)}p_2^{min(\alpha_2,\beta_2)}..$
Donc :
$qlqn peut démontrer que..??? Gif.latex?\frac{x}{x\wedge%20y}\wedge%20\frac{y}{x\wedge%20y}=p_1^{min(\alpha_1-min(\alpha_1,\beta_1),\beta_1-min(\alpha_1,\beta_1))}p_2^{min(\alpha_2-min(\alpha_2,\beta_2),\beta_2-min(\alpha_2,\beta_2))}..$
Il est clair que $qlqn peut démontrer que..??? Gif$ de ce fait, $qlqn peut démontrer que..??? Gif$
Sauf erreur.
Au plaisir ! Smile

Expert sup Nombre de messages : 817 Age : 31 Date d'inscription : 31/10/2009

On peut aussi procéder par l'absurde , mais bon pas la peine de sortir les mitralleuse pour des mouches :p

Habitué Nombre de messages : 14 Age : 31 Date d'inscription : 02/12/2010

Mr, "houssa" j'ai bien compris mais je voulais juste te poser une question: est ce que c'est obligatoire que (x,y) doit être dans IN ??

ils ne peuvent pas être dans Z*???

_________________________________________________________________________

Expert sup Nombre de messages : 1482 Age : 30 Date d'inscription : 12/12/2009

@mizmaz : je te propose de réfléchir sur le dernier problème du marathon de première (problème 64) qui peut être résolu avec une logique semblable à celle que tu as utilisée dans ce problème.

Habitué Nombre de messages : 14 Age : 31 Date d'inscription : 02/12/2010

Tu peut me donner l'URL auquel ce probleme est résolu???

Expert sup Nombre de messages : 1693 Age : 68 Date d'inscription : 17/11/2008

salam

pour foxmath

il suffit de travailler dans IN

car :

x^y = |x|^y = x^|y| = |x|^|y|

et (kx)^(ky) = |k|.(x^y)

___________________________________________________

pour mizmaz

pourquoi tu as pris les mêmes diviseurs premiers pour x et y : p1 , p2 , ........, pn

________________________________________

Habitué Nombre de messages : 27 Age : 39 Date d'inscription : 04/03/2011

and.it.webobo.biz

mercii je pense donc ,je suis

» qui peut demontrer cette limite!!!!????
» DEmontrer QUe...
» demontrer !!!!!!!!!!!!!!!!
» demontrer que
» demontrer que ...............