un morphisme et une matrice.

Bonsoir,

Considérons une application f , définie par :



A) déterminer une loi de composition interne 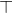sur pour que f soit un homomorphisme de (, T) vers IM2()

B) Considérons l'ensemble E , défini par :



1) Déterminer l'élement neutre sur (,×)
2) soit un élement de * . Trouver le symétrique de la matrice sur (,×) .


( Al Moufid (Algèbre) , exercice 59 page 218)

.

IM2(IR) est l'ensemble des matrices carrées 2x2 muni de l'addition matricielle ?
Dans ce cas, la loi interne dans A) c'est l'addition naturelle dans IR.

Juste une question , quelle est la différence entre un morphisme et un homomorphisme ?

Sinon , oui l'addition fera l'affaire.
Pour le reste c'est juste calculatoire. Si on note un élément de E par M(x) il me semble que l’élément neutre est M(1/2) et un symétrique de Mx est M(1/(4x)).
j'ai bien dit un et non le Car a priori rien ne dit que c'est un groupe , à toi de montrer l'unicité.

On parle d'homomorphisme lorsque l'on veut préciser que c'est un morphisme entre groupes.
Et je ne comprends pas ce qui pose problème dans cet exercice puisqu'il me semble assez immédiat.