inégalité

Soient a, b et c trois réels strictement positifs tel que 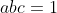$inégalité Gif$

Montrer que :

$inégalité Gif$

Féru Nombre de messages : 67 Age : 30 Date d'inscription : 28/02/2011

Pose :a=x^3 , b=y^3 et c=z^3 ( xyz=1 ) et utilise ces 2 inégalités : ( IAG )
x^3/(y^3+1)(x^3+1) +( y^3+1) /8 +(x^3+1)/8 > 3x/4
x^3+y^3+z^3 >3 , x+y+z > 3 , et tu obtiendras le résultat !

Voici ma méthode:

L'inégalité à démontrer est équivalente à: $inégalité Gif$

$inégalité Gif$

$inégalité Gif$

$inégalité Gif$

$inégalité Gif$

Posons $inégalité Gif$

L'inégalité à démontrer est équivalente à $inégalité Gif$

$inégalité Gif$

$inégalité Gif$

$inégalité Gif$

Ce qui est vrai d'après IAG. ( $inégalité Gif$ )

D'où le résultat voulut.

Expert grade2 Nombre de messages : 345 Age : 29 Date d'inscription : 28/01/2010

ali-mes a écrit:: Voici ma méthode:

L'inégalité à démontrer est équivalente à: $inégalité Gif$

$inégalité Gif$

$inégalité Gif$

$inégalité Gif$

$inégalité Gif$

Posons $inégalité Gif$

L'inégalité à démontrer est équivalente à $inégalité Gif$

$inégalité Gif$

$inégalité Gif$

$inégalité Gif$

Ce qui est vrai d'après IAG. ( $inégalité Gif$ )

D'où le résultat voulut.

Bien joué belle méthode !

hhhhhh!! je ne sais pas si c'est au hasard que j'ai trouvé mais voici un lien qui explique toute la demonstration:
https://www.youtube.com/watch?v=CffzB8MuSSo
il dit que une inégalité aux olympiades est comme un plat de résistance au réstaurant!!!

Voilà d'où j'ai tiré cet exo: https://mathsmaroc.jeun.fr/t16497p90-preparations-aux-olympiades-de-premiere-2010-2011

j'ai pas parler comme ça pour te sousestimé et je ne le ferais jamais mais c juste la surprise qui m'a pouusé. en plus j'ai trouvé l'exo très élegant.
Merci de t'as part Very Happy

En tous cas, je vous propose cette inégalité: (Own)

Soient a, b et c trois nombres réels strictement positifs.

Montrer que: $inégalité Gif$

ENJOY ....

Elle est tres difficile...(pr moi))pr vous je sais bien ke c'est facile)

ali-mes a écrit:: En tous cas, je vous propose cette inégalité: (Own)
Soient a, b et c trois nombres réels strictement positifs.
Montrer que: $inégalité Gif$
ENJOY ....

On a selon l'inégalité arithmético-géométrique: $inégalité Gif.latex?\frac{a}{b}+\frac{b}{a+c}+\frac{c+a}{a}\geq3$ .
Donc $inégalité Gif$ .
Donc $inégalité Gif$ .
Soit au final $inégalité Gif$ .
Sauf erreur.

Excellent nmo.

C'était la première inégalité que j'ai créé (juste il faut jouer avec les variables)...

J'invite quelqu'un à poster une inégalité à condition qu'elle soit facile un peu et qui nécessite pas d'utiliser Jensen ou Minkowski (ou autres inégalités qui font peur Smile

) ...... Puisque la plupart de nous sont des débutant (je parle de moi-même sincèrement) et ne connaissent que quelques inégalités de base (IAG, CS, I.triangulaire, ...... )

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

a , b , et c sont les longueurs des trois côtés d'un triangle.
Montrez que 0 =< 0 a²b(a - b ) + b²c( b - c ) + c²a( c - a ) . .elle est facile Very Happy

http://www.artofproblemsolving.com/Forum/resources.php?c=1&cid=16&year=1983

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

Essaie de prouver Very Happy

( ne triche po Surprised

)

Je connais cette inégalité avant que tu l'as posté ..... donc à mon avis, C'est pas la peine de poster une réponse si elle déjà existe sur MATHLINKS .... L'astuce de cet exo est la substitution de Ravi et il y a beaucoup de réductions ... donc il faut être un peu précis. Et à la fin, tu auras une laborieuse application de l'inégalité de Cauchy Schwartz .....

Boubou maths, postes une autre ....

P.S: On sait tous chercher dans Mathlinks Smile

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

soit a,b,c,d,e de IR tel que a+b+c+d+e=8 et a²+b²+c²+d²+e²=16
trouver la valeur maximale de e

Soit $inégalité Gif$ l'ensemble des valeurs de $inégalité Gif$ .
(On cherche $inégalité Gif$ )

On a d'après l'inégalité de Cauchy Schwartz:

$inégalité Gif$

$inégalité Gif$

$inégalité Gif$

$inégalité Gif$

$inégalité Gif$

Donc $inégalité Gif$ est un majorant de $inégalité Gif$ .

Maintenant, nous allons montrer que: $inégalité Gif$ . Donc il suffit de chercher des valeurs pour $inégalité Gif$
tel que $inégalité Gif$ . Et cela est vérifie en prenant $inégalité Gif$ .

Donc $inégalité Gif$ .

D'où le résultat voulut.

J'attends toujours vos remarques et questions ...

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

t'as réponse est correcte , veuillez poster une autre Very Happy

J'ai rien dans ma tête ....

Que chacun sent libre pour poster une inégalité.

salut

EXO 1 (trés facile)
x et y des réels strictement positifs
M.Q $inégalité Gif$

EXO 2 (pas facile)
soit x , y et z des réels différents 1 tel que xyz=1
M.Q $inégalité Gif$

Pour le 2eme exo:

contre-exemple: prends x=y=z=0

Et pour le premier: Application directe de IAG.

dsl
pour le 2eme exo c'est xyz=1

Maître Nombre de messages : 139 Age : 30 Date d'inscription : 26/02/2011

abdelkrim-amine a écrit:: salut

EXO 1 (trés facile)
x et y des réels strictement positifs
M.Q $inégalité Gif$

On peut aussi minorer la valeur en utilisant , " le carré est toujours positif " x^2 +y^4 > 2x²y

» inegalité
» Inégalité 02
» INEGALITE
» une inégalité
» Inegalite 00