|
| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants | |
| Auteur | Message |
|---|
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 | |   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 16:57 Dim 31 Oct 2010, 16:57 | |
| Problème 22 : ET abc =1
Dernière édition par Mehdi.O le Mer 17 Nov 2010, 14:26, édité 1 fois | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 17:28 Dim 31 Oct 2010, 17:28 | |
| @Mehdi.O : et tes messages précédents au sujet desquels je t'ai fait une remarque, tu vas les supprimer ? | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 17:39 Dim 31 Oct 2010, 17:39 | |
| Comment supprimer un message? | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 17:47 Dim 31 Oct 2010, 17:47 | |
| - Mehdi.O a écrit:
- Comment supprimer un message?
Avant de participer, il faut lire ces conditions: - Citation :
- Comme l'évolution de l'âge est irrémédiable, et que le marathon consacré à la préparation des olympiades de seconde touche à sa fin, j'aimerais, en restant dans la même lancée, proposer d'entamer un nouveau marathon qui cette fois-ci sera conçu pour préparer les olympiades de première.
Un peu à la manière de tous les marathons, celui-ci aurait des règles qui ne sortent pas du commun :
- Dans l'idéal, chaque participant ayant donné une solution à un précédent problème doit se charger de proposer un nouveau problème. Si quelqu'un qui répond à un problème n'a pas de nouveau problème à proposer, qu'il l'indique clairement ! D'autres s'en chargeront, si possible.
- Numéroter clairement les problèmes, et citer le numéro du problème dans la solution que l'on en donne.
- Ne pas poster de solutions incomplètes et par conséquent, ne pas attendre de confirmation pour reproposer un nouveau problème.
- Favoriser l'entente et la bonne humeur. Tu doit édité tes deux derniers message oû tu as postulé de nouveau problémes. Il y a dejà deux problémes non resolu. Maniére de les conservé, et les postulé au bonnes moments. (Voir ce qui est en bleu) | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 18:53 Dim 31 Oct 2010, 18:53 | |
| D'accord veuillez m'excuser ! | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 22:24 Dim 31 Oct 2010, 22:24 | |
| - Mehdi.O a écrit:
- D'accord veuillez m'excuser !
Tu dis que tu t'excuses mais tu ne t'appliques pas. As-tu supprimé tes messages ? Pour supprimer un message, il faut les éditer et les vider de leur contenu (ne laisser qu'un point). | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 01 Nov 2010, 17:25 Lun 01 Nov 2010, 17:25 | |
| - Dijkschneier a écrit:
- nmo a écrit:
- Dijkschneier a écrit:
- Problème 17 :
Soit ABC un triangle et D le pied de la bissectrice intérieure de l'angle A.
Montrez que : AD² = AB.AC - BD.CD. Selon le théorèmer des bissectrices intérieures, on a ^2\bigg)) . ==>(1) . ==>(1)
Merci de prouver cette relation car on ne voit pas d'où ça peut venir.
Le théorème classique de la bissectrice nous permet de dire que : BD/DC = AB/AC. Voilà le lien pour la solution: https://mathsmaroc.jeun.fr/seconde-tronc-commun-f6/bissectrice-d-un-angle-t13210.htm. Bonne découverte. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 01 Nov 2010, 17:30 Lun 01 Nov 2010, 17:30 | |
| - Dijkschneier a écrit:
- nmo a écrit:
Donc +k_{n-1}(a^{n-1}+b^{n-1}+c^{n-1})+k_{n-2}(a^{n-2}+b^{n-2}+c^{n-2})+...+k_{1}(a+b+c)+3k_{0}=a+b+c) . .
Donc 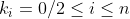 , , 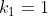 , et , et 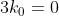 . .
Et ainsi 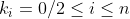 , , 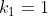 , et , et 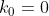 . .
Non ! Ce n'est pas une égalité polynomiale !! C'est quoi donc à ton avis? Si on traite chaque cas séparément, on se ramène à  . Et puis P(a)=0, P(b)=0, et P(c)=0. Ainsi on trouve que a=b=c=0. J'attends ton avis. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 01 Nov 2010, 17:43 Lun 01 Nov 2010, 17:43 | |
| - Mehdi.O a écrit:
- Problème 22 :
 C'est faux, prends a=b=c=1/2. Rapelle-toi de ces paroles: - Dijkschneier a écrit:
- Ceci est un marathon. Merci de ne pas l'inonder de 1000 problèmes alors que les problèmes précédents n'ont pas encore été résolus.
Il reste encore un tas de problèmes sans solutions confirmés, les voici: - Dijkschneier a écrit:
- Problème 14 :
Soient E et F deux ensembles et f une application définie sur E et à valeurs dans F.
Montrer que : f bijective <=> %20:%20F%20-%20f(X)%20=%20f(E-X)) - Dijkschneier a écrit:
- Problème 18 :
Soit P un polynôme à coefficients entiers. On suppose qu’il existe trois entiers a, b et c tels que
P(a) = b, P(b) = c et P(c) = a. Montrer que a = b = c.
Problème 19 :
Soit P un polynôme de degré 2008 tel que P(k)=1/k pour tout k appartenant à {1,2,3,...,2009}. Calculer P(0). - nmo a écrit:
- Problème 20:
- Dijkschneier a écrit:

Soient (D) et (Delta) deux droites parallèles du plan, et soient E et F deux points distincts des deux droites, et tels que E soit du côté de (D), et F de celui de (Delta). Trouver le ou les emplacements des deux points K et H de (D) et (Delta) respectivement qui minimisent la somme EK²+KH²+HF² et tels que (KH) soit perpendiculaire aux deux droites (D) et (Delta).
Bonne chance. Veille à ne pas proposer un autre exercice, avant que ceux-ci ne soient pas encore résolus Cela nuit à la présentation du sujet qui se voit maintenant en ruine. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 01 Nov 2010, 19:41 Lun 01 Nov 2010, 19:41 | |
| @Mehdi.O : Merci ! - nmo a écrit:
Voilà le lien pour la solution:
https://mathsmaroc.jeun.fr/seconde-tronc-commun-f6/bissectrice-d-un-angle-t13210.htm.
Bonne découverte. D'accord ! - nmo a écrit:
C'est quoi donc à ton avis?
Si on traite chaque cas séparément, on se ramène à  . .
Et puis P(a)=0, P(b)=0, et P(c)=0.
Ainsi on trouve que a=b=c=0.
J'attends ton avis. On ne peut faire l'identification des coefficients que lorsque nous sommes confrontés à une égalité polynomiale, i.e, une égalité vraie pour toute variable x de IR. Je ne comprends pas ce que tu me dis. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 03 Nov 2010, 11:10 Mer 03 Nov 2010, 11:10 | |
| - Dijkschneier a écrit:
- On ne peut faire l'identification des coefficients que lorsque nous sommes confrontés à une égalité polynomiale, i.e, une égalité vraie pour toute variable x de IR.
Je ne comprends pas ce que tu me dis. C'est quoi donc une égalité polynomiale. En tout cas, je renonce. (En effet, je ne trouve ni la solution de 14, ni celle de 18, ni celle de 19) Je vois bien qu'il est temps de présenter les solutions des exercices, pour faire avancer le jeu. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 03 Nov 2010, 13:36 Mer 03 Nov 2010, 13:36 | |
| - nmo a écrit:
C'est quoi donc une égalité polynomiale.
En tout cas, je renonce.
Je l'ai dit : c'est une égalité vraie pour tout x appartenant à l'ensemble (l'anneau) de définition du polynôme. Solution au problème 14 :Soit f une fonction définie sur E et à valeurs dans F. - Supposons que f est bijective. Soit X une partie de E. * Soit ) , et montrons que ) . %20\Rightarrow%20\exists%20%20x%20\in%20(E-X)%20:%20f(x)=y) Et on a : %20\Leftrightarrow%20y\notin%20f(X)) . Supposons par l'absurde que ) . Alors =f(x)) . Et étant donné que f est bijective, donc injective, il vient que x=x', et par conséquent, 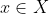 . Et cela est clairement une contradiction. * Soit ) , et montrons que ) . Assez facile. - Supposons que =f(E-X)) . * f est surjective en posant X égal à l'ensemble vide. * f est injective, et c'est le point le plus intéressant du problème : En effet, soient a et b de E tels que f(a)=f(b), et supposons par l'absurde que a est différent de b. En posant successivement X={a} puis \})) , on obtient les deux relations : %20=%20f(E-\{a\})%20\\%20F%20-%20f(f^{-1}(\{f(a)\}))=%20f(E-f^{-1}(\{f(a)\}))%20\end{cases}) \}%20=%20f(E-\{a\})%20\\%20F%20-%20\{f(a)\}=%20f(E-f^{-1}(\{f(a)\}))%20\end{cases}) %20=%20f(E-f^{-1}(\{f(a)\}))) Maintenant, b étant différent de a, on a %20\in%20f(E-\{a\})%20\Rightarrow%20f(b)%20\in%20f(E-f^{-1}(\{f(a)\}))%20\Rightarrow%20(\exists%20x%20\in%20E-f^{-1}(\{f(a)\})%20:%20f(x)=f(b)%20\Rightarrow%20\exists%20x%20\in%20E%20:%20f(x)\notin\{f(a)\}%20\text{%20et%20}%20f(x)=f(b)%20\Rightarrow%20\exists%20x%20\in%20E%20:%20f(x)\neq%20f(a)%20\text{%20et%20}%20f(x)=f(b)%20\Rightarrow%20f(a)%20\neq%20f(b)) . Et cela constitue une contradiction. Solution au problème 18 :Ce problème est classique et est fondé sur le lemme suivant : "Si P est un polynôme à coefficients entiers, alors pour tous entiers a et b, (a-b) divise (P(a)-P(b)). " Revenons au problème. Supposons par symétrie des rôles que a>=b>=c. On a donc, d'une part : a-b divise P(a)-P(b), donc a-b divise b-c. Et d'autre part, b-c divise P(b)-P(c), donc b-c divise c-a. On en déduit que a-b divise c-a. Or c-a divise a-b, car c-a divise P(c)-P(a), donc c-a divise a-b. Par conséquent, |a-b|=|c-a|, et donc : a-b = a-c, b=c. Et on prouve de même que |b-c|=|a-c|, et |a-b|=|b-c|. On en déduit finalement que a=b=c. Solution au problème 19 :On introduit le polynôme H(x)=xP(x) - 1 sur lequel on va travailler. P est de degré 2008, H est donc de degré 2009. De plus, H(1)=H(2)=...=H(2009)=0. Mais alors, H peut s'écrire, selon le théorème de d'Alembert-Gauss, comme produit de polynômes du premier degré : H(x)=k(x-1)(x-2)...(x-2009). De plus, d'après la définition de H, on a que H(0)=-1. Donc : -1 = -k 2009!, donc  , où ! désigne la factorielle. Ainsi : %20=%20\frac{1}{2009!}(x-1)(x-2)\cdots(x-2009)) . Enfin, en développant H grâce aux formules de Viète, et en établissant l'égalité des coefficients de part et d'autres de la relation H(x)=xP(x)-1, on arrive à déterminer explicitement P. On peut alors calculer P(0).
Dernière édition par Dijkschneier le Mar 16 Nov 2010, 13:19, édité 2 fois | |
|   | | Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 03 Nov 2010, 13:50 Mer 03 Nov 2010, 13:50 | |
| C'est un exercice intéressant sur une caractérisation de la bijection. L'idée de construction de l'injectivité est bonne.
Juste une petite question , pour f(f^[-1]({f(a)}))={f(a)}. As-tu utilisé la surjectivité de f ?
Merci. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 03 Nov 2010, 14:09 Mer 03 Nov 2010, 14:09 | |
| Merci Othmaann. Non, la surjectivité n'a pas été utilisée lors de ce passage. Faire l'image réciproque d'un singleton dont l'élément admet un antécédent, puis l'image directe du résultat obtenu, nous ramène à ce même singleton. Cela se démontre. | |
|   | | Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 03 Nov 2010, 14:21 Mer 03 Nov 2010, 14:21 | |
| Parfait.De même pour le reste! | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 03 Nov 2010, 15:21 Mer 03 Nov 2010, 15:21 | |
| - Dijkschneier a écrit:
- nmo a écrit:
C'est quoi donc une égalité polynomiale.
En tout cas, je renonce.
Je l'ai dit : c'est une égalité vraie pour tout x appartenant à l'ensemble (l'anneau) de définition du polynôme.
Solution au problème 14 :
Soit f une fonction définie sur E et à valeurs dans F.
- Supposons que f est bijective.
Soit X une partie de E.
* Soit ) , et montrons que , et montrons que ) . .
%20\Rightarrow%20\exists%20%20x%20\in%20(E-X)%20:%20f(x)=y)
Et on a : %20\Leftrightarrow%20y\notin%20f(X)) . .
Supposons par l'absurde que ) . Alors . Alors =f(x)) . Et étant donné que f est bijective, donc injective, il vient que x=x', et par conséquent, . Et étant donné que f est bijective, donc injective, il vient que x=x', et par conséquent, 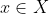 . Et cela est clairement une contradiction. . Et cela est clairement une contradiction.
* Soit ) , et montrons que , et montrons que ) . .
Assez facile.
- Supposons que =f(E-X)) . .
* f est surjective en posant X égal à l'ensemble vide.
* f est injective, et c'est le point le plus intéressant du problème :
En effet, soient a et b de E tels que f(a)=f(b), et supposons par l'absurde que a est différent de b.
En posant successivement X={a} puis \})) , on obtient les deux relations : , on obtient les deux relations :
%20=%20f(E-\{a\})%20\\%20F%20-%20f(f^{-1}(\{f(a)\}))=%20f(E-f^{-1}(\{f(a)\}))%20\end{cases})
\}%20=%20f(E-\{a\})%20\\%20F%20-%20\{f(a)\}=%20f(E-f^{-1}(\{f(a)\}))%20\end{cases})
%20=%20f(E-f^{-1}(\{f(a)\})))
Maintenant, b étant différent de a, on a %20\in%20f(E-\{a\})%20\Rightarrow%20f(b)%20\in%20f(E-f^{-1}(\{f(a)\}))%20\Rightarrow%20(\exists%20x%20\in%20E-f^{-1}(\{f(a)\})%20:%20f(x)=f(b)%20\Rightarrow%20\exists%20x%20\in%20E%20:%20f(x)\notin\{f(a)\}%20\text{%20et%20}%20f(x)=f(b)%20\Rightarrow%20\exists%20x%20\in%20E%20:%20f(x)\neq%20f(a)%20\text{%20et%20}%20f(x)=f(b)%20\Rightarrow%20f(a)%20\neq%20f(b)) . .
Et cela constitue une contradiction.
Solution au problème 18 :
Ce problème est classique et est fondé sur le lemme suivant :
"Si P est un polynôme à coefficients entiers, alors pour tous entiers a et b, (a-b) divise (P(a)-P(b)). "
Revenons au problème.
On a donc, d'une part : a-b divise P(a)-P(b), donc a-b divise b-c.
Et d'autre part, b-c divise P(b)-P(c), donc b-c divise c-a.
On en déduit que a-b divise c-a.
Or c-a divise a-b, car c-a divise P(c)-P(a), donc c-a divise a-b.
Par conséquent, a-b=c-a, et donc : 2a = b+c.
Et on prouve de même que 2b = a+c, et 2c=a+b.
On en déduit facilement que a=b=c.
Solution au problème 19 :
On introduit le polynôme H(x)=xP(x) - 1 sur lequel on va travailler.
P est de degré 2008, H est donc de degré 2009.
De plus, H(1)=H(2)=...=H(2009)=0.
Mais alors, H peut s'écrire, selon le théorème de d'Alembert-Gauss, comme produit de polynômes du premier degré : H(x)=k(x-1)(x-2)...(x-2009).
De plus, d'après la définition de H, on a que H(0)=-1.
Donc : -1 = -k 2009!, donc  , où ! désigne la factorielle. , où ! désigne la factorielle.
Ainsi : %20=%20\frac{1}{2009!}(x-1)(x-2)\cdots(x-2009)) . .
Enfin, en développant H grâce aux formules de Viète, et en établissant l'égalité des coefficients de part et d'autres de la relation H(x)=xP(x)-1, on arrive à déterminer explicitement P.
On peut alors calculer P(0). Bien. Sauf que dans le dernier exercise, je ne vois pas comment tu peux arriver à P(0) avec cette methode (Je n'avais pas la chance de savoir les formules de viéte). | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 04 Nov 2010, 14:02 Jeu 04 Nov 2010, 14:02 | |
| - Dijkschneier a écrit:
- Solution au problème 19 :
On introduit le polynôme H(x)=xP(x) - 1 sur lequel on va travailler.
P est de degré 2008, H est donc de degré 2009.
De plus, H(1)=H(2)=...=H(2009)=0.
Mais alors, H peut s'écrire, selon le théorème de d'Alembert-Gauss, comme produit de polynômes du premier degré : H(x)=k(x-1)(x-2)...(x-2009).
De plus, d'après la définition de H, on a que H(0)=-1.
Donc : -1 = -k 2009!, donc  , où ! désigne la factorielle. , où ! désigne la factorielle.
Ainsi : %20=%20\frac{1}{2009!}(x-1)(x-2)\cdots(x-2009)) . .
Enfin, en développant H grâce aux formules de Viète, et en établissant l'égalité des coefficients de part et d'autres de la relation H(x)=xP(x)-1, on arrive à déterminer explicitement P.
On peut alors calculer P(0). J'ai fait le même passage, cependant je n'ai pas osé la poster, et voici les causes: Pour ce qui est en rouge: Même si on précise P explicitement, on aura un x au dénominateur. Donc en remplaçant par 0, le dénominateur s'annule et l'image ne peut jamais être calculée. Comment tu expliques cela? | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 04 Nov 2010, 17:35 Jeu 04 Nov 2010, 17:35 | |
| - nmo a écrit:
J'ai fait le même passage, cependant je n'ai pas osé la poster, et voici les causes:
Pour ce qui est en rouge: Même si on précise P explicitement, on aura un x au dénominateur.
Donc en remplaçant par 0, le dénominateur s'annule et l'image ne peut jamais être calculée.
Comment tu expliques cela? Si on range H par ordre décroissant de puissances, alors l'avant dernier coefficient de H serait d'après les formules de Viète :  . Ainsi, par identification de coefficients, on déduit que c'est aussi le dernier coefficient de P. Mais alors, P(0)=dernier coefficient de P=  . | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 05 Nov 2010, 12:30 Ven 05 Nov 2010, 12:30 | |
| - nmo a écrit:
- Problème 20:
- Dijkschneier a écrit:

Soient (D) et (Delta) deux droites parallèles du plan, et soient E et F deux points distincts des deux droites, et tels que E soit du côté de (D), et F de celui de (Delta). Trouver le ou les emplacements des deux points K et H de (D) et (Delta) respectivement qui minimisent la somme EK²+KH²+HF² et tels que (KH) soit perpendiculaire aux deux droites (D) et (Delta).
Bonne chance. Posons d=EK²+KH²+HF². On considère un repère cartésien orthonormé ) tel que l'axe des abcisses soit parallèle à (D) et l'axe des ordonnées est perpendiculaire à (D). Dans ce repère, on pose: ) , ) , ) , et ) . Puisque KH est constante, alors d est inférieure équivaut à dire que EK²+HF² est inférieure. Posons d'=EK²+HF². On a ^2+(c-0)^2})^2+(\sqrt{(a-x)^2+(d-b)^2})^2) . Donc ^2+(d-b)^2) . Donc ^2) . Soit en résumé ^2) . Pour simplifier, on pose ^2) . D'où +\alpha) . Donc +\alpha) . Donc ^2-\frac{a^2}{4})\big)+\alpha) . Donc ^2-\frac{a^2}{2}+\alpha) . Ainsi, d' est inférieure équivaut à ^2) inférieure, car  est constant. Donc ^2) est inférieur. (C'est à dire nul) Par conséquant  . Synthèse: On dessine (G) une droite parallèle à (D) et passant par E. Soit F' le projeté orthogonal de F sur G. On construit I le milieu de EF'. On construit ensuite H et K tel que I appartient à (HK). Sauf erreur. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 05 Nov 2010, 12:46 Ven 05 Nov 2010, 12:46 | |
| - Dijkschneier a écrit:
- Si on range H par ordre décroissant de puissances, alors l'avant dernier coefficient de H serait d'après les formules de Viète :
 . .
Ainsi, par identification de coefficients, on déduit que c'est aussi le dernier coefficient de P.
Mais alors, P(0)=dernier coefficient de P= . . Maintenant, je te comprends bien, si tu applique bien les formules de Viète. Car, personellement, j'ignore cela. Pour les autres exercices, c'est exellent, je les ai vérifié ligne par ligne et tout me semble correcte. Grosso modo, Bravo et bonne continuation. | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 05 Nov 2010, 13:47 Ven 05 Nov 2010, 13:47 | |
| Quelqu'un pour proposer dex exercices ? | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 05 Nov 2010, 20:59 Ven 05 Nov 2010, 20:59 | |
| Exercise 23:Resoudre en IR² le systéme suivant : 
Dernière édition par M.Marjani le Sam 06 Nov 2010, 11:48, édité 1 fois | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 05 Nov 2010, 23:29 Ven 05 Nov 2010, 23:29 | |
| @M.Marjani : si je compte bien, ton problème se doit d'être numéroté le problème 23. Et sa solution est triviale car cela ne consiste qu'à résoudre une équation du quatrième degré, et cela se fait de manière directe et déterministe. J'attends un problème 24 sans doute plus compétitif. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 06 Nov 2010, 02:08 Sam 06 Nov 2010, 02:08 | |
| - Dijkschneier a écrit:
- @M.Marjani : si je compte bien, ton problème se doit d'être numéroté le problème 23. Et sa solution est triviale car cela ne consiste qu'à résoudre une équation du quatrième degré, et cela se fait de manière directe et déterministe. J'attends un problème 24 sans doute plus compétitif.
Ok je vais l'edité. Mais le fait de remarquer que le systéme implique une équation de 4éme degré n'est qu'une goute d'eau sur une réviére (De mon avis) Sinon j'attend ta methode ou ton idée dans laquelle t'as résolu l'exercise façilement. Donc j'attend pour poster le 24 éme EX qui sera trés compétitif :d PS: C'est un exercise tiré d'un olympiade de 4éme phase du 1ér BAC : ) | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|   | | | | Préparations aux olympiades de première (2010-2011) |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
