| | Préparations aux olympiades du première (2011-2012) |  |
|
+6nmo boubou math Driss Ach Siba aymas Ahmed Taha (bis) 10 participants |
|
| Auteur | Message |
|---|
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Préparations aux olympiades du première (2011-2012) Sujet: Préparations aux olympiades du première (2011-2012)  Mar 07 Fév 2012, 22:37 Mar 07 Fév 2012, 22:37 | |
| salut a tous Je lance ce nouveau jeu pour bien se préparer aux olympiades de cette année (incha allah). les règles ils ont claire comme toujours : 1- chaque problème posté devrai avoir un numéro.
2- Les Solutions devrai être en spoiler .
3-Celui qui a trouvé la réponse, il doit poster un autre problème. Mais si la solution n'est pas trouvée pendant 3 jours, celui qui a posté le problème doit poster une réponse.
4- Si quelqu'un arrive à trouver une solution sans avoir un nouveau exercice qu'il indique pour que quelqu'un d'autre le fait .
5- De préférence les énoncés et les solutions devraient être rédigé en 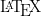
Enfin, je vous propose ces 12 exos : (c'est beaucoup mais facile) Problème 1:Calculer : ^2}}) Problème 2: Problème 2:Calculer :  Problème 3: Problème 3:Soit 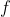 une fonction définie de 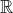 vers 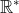 et vérifiant : =f(x-1).f(x+5)) Montrer que 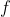 est périodique. Problème 4:Soit 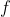 une fonction définie de 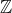 vers 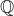 tel que : \&space;\&space;\&space;\&space;\&space;f(x+1)=\frac{1+f(x)}{1-f(x)}) sachant que =2) calculer ) . Problème 5: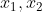 et 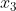 sont les solutions de l’équation : 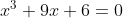 Sans calculer ces solution, déterminer la valeur de l’expression : 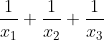 Problème 6: Problème 6: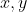 et  des réels strictement positifs . 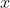 et 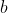 deux nombres relatifs Montrer que si 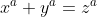 et 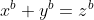 donc 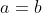 Problème 7: Problème 7: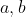 et  des réels strictement positifs. Montrer que : ) Problème 8: Problème 8: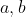 et  des réels strictement positifs. Montrer que : (a+c)}+\frac{b^2}{(a+b)(b+c)}+\frac{c^2}{(a+c)(b+c)}\geq&space;\frac{3}{4}) Problème 9: Problème 9:trouvé tous les nombres réels 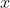 tel que : 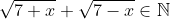 Problème 10: Problème 10:résoudre dans 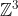 le système suivant : 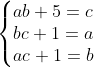 Problème 11: Problème 11:On considère un triangle ABC dont les mesures des côtés sont a, b et c tel que a est la plus grande. Démontrer que ABC est rectangle si et seulement si : \left&space;(\sqrt{a+c}+\sqrt{a-c}&space;\right&space;)=\sqrt{2}\left&space;(&space;a+b+c&space;\right&space;)) Problème 12: Problème 12:ABC un triangle S sont aire et P sont périmètre. Montrer que : 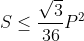 . | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 12:41 Mer 08 Fév 2012, 12:41 | |
| - Spoiler:
2 Pour le deuxième il s'agit d'une suite télescopique
il suffit de voir que 1/n(n+3)=1/3(1/n - 1/n+3)
ce qui facilite l'exo est le resultat est
S=1/3(1/2+1/3+1/4-1/2004-1/2005-1/2006) et a vous de calculer
Dernière édition par aymas le Mer 08 Fév 2012, 22:20, édité 1 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 12:47 Mer 08 Fév 2012, 12:47 | |
| - Spoiler:
3 pour le troisième
on a pour x=x+3
f(x+5)=f(x+2)f(x+8 )
alors f(x+8 )=f(x+5)/f(x+2)
=f(x-1)
donc f(x)=f(x+9)
c'est a dire f est périodique
Dernière édition par aymas le Mer 08 Fév 2012, 22:21, édité 2 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 12:56 Mer 08 Fév 2012, 12:56 | |
| - Spoiler:
4 pour le quatreime on a apres le calcul
f(x+2)=-1/f(x)
donc f(x+4)=-1/f(x+2)=f(X)
alors f est periodique de 4
et on a f(2006)=f(2+51*4)=f(2)=-3
Dernière édition par aymas le Mer 08 Fév 2012, 22:25, édité 1 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 13:00 Mer 08 Fév 2012, 13:00 | |
| - Spoiler:
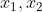 et 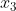 sont les solutions de l’équation alors x_1+x_2+x_3=0 x_1*x_2+x_1*x_3+x_2*x_3=9 x_1*x_2*x_3=6 alors 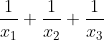 = (x_1*x_2+x_1*x_3+x_2*x_3)/(x_1*x_2*x_3)=3/2
Dernière édition par aymas le Mer 08 Fév 2012, 22:25, édité 1 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 13:45 Mer 08 Fév 2012, 13:45 | |
| - Spoiler:
pour le 7éme exercice d'apres IAG on a
sigma (a*(1/c² +1/b²))   superieur de 2*sigma(a/bc)
alors il suffit de prouver que
sigma(a/bc) est superieur de sigma(1/a)
qui est vrai puisqu 'il est équivalente a
a²+b²+c² est superieur de ab +ac +bc
qui laisse a conclure
 
Dernière édition par aymas le Mer 08 Fév 2012, 22:26, édité 1 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 13:49 Mer 08 Fév 2012, 13:49 | |
| - Spoiler:
pour l 8 eme exo
l'inégalité est équivalente à
a²b+a²c+b²c+b²a+c²a+c²b supérieur à 6abc
ce qui est vrai puisqu'il est équivalente à
a(b-c)²+b(a-c)²+c(b-a)² supérieur de 0
Dernière édition par aymas le Mer 08 Fév 2012, 22:26, édité 1 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 | |
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 14:27 Mer 08 Fév 2012, 14:27 | |
| salut a tous bravo aymas bon sol mais la prochaine fois veuillez respecter les règles du jeu - Citation :
- 1- chaque problème posté devrai avoir un numéro.
2- Les Solutions devrai être en spoiler .
3-Celui qui a trouvé la réponse, il doit poster un autre problème. Mais si la solution n'est pas trouvée pendant 3 jours, celui qui a posté le problème doit poster une réponse.
4- Si quelqu'un arrive à trouver une solution sans avoir un nouveau exercice qu'il indique pour que quelqu'un d'autre le fait .
5- De préférence les énoncés et les solutions devraient être rédigé en 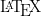
| |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 14:31 Mer 08 Fév 2012, 14:31 | |
| - Spoiler:
pour le 10eme exercice IL est clair que les solutions sont S=(3,-2,-1)(-2,3,-1)
Dernière édition par aymas le Mer 08 Fév 2012, 22:20, édité 3 fois | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 | |
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 14:32 Mer 08 Fév 2012, 14:32 | |
| je ne sait pas comment spoiler les reponses | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 14:36 Mer 08 Fév 2012, 14:36 | |
| - aymas a écrit:
- je ne sait pas comment spoiler les reponses
sélectionne les sol ------> Autre----->Spolier | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 14:36 Mer 08 Fév 2012, 14:36 | |
| oui je sais mais puisque le nombre doit etre entier et 14 est entier alors 49-x² doit etre un care parfait et puisque 49-x² est inférieur à 49 on peut conclure le resultat | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 14:38 Mer 08 Fév 2012, 14:38 | |
| | |
|
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 14:50 Mer 08 Fév 2012, 14:50 | |
| Salut, J'ai pas le temps de tout vous rédiger, mais je veux auqnd meme participer: Pour 1: S = 2013 - (1/3)^2009 Pour 4: f(2006) = -3 Pour 7: V(7+x) + V(7-x) appartient à {1,2,3,4,5,6,7}. Il reste plus qu'à résoudre les equations et faire les eliminations nécessaires pour trouver les solutions x. Pour 10: S = {(-2,3,-1);(3,-2,-1)} Pour le reste c'est en cours 
Dernière édition par Siba le Mer 08 Fév 2012, 17:20, édité 4 fois | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 15:05 Mer 08 Fév 2012, 15:05 | |
| | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 15:07 Mer 08 Fév 2012, 15:07 | |
| le réciproque est evidement clair | |
|
  | |
Driss Ach
Maître
 Nombre de messages : 117 Nombre de messages : 117
Age : 29
Date d'inscription : 29/10/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 15:11 Mer 08 Fév 2012, 15:11 | |
| quand même il faut donner la méthode et la résultat..et + respecter les règles de jeu pour n'a perd pas sa valeur  | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 15:21 Mer 08 Fév 2012, 15:21 | |
| - aymas a écrit:
- oui je sais mais puisque le nombre doit etre entier et 14 est entier alors 49-x² doit etre un care parfait et puisque 49-x² est inférieur à 49 on peut conclure le resultat
- aymas a écrit:
- existe ils des solutions
Oui il existe - Spoiler:
| |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 15:34 Mer 08 Fév 2012, 15:34 | |
| - Spoiler:
pour le premier 
| |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 15:41 Mer 08 Fév 2012, 15:41 | |
| abdelkrim-amine a ecrit
Oui il existe - Spoiler:
oui a methode conduit a ce resultat lorsque 49-x²=1 mais pense tu que  est un entier naturel
Dernière édition par aymas le Mer 08 Fév 2012, 15:48, édité 1 fois | |
|
  | |
Driss Ach
Maître
 Nombre de messages : 117 Nombre de messages : 117
Age : 29
Date d'inscription : 29/10/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 15:45 Mer 08 Fév 2012, 15:45 | |
| abdelkrime-amine à écrit: - Spoiler:
Problème 10:résoudre dans 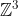 le système suivant : 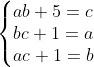
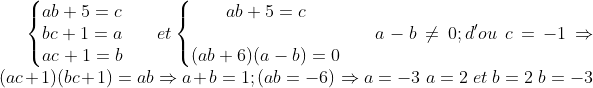 Alors 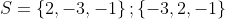 | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 | |
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 15:50 Mer 08 Fév 2012, 15:50 | |
| V48, ca donne 3.8 à peu près, et c'est pas un entier naturel ... | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  | |
| |
|
  | |
| | Préparations aux olympiades du première (2011-2012) |  |
|
