| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Préparations aux olympiades de première (2010-2011) Sujet: Préparations aux olympiades de première (2010-2011)  Mar 14 Sep 2010, 20:04 Mar 14 Sep 2010, 20:04 | |
| Comme l'évolution de l'âge est irrémédiable, et que le marathon consacré à la préparation des olympiades de seconde touche à sa fin, j'aimerais, en restant dans la même lancée, proposer d'entamer un nouveau marathon qui cette fois-ci sera conçu pour préparer les olympiades de première.
Un peu à la manière de tous les marathons, celui-ci aurait des règles qui ne sortent pas du commun :
- Dans l'idéal, chaque participant ayant donné une solution à un précédent problème doit se charger de proposer un nouveau problème. Si quelqu'un qui répond à un problème n'a pas de nouveau problème à proposer, qu'il l'indique clairement ! D'autres s'en chargeront, si possible.
- Numéroter clairement les problèmes, et citer le numéro du problème dans la solution que l'on en donne.
- Ne pas poster de solutions incomplètes et par conséquent, ne pas attendre de confirmation pour reproposer un nouveau problème.
- Favoriser l'entente et la bonne humeur.
Problème 1 :
Soient x, y et z des réels inférieurs ou égaux à 1 tels que x+y+z=1.
Montrer que 1/(1+x²) + 1/(1+y²) + 1/(1+z²) <= 27/10 | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 15 Sep 2010, 18:55 Mer 15 Sep 2010, 18:55 | |
| Solution du problème1:On a  . (1+z²)+1+x²+y²+x²y²}{(1+x²+y²+x²y²)(1+z²)}) . +3(x+y+z)+x²y²+y²z²+z²x²}{1+x²+y²+z²+x²y²+y²z²+z²x²+x²y²z²}) . +3(x+y+z)+x²y²+y²z²+z²x²}{1+x²+y²+z²+x²y²+y²z²+z²x²+x²y²z²} \le \frac{27}{10}) . Donc il suffit de démontrer que -10(2(z²+y²+x²)+3(x+y+z)+x²y²+y²z²+z²x²) \ge 0) . Et on a +17(x²z²+x²y²+y²z²)+27x²y²z²-3 \ge 0) .Ce qui est vrai. | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 15 Sep 2010, 19:06 Mer 15 Sep 2010, 19:06 | |
| Problème2:Déterminer toutes les fonctions 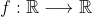 . telles que pour tous les réels x,y,z,t on a: +f(z))(f(y)+f(t))=f(xy-zt)+f(xt+yz)) . | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | |
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Sep 2010, 11:10 Ven 17 Sep 2010, 11:10 | |
| - Dijkschneier a écrit:
- louis a écrit:
Et on a +17(x²z²+x²y²+y²z²)+27x²y²z²-3 \ge 0) .Ce qui est vrai. .Ce qui est vrai. Pourquoi ? Voici une autre tentative: On a 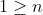 . 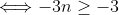 . 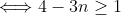 . Et ^2\ge0) . En multipliant, on trouve (1-3n)^2\ge0) . (1-6n+9n^2)\ge0) . 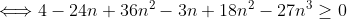 . 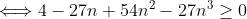 . 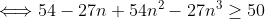 . \ge50) . 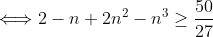 . (1+n^2)\ge\frac{50}{27}) . \ge\frac{1}{1+n^2}) . Remplaçons n par x, y et z successivement, on trouve que \ge\frac{1}{1+x^2}) . \ge\frac{1}{1+y^2}) . \ge\frac{1}{1+z^2}) . En sommant, on tombe sur +\frac{27}{50}(2-y)+\frac{27}{50}(2-z)\ge\frac{1}{1+x^2}+\frac{1}{1+y^2}+\frac{1}{1+z^2}) . \ge\frac{1}{1+x^2}+\frac{1}{1+y^2}+\frac{1}{1+z^2}) . )\ge\frac{1}{1+x^2}+\frac{1}{1+y^2}+\frac{1}{1+z^2}) . \ge\frac{1}{1+x^2}+\frac{1}{1+y^2}+\frac{1}{1+z^2}) . 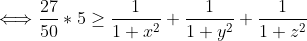 . 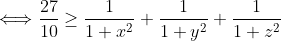 . Avec égalité si et seulement si 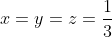 . | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Sep 2010, 11:57 Ven 17 Sep 2010, 11:57 | |
| | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Sep 2010, 16:27 Ven 17 Sep 2010, 16:27 | |
| Solution du problème 2:
Soit f une fonction réelle telle que pour tous réels x, y, z, t :
[f(x)+f(z)][f(y)+f(t)]=f(xy−zt)+f(xt+yz) (1)
a) Pour x=z et y=t= 0, il vient 4f(x)f(0)=2f(0), pour tout réel x. En particulier, 4[f(0)]²=2f(0). Et donc, f(0)=0 ou f(0)=1/2.
Si f(0)=1/2, la relation précédente conduit à f(x)=1/2, pour tout réel x.
Réciproquement, la fonction f: x->1/2 est bien solution du problème.
On suppose maintenant que f(0)=0.
b) Pour z=t=0, la relation (1) s'écrit: f(x)f(y)=f(xy) (2)
pour tous réels x, y. En particulier, pour tout réel x, on a f(x²) = [f(x)]².
Comme tout réel positif ou nul est un carré, cela assure que f est positive ou nulle sur R+.
c) Le membre de droite de la relation (1) est invariant par la transformation (x, y, z, t)->(z, x, y,−t).
Il doit donc en être de même du membre de gauche. Et donc, pour tous réels x, y, z, t: [f(x)+f(z)][f(y)+f(t)]=[f(z)+f(x)][f(y)+f(−t)].
Ou encore [f(x)+f(z)][f(t)−f(−t)]=0 (3)
Supposons que, pour tous réels x, z, on ait f(x)+f(z)=0. En particulier, pour x = z, il vient f(x) = 0.
Réciproquement, la fonction nulle est bien solution du problème.
On suppose maintenant que f n'est pas la fonction nulle. D'après ce qui précéde, il existe donc x, z de R, pour lesquels f(x)+f(z)#0. Mais alors, la relation (3) prouve que f(t)=f(−t), pour tout réel t, ce qui assure f est paire.
Notons qu'alors, d'après b), on a f>=0 sur R.
d) De (2), il vient f(x)=f(x)f(1), pour tout réel x. Et, comme f n'est pas la fonction nulle, c'est donc que f(1)=1. D'autre part, pour y=z=t=1, la relation (1) conduit à 2[f(x)+f(1)]=f(x−1)+f(x+1), pour tout réel x. Et ainsi f(x+1)=2f(x)+2−f(x−1).
Or, f(0)=0 et f(1)=1. Il est alors facile de vérifier par récurrence que f(x)=x², pour tout entier x>0. Et donc, par parité, on a f(x)=x², pour tout entier x.
Soient p, q deux entiers, avec q#0.
D'après (2), on a alors p²=f(p)=f(q)f(p/q)=q²f(p/q), d'où f(p/q)=p²/q², ce qui assure que f(x)=x², pour tout rationnel x.
e) Soient x, z des réels. Pour x=y et z=t, la relation (1) conduit à: [f(x)+f(z)]²=f(x²−z²)+f(2zx).
Pour x=y et z=−t, et en utilisant la parité de f, la relation (1) conduit à: [f(x)+f(z)]²=f(x²+z²).
Ainsi, f(x²+z²)=f(x²−z²)+f(2zx) (4) pour tous réels x, z.
Soient a, h de R+. En choisissant x, z de R+ tels que x=a+(h/2) et z²=h/2, on a a+h=x²+z² et a=x²−z². Et, d'après (4) et c), il vient alors f(a+h)−f(a)=f(2zx)>=0.
On en déduit que f est croissante sur R+.
f) Soit x de R+. On sait qu'il existe deux suites (r_n) et (r'_n) de rationnels positifs ou nuls telles que, pour tout n>=0, on ait r_n=<x<=r'_n, et lim (n->+00) r_n=lim (n->+00)r'_n=x.
Pour tout n>=0, puisque f est croissante et d'après les résultats du d), on a: r_n²=f(r_n)=<f(x)=<f(r'_n)=r'_n².
En faisant tendre n vers +00, il vient f(x)=x². Ainsi, f(x)=x² pour tout x de R+. Et par parité : f(x)=x² pour tout x de R.
Réciproquement, la fonction f: x->x² est bien solution du problème.
Finalement, les solutions du problème sont : f: x->x², f: x->1/2 et la fonction nulle. | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Sep 2010, 16:35 Ven 17 Sep 2010, 16:35 | |
| Problème 3:
Soit f une foction définie de N->N et qui satisfait les deux conditions suivantes:
1-f(f(x))=4n-3 pour tous entier n de N
2-f(2^n)=2^(n+1)-1 pour tous entier n de N
Calculez f(993) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Sep 2010, 18:00 Ven 17 Sep 2010, 18:00 | |
| - louis a écrit:
- Problème 3:
Soit f une foction définie de N->N et qui satisfait les deux conditions suivantes:
1-f(f(x))=4n-3 pour tous entier n de N
2-f(2^n)=2^(n+1)-1 pour tous entier n de N
Calculez f(993) Solution du problème 3:On a )=4n-3) .==>(*) En effectuant la transformation de  en 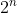 , la relation * s'écrit )=4*2^n-3) . Donc =2*2^{n+1}-2-1) . Donc =2(2^{n+1}-1)-1) . Et si on pose 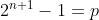 . On trouve que =2p-1) . Réciproquement, soit f la fonction définie de IN ver IN par =2p-1) . On a =2p-1) . Donc )=f(2p-1)) . Donc )=2(2p-1)-1) . Donc )=4p-2-1) . Donc )=4p-3) . Ainsi f vérifie la première condition. Et on a =2*2^n-1) . Donc =2^{n+1}-1) . Ainsi f vérifie la deuxième condition. On déduit que la fonction solution est =2p-1) . Pour n=993, on a =2*993-1) . Donc =1896-1) . Donc =1895) . Sauf erreur. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Sep 2010, 18:09 Ven 17 Sep 2010, 18:09 | |
| Je vous propose un exercice plus dur: Exercice 4:Résolvez en IR l'équation suivante:  . Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | |
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Sep 2010, 18:24 Ven 17 Sep 2010, 18:24 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Sep 2010, 20:47 Ven 17 Sep 2010, 20:47 | |
| - nmo a écrit:
Pourquoi? Je ne vois pas d'erreur. Car l'expression 2^(n+1) - 1 ne parcourt pas IN tout entier. | |
|
  | |
-Crash-
Habitué
 Nombre de messages : 22 Nombre de messages : 22
Age : 30
Date d'inscription : 24/02/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Sep 2010, 21:59 Ven 17 Sep 2010, 21:59 | |
| on a :
f(f(n))=4n-3 => f(4n-3)=4f(n)-3=>f(993)=4f(249)-3
on a :
f(2^(n+1)-1)=f(f(2^n))=2^(n+2)-3
avec la même méthode :
f(2^(n+2)-3)=2^(n+3)-7 et f(2^(n+3)-7)=2^(n+4)-15
pour n=5 on a : f(249)=483 => f(993)=1895 | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 18 Sep 2010, 12:31 Sam 18 Sep 2010, 12:31 | |
| - nmo a écrit:
- Je vous propose un exercice plus dur:
Exercice 4:
Résolvez en IR l'équation suivante:
 . .
Bonne chance. Merci d'expliciter les notations. La notation [.] réfère à quoi ? | |
|
  | |
chamitos007
Maître

 Nombre de messages : 163 Nombre de messages : 163
Age : 30
Date d'inscription : 27/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 18 Sep 2010, 16:50 Sam 18 Sep 2010, 16:50 | |
| wow vraiment .formidable la méthode de louis  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 20 Sep 2010, 14:27 Lun 20 Sep 2010, 14:27 | |
| - Dijkschneier a écrit:
- nmo a écrit:
Pourquoi? Je ne vois pas d'erreur. Car l'expression 2^(n+1) - 1 ne parcourt pas IN tout entier. Si, elle parcourt IN tout entièrement. Pour n=0, l'expression vaut 1. (0 est le petit entier). - Dijkschneier a écrit:
- nmo a écrit:
- Je vous propose un exercice plus dur:
Exercice 4:
Résolvez en IR l'équation suivante:
 . .
Bonne chance. Merci d'expliciter les notations.
La notation [.] réfère à quoi ? La notation [t] réfère à la fonction partie entière. N'essaie pas de le résoudre, il vaut mieux le changer par un autre. La solution que tu dois trouver en fin de ta solution est l'ensemble vide. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 20 Sep 2010, 14:43 Lun 20 Sep 2010, 14:43 | |
| Exercice 4:
On considère la fonction numérique g définie vers IR par g(g(g(x)))=x²-3x+4.
Calculez g(g(2)).
Bonne chance.
P.S: Je m'excuse pour l'exercice précédent. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 20 Sep 2010, 20:35 Lun 20 Sep 2010, 20:35 | |
| Si vous acceptez que je participe voiçi ma solution du probléme 4.. (J'ai résolu le premier exercise aussi l'autre fois) Solution 4:))=x^3-3x+4\textup{\textit{%20On%20veut%20calculer:%20}}g(g(2))) ------------------------------------------------------------------------------------------------------------------------------------ ))\geq%20x%20\textup{\textit{ Aussi:%20}}g(g(g(2)))=2) )=t\Rightarrow%20g(t)=2\Rightarrow%20g(g(2))=g(g(g(t)))=t^2-3t+4) ^2=0\Rightarrow t=2=g(g(2))) Merçi de signaler s'il y avait une error, je vois ça est court ^^ | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 20 Sep 2010, 22:21 Lun 20 Sep 2010, 22:21 | |
| bonsoir!!
C'est correct M.Marjani
juste pk tu as dit que IAG g(g(g(x)))>=x ça sert à quoi?? !!
A toi de poster ... | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 21 Sep 2010, 12:51 Mar 21 Sep 2010, 12:51 | |
| - Sporovitch a écrit:
- bonsoir!!
C'est correct M.Marjani
juste pk tu as dit que IAG g(g(g(x)))>=x ça sert à quoi?? !!
A toi de poster ... : O c'est bien donc dans 2 lignes. IAG qu'un indice pour vérifier à la fin, ou encore durant toutes les phases de la soluc :d C'est mieux de la supprimer pour consommer une ligne. Exercise 5:Trois nombres positifs x_1,x_2,x_3 satisfont aux conditions: x_1*x_2*x_3 > 1 Et x_1+x_2+x_3 < 1/x_1 + 1/x_2 + 1/x_3Montrer que: 1/ Aucun des trois nombres n'est égal à 1; 2/ L'un des trois nombres est plus petit que 1. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 21 Sep 2010, 22:04 Mar 21 Sep 2010, 22:04 | |
| Bonsoir tout le monde  juste une remarque Marjani, dans l'exercice précédent: g est-elle une bijection ?  Bonne continuation  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 22 Sep 2010, 01:49 Mer 22 Sep 2010, 01:49 | |
| - tarask a écrit:
- Bonsoir tout le monde

juste une remarque Marjani, dans l'exercice précédent: g est-elle une bijection ? 
Bonne continuation  @Tarask: Clà n'as pas de relation avec f est bijective.. : ) Je t'explique: *f(2) est une constante qui existe dans IR. Donc tu peux poser f(2)=t ou bien f(2)=c méme cas avec f(f(2)) .. : ) *Si tu veux dire c=t => f(c)=f(t) c'est une relation qui est toujours juste.. c'est plutot l'inverse qui a une relation avec l'injection. Bonne chançe : ) _________________ http://sphotos.ak.fbcdn.net/hphotos-ak-snc4/hs690.snc4/63083_132961873417884_100001122161029_160277_2925299_n.jpg | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 22 Sep 2010, 11:06 Mer 22 Sep 2010, 11:06 | |
| - nmo a écrit:
- Dijkschneier a écrit:
- nmo a écrit:
Pourquoi? Je ne vois pas d'erreur. Car l'expression 2^(n+1) - 1 ne parcourt pas IN tout entier. Si, elle parcourt IN tout entièrement.
Pour n=0, l'expression vaut 1.
(0 est le petit entier).
Parcourir IN veut dire prendre toutes les valeurs de IN, en d'autres termes, f(n) parcourt IN ssi f est surjective de IN vers IN. - M.Marjani a écrit:
Exercise 5:
Trois nombres positifs a,b et c satisfont aux conditions:
abc > 1 et a+b+c < 1/a + 1/b + 1/c
Montrer que:
1/ Aucun des trois nombres n'est égal à 1;
2/ L'un des trois nombres est plus petit que 1. Solution au problème 5 :1/ Supposons par l'absurde que l'un des nombres est égal à 1, mettons c. Alors la première condition devient : ab > 1, et la deuxième : a + b < 1/a + 1/b La deuxième est alors équivalente à 1 < 1/ab, ou encore à ab < 1. Contradiction avec le fait que ab > 1. 2/ Supposons par l'absurde que tous les nombres entre a, b et c sont supérieurs (strictement ?) à 1. Selon l'inégalité de Cauchy-Schwarz, on a a+b+c > 9/(1/a+1/b+1/c). Ainsi, la deuxième condition implique que 1/a + 1/b + 1/c > 3. Or 1/a, 1/b, 1/c < 1 car a,b et c > 1. De fait 1/a + 1/b + 1/c < 3. On a bien un discours contradictoire. PS : on peut supposer par l'absurde dans 2/ que les nombres sont strictement supérieurs à 1 sans perte de généralité car d'après 1/, aucun des nombres ne peut égaler 1. Et que chacun se sente libre de proposer un nouveau problème. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 22 Sep 2010, 11:30 Mer 22 Sep 2010, 11:30 | |
| - Dijkschneier a écrit:
- Solution au problème 5 :
1/ Supposons par l'absurde que l'un des nombres est égal à 1, mettons c.
Alors la première condition devient : ab > 1, et la deuxième : a + b < 1/a + 1/b
La deuxième est alors équivalente à 1 < 1/ab, ou encore à ab < 1.
Contradiction avec le fait que ab > 1.
2/ Supposons par l'absurde que tous les nombres entre a, b et c sont supérieurs (strictement ?) à 1.
Selon l'inégalité de Cauchy-Schwarz, on a a+b+c > 9/(1/a+1/b+1/c). Ainsi, la deuxième condition implique que 1/a + 1/b + 1/c > 3.
Or 1/a, 1/b, 1/c < 1 car a,b et c > 1. De fait 1/a + 1/b + 1/c < 3.
On a bien un discours contradictoire.
PS : on peut supposer par l'absurde dans 2/ que les nombres sont strictement supérieurs à 1 sans perte de généralité car d'après 1/, aucun des nombres ne peut égaler 1.
Et que chacun se sente libre de proposer un nouveau problème. Bonjour : ) Pour la premiére elle est juste. Pour la deuxiéme, tu n'as montré (peut-étre) qu'un cas parmi deux cas (Selon ma vision), il te faut discuter du cas oû seulement l'un des réels positives a,b,c est strictement positive à 1 : ) Une fois çelà est prouvé par l'absurde, il te reste un seule cas qui est deux réels positives parmi a,b,c sont strictement à 1. Ce que je le pense pas étre utile à déduire qu'un réel positive est plus petit que 1.. Pourtant je pense qu'il fallait chercher une autre methode, ou bien reprendre. Pour la methode que j'ai fais, la premiére question n'était qu'un complément de dire que tout est stricte : ) _________________ http://sphotos.ak.fbcdn.net/hphotos-ak-snc4/hs690.snc4/63083_132961873417884_100001122161029_160277_2925299_n.jpg
Dernière édition par M.Marjani le Mer 22 Sep 2010, 12:07, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
