|
| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants | |
| Auteur | Message |
|---|
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 20:47 Mer 16 Fév 2011, 20:47 | |
| Ce n'est pas suffisant.
Si on choisit deux éléments et qu'on applique l'opération plusieurs fois sur eux, alors évidemment, il n'y aura plus de changement à partir de la seconde application.
Mais alors, rien ne prévoit dans ta solution qu'on puisse appliquer l'opération sur d'autres éléments.
Par exemple :
4 12 16 7 18
Tu prends par exemple a=12 et b=18, ce qui donne, si on remplace a par le pgcd et b par le ppcm :
4 6 16 7 36
En appliquant l'opération sur 6 et 36 :
4 6 16 7 36
Donc il n'y a plus de changement.
Mais en l'appliquant sur 4 et 6 par exemple, il y a un changement !! | |
|   | | mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 20:51 Mer 16 Fév 2011, 20:51 | |
| - Dijkschneier a écrit:
- Ce n'est pas suffisant.
Si on choisit deux éléments et qu'on applique l'opération plusieurs fois sur eux, alors évidemment, il n'y aura plus de changement à partir de la seconde application.
Mais alors, rien ne prévoit dans ta solution qu'on puisse appliquer l'opération sur d'autres éléments.
Par exemple :
4 12 16 7 18
Tu prends par exemple a=12 et b=18, ce qui donne, si on remplace a par le pgcd et b par le ppcm :
4 6 16 7 36
En appliquant l'opération sur 6 et 36 :
4 6 16 7 36
Donc il n'y a plus de changement.
Mais en l'appliquant sur 4 et 6 par exemple, il y a un changement !! Oui, mais à un moment, il n'y a plus de changement. Quand on fait le même truc à tous les éléments. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 20:56 Mer 16 Fév 2011, 20:56 | |
| Non. Attention aux erreurs de conception.
Supposons qu'on ait 5 éléments : a1, a2, a3, a4, a5
Ce que tu fais est de prendre a1 et a2.
Tu appliques l'opération deux fois sur eux, et hop, il n'y a plus de changement. OK !
Tu prends a1 et a3.
Tu appliques l'opération deux fois sur eux, et hop, il n'y a plus de changement. OK !
etc.
Tu prends a1 et a5.
Tu appliques l'opération deux fois sur eux, et hop, il n'y a plus de changement. OK !
Maintenant, rebelote !
Tu prends a1 et a2.
Tu appliques l'opération deux fois sur eux, et hop, il n'y a plus de changement. OK !
etc.
Et on ne sait pas si on va finir ou pas !!
| |
|   | | mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 21:15 Mer 16 Fév 2011, 21:15 | |
| - Dijkschneier a écrit:
- Non. Attention aux erreurs de conception.
Supposons qu'on ait 5 éléments : a1, a2, a3, a4, a5
Ce que tu fais est de prendre a1 et a2.
Tu appliques l'opération deux fois sur eux, et hop, il n'y a plus de changement. OK !
Tu prends a1 et a3.
Tu appliques l'opération deux fois sur eux, et hop, il n'y a plus de changement. OK !
etc.
Tu prends a1 et a5.
Tu appliques l'opération deux fois sur eux, et hop, il n'y a plus de changement. OK !
Maintenant, rebelote !
Tu prends a1 et a2.
Tu appliques l'opération deux fois sur eux, et hop, il n'y a plus de changement. OK !
etc.
Et on ne sait pas si on va finir ou pas !!
Ah ouais ! Tu as raison. Je vais y réfléchir plus tard.  | |
|   | | darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 21:37 Mer 16 Fév 2011, 21:37 | |
| Bonsoir , pour le 64 : Remarquons d'abord que le PGCD de deux nombre divisent leurs PPCM , une simple écriture en sous forme de facteur premiers permet de le voir . Maintenant supposons qu'on est choisis deux nombres , il devient évident qu'a partir de la deuxième opération entre ces deux nombres rien ne changera . Posons A1 et A2 ces nombres : On a dans une case A1^A2 et dans l'autre PPCM(A1,A2) si on prend le PPCM et qu'on fait l'opération avec un troisième nombre A3 on a : =\prod&space;p_i^{MAX(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;)}=A4) Ce nombre est un multiple du PPCM(A1,A2) et de A3 il s'en suit qu'il est divisible par A1^A2 et donc qu'une opération faite entre ce nombre et le A1^A2 ne changerais rien . Maintenant dans l'autre case on aura : =\prod&space;p_i^{MIN(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;)}) Si on refait une opération entre ce nombre et A1^A2 : on aurait dans une case ce nombre : =\prod&space;p_i^{MIN(MIN(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;);PGCD(\alpha1,\alpha2))}) Ce nombre là divise tout les autres ( si PPCM(A1,A2)|A3) ce nombre serait égal à A1^A2 , dans le cas contraire , on aurait un nouveau nombre qui divise tout les autre et donc qui ne changera pas , de plus on a déjà vu que chacun des autre nombres divise A4 et que chaque pair prise donnera inévitablement Ai|Aj ; un dernier détail c'est l'autre case pour cette dernière opération qui contiendra : =\prod&space;p_i^{Max(Max(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;);PGCD(\alpha1,\alpha2))}=\prod&space;p_i^{Max(Max(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;)}=\prod&space;p_i^{(Max(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;)}=A4) Maintenant que le cas de trois nombres est fini on peut montré par simple récurrence que quelque soit le nombre de case dans le tableau après un certain nombre d'opération on aura des nombres tel que Ai|Aj et donc que rien ne changera après | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 17 Fév 2011, 12:34 Jeu 17 Fév 2011, 12:34 | |
| Solution au problème 66:
On a (x-1)(y-1)(z-1)>=0 d'parès les données donc :
2xyz-2xy-2xz2yz+2x+2y+2z-1>=0 on remplace par l'équation on trouve :
-(x+y+z)²+2(x+y+z)-1>=0 donc x+y+z=1 => (1)
ainsi x²+y²+z²+2xz+2yz+2xy=1, on remplace dans l'équation on trouve :
xy+yz+xz-xyz=0 ainsi (1-z)(xy+z)=0 ce qui donnne soit z=1 soit xy=-z
dans le deuxieme cas on a xy=x+y-1 soit (x-1)(y-1)=0 donc on a trois cas complétement similairess :
prenons par exemple le cas x=1 en remplacanat on trouve z=-y et en remplacant dans (1) on trouve z=y=0 et x=1
Ainsi les solution sont :
S={(1;0;0);(0;1;0);(0;0;1)}
CQFD | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 17 Fév 2011, 12:50 Jeu 17 Fév 2011, 12:50 | |
| - Mehdi.O a écrit:
- Solution au problème 66:
On a (x-1)(y-1)(z-1)>=0 d'parès les données donc :
2xyz-2xy-2xz2yz+2x+2y+2z-1>=0 on remplace par l'équation on trouve :
-(x+y+z)²+2(x+y+z)-1>=0 donc x+y+z=1 => (1)
ainsi x²+y²+z²+2xz+2yz+2xy=1, on remplace dans l'équation on trouve :
xy+yz+xz-xyz=0 ainsi (1-z)(xy+z)=0 ce qui donnne soit z=1 soit xy=-z
dans le deuxieme cas on a xy=x+y-1 soit (x-1)(y-1)=0 donc on a trois cas complétement similairess :
prenons par exemple le cas x=1 en remplacanat on trouve z=-y et en remplacant dans (1) on trouve z=y=0 et x=1
Ainsi les solution sont :
S={(1;0;0);(0;1;0);(0;0;1)}
CQFD Ce qui est en bleu n'est pas correcte, c'est plutot l'inverse: (x-1)(y-1)(z-1)=<0. | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 17 Fév 2011, 12:54 Jeu 17 Fév 2011, 12:54 | |
| - M.Marjani a écrit:
- Mehdi.O a écrit:
- Solution au problème 66:
On a (x-1)(y-1)(z-1)>=0 d'parès les données donc :
2xyz-2xy-2xz2yz+2x+2y+2z-1>=0 on remplace par l'équation on trouve :
-(x+y+z)²+2(x+y+z)-1>=0 donc x+y+z=1 => (1)
ainsi x²+y²+z²+2xz+2yz+2xy=1, on remplace dans l'équation on trouve :
xy+yz+xz-xyz=0 ainsi (1-z)(xy+z)=0 ce qui donnne soit z=1 soit xy=-z
dans le deuxieme cas on a xy=x+y-1 soit (x-1)(y-1)=0 donc on a trois cas complétement similairess :
prenons par exemple le cas x=1 en remplacanat on trouve z=-y et en remplacant dans (1) on trouve z=y=0 et x=1
Ainsi les solution sont :
S={(1;0;0);(0;1;0);(0;0;1)}
CQFD
Ce qui est en bleu n'est pas correcte, c'est plutot l'inverse: (x-1)(y-1)(z-1)=<0. Ah oui, merci je me suis un peu précipité , je vais rectifier  | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 17 Fév 2011, 19:32 Jeu 17 Fév 2011, 19:32 | |
| - darkpseudo a écrit:
- Bonsoir , pour le 64 :
Remarquons d'abord que le PGCD de deux nombre divisent leurs PPCM , une simple écriture en sous forme de facteur premiers permet de le voir .
Maintenant supposons qu'on est choisis deux nombres , il devient évident qu'a partir de la deuxième opération entre ces deux nombres rien ne changera .
Posons A1 et A2 ces nombres :
On a dans une case A1^A2 et dans l'autre PPCM(A1,A2) si on prend le PPCM et qu'on fait l'opération avec un troisième nombre A3 on a :
=\prod&space;p_i^{MAX(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;)}=A4)
Ce nombre est un multiple du PPCM(A1,A2) et de A3 il s'en suit qu'il est divisible par A1^A2 et donc qu'une opération faite entre ce nombre et le A1^A2 ne changerais rien . Maintenant dans l'autre case on aura :
=\prod&space;p_i^{MIN(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;)})
Si on refait une opération entre ce nombre et A1^A2 :
on aurait dans une case ce nombre :
=\prod&space;p_i^{MIN(MIN(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;);PGCD(\alpha1,\alpha2))})
Ce nombre là divise tout les autres ( si PPCM(A1,A2)|A3) ce nombre serait égal à A1^A2 , dans le cas contraire , on aurait un nouveau nombre qui divise tout les autre et donc qui ne changera pas , de plus on a déjà vu que chacun des autre nombres divise A4 et que chaque pair prise donnera inévitablement Ai|Aj ; un dernier détail c'est l'autre case pour cette dernière opération qui contiendra :
=\prod&space;p_i^{Max(Max(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;);PGCD(\alpha1,\alpha2))}=\prod&space;p_i^{Max(Max(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;)}=\prod&space;p_i^{(Max(PPCM&space;\&space;\alpha&space;1\alpha2&space;;&space;\alpha3&space;)}=A4)
Maintenant que le cas de trois nombres est fini on peut montré par simple récurrence que quelque soit le nombre de case dans le tableau après un certain nombre d'opération on aura des nombres tel que Ai|Aj et donc que rien ne changera après Oui, j'avais suivi à peu près la même approche en abordant le problème, et c'est ce que je m'attendais que vous exploitiez en l'ayant proposé à vous. L'idée fondamentale étant de prouver que "quelque soit le nombre de case dans le tableau après un certain nombre d'opération on aura des nombres tel que Ai|Aj et donc que rien ne changera après". Maintenant, il est vrai que ce n'es pas très formel comme solution, car même si tu dis qu'on peut généraliser par récurrence, il n'est pas évident de le faire à mon avis. | |
|   | | darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 17 Fév 2011, 20:25 Jeu 17 Fév 2011, 20:25 | |
| Je vous l'accorde , mais je pense que la même démarche peut être suivi à quelques modification près pour prouver l'hérédité . Je serais interessé par la solution du 66 ( l'équation est dans Q Je suppose ) , je cale dessus depuis un certain temps et puis personne ne la résolu , et merci d'avance . | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 17 Fév 2011, 20:59 Jeu 17 Fév 2011, 20:59 | |
| - Dijkschneier a écrit:
- Problème 66 : (** : deux étoiles)
Trouver tous les triplets (x,y,z) de [0,1]^3 tels que :
x²+y²+z²+2xyz=1. x,y,z ne sont pas à rechercher dans Q, mais dans l'intervalle [0,1]. Je vous laisse peut-être davantage de temps pour y réfléchir. | |
|   | | darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 17 Fév 2011, 21:51 Jeu 17 Fév 2011, 21:51 | |
| Bon voilà un essai , écrivons x,y,z sous la forme a1/b1;a2/b2,b3/b3 il est clair que a1 =< b1 de plus si a1=b1 les autres nombres serait égal à 0 et l'inégalité serait vérifié donc prenons a1<b1 a2<b2 a3<b3 ; aussi ces a1^b1=1 ( premiers entre eux ) et de même pour les autres l'inégalité ce réécri : +2a_1a_2a_3}{b_1b_2b_3}=1) par IAG on a : [img]http://latex.codecogs.com/gif.download?LHS&space;\geq&space;\frac&space;{4\sqrt[4]{2(a1a2a3^3b1b2b3)}}{b1b2b3}\Rightarrow&space;\frac{a_1a_2a_3}{b_1b_2b_3}\leq&space;\frac&space;{1}{8}[/img] Il suffit de faire une autre inégalitée pour l'autre partie , il ce fait tard donc je continu demain . Amicalement . | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 17 Fév 2011, 23:41 Jeu 17 Fév 2011, 23:41 | |
| - darkpseudo a écrit:
- Bon voilà un essai , écrivons x,y,z sous la forme a1/b1;a2/b2,b3/b3 il est clair que a1 =< b1
de plus si a1=b1 les autres nombres seraient égalent à 0 et l'inégalité serait vérifié donc prenons a1<b1 a2<b2 a3<b3 ; aussi ces a1^b1=1 ( premiers entre eux ) et de même pour les autres
l'équation se réécrit :
+2a_1a_2a_3}{b_1b_2b_3}=1)
Par IAG on a :
[img]http://latex.codecogs.com/gif.download?LHS&space;\geq&space;\frac&space;{4\sqrt[4]{2(a1a2a3^3b1b2b3)}}{b1b2b3}\Rightarrow&space;\frac{a_1a_2a_3}{b_1b_2b_3}\leq&space;\frac&space;{1}{8}[/img]
Il suffit de faire une autre inégalité pour l'autre partie , il ce fait tard donc je continurai demain . Amicalement . Oui, tu peux la supposer. Pourtant que si a_1=a_2 tu tombes alors au cas où x=1 donc y=-(z)=0. Jusque là, tout est juste. Il y a une petite faute dans: +2a_1a_2a_3}{b_1b_2b_3}={\color{green}%201}) Juste pour enlever l'ambiguïté, c'est plutôt [Cygma_{cyc}(a_1²b_2b_3)/b_1) + 2(a_1a_2a_3)]÷[b_1b_2b_3] Ainsi, l'utilisation de l'IAG ^3*b_1b_2b_3))^\frac{1}{4}}}{b_1b_2b_3}\Leftrightarrow%20xyz=\frac{a_1a_2a_3}{b_1b_2b_3}\leq\frac{1}{8}) semble à sa place. Je t'invite à réfléchir plus encore à ce beau exercice. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 18 Fév 2011, 12:41 Ven 18 Fév 2011, 12:41 | |
| - Mehdi.O a écrit:
- On a pour tout x_i c'est comme une E.F, on peut prendre des valeurs !!!
Bon j'ai pas utilisé Latex, ca serait nettement mieux!
La solution figure dans Dima dima si tu désires la voir  Mais de quelle DIMA DIMA tu parles, je dispose de la dernière édition et le problème que je propose n'y figure pas. - Citation :
- V(Sigma r_k²)=1 ainsi r_k=b.a_k.
Ainsi r_i=a_i/(V(Sigma a_k²) Ce n'est pas évident comme conclusion n'est-ce pas? Je recule un peu vers les questions trigonométriques proposé par M.Marjani l'autre fois: Le problème des sinus se résout en remarquant que: 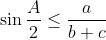 . Vous pouvez jeter un coup d'oeuil sur la solution dans un ancien topic de the kiler. Personnellement, j'ai oublié le lien et je ne suis même pas certain de la remarque que j'ai fait. Je vais proposer une solution alternative dans mes prochains messages. Au plaisir.
Dernière édition par nmo le Ven 18 Fév 2011, 13:33, édité 1 fois | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 18 Fév 2011, 13:02 Ven 18 Fév 2011, 13:02 | |
| - M.Marjani a écrit:
- Probléme 58: (**)
Prouver:
(i) 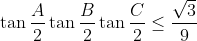 Je réponds: Il est aisé de vérifier que 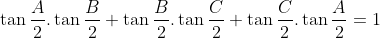 . D'un autre côté, on a A, B, et C sont les amplitudes des angles du triangle ABC, ils apprtiennent donc à l'intervalle ouvert 0,\pi\big() . Par conséquent, 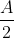 , 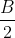 , et 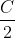 appartiennent bel et bien à l'intervalle ouvert 0,\frac{\pi}{2}\big() . Il vient donc que 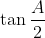 , 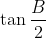 , et 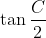 sont positifs. Maintenant, la version nouvelle de l'exercice est la suivante: Soient x, y, et z trois réels positifs tels que 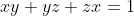 . Démontrez que 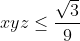 . On a selon l'inégalité arithmético-géométrique: ^{\frac{1}{3}}\le xy+yz+zx&\Leftrightarrow3.(x^2y^2z^2)^{\frac{1}{3}}\le1\\&\Leftrightarrow (xyz)^{\frac{2}{3}}\le \frac{1}{3}\\&\Leftrightarrow (xyz)^2\le \frac{1}{27}\\&\Leftrightarrow xyz\le \sqrt{{1}{27}}\end{align*}) . On remarque que 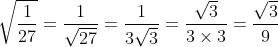 . Donc 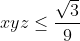 . CQFD. Sauf erreur.
Dernière édition par nmo le Ven 18 Fév 2011, 16:03, édité 1 fois | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 18 Fév 2011, 13:31 Ven 18 Fév 2011, 13:31 | |
| - M.Marjani a écrit:
- Probléme 58: (**)
Prouver:
(iii) 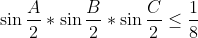 Je réponds encore une fois: Il est aisé de vérifier que 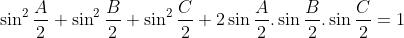 . D'un autre côté, on a A, B, et C sont les amplitudes des angles du triangle ABC, ils apprtiennent donc à l'intervalle ouvert 0,\pi\big() . Et puisque la fonction sinus est positive sur l'intervalle précédant, il vient que 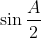 , 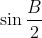 , et 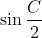 sont positifs. Maintenant, la version nouvelle de l'exercice est la suivante: Soient x, y, et z trois réels positifs tels que 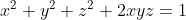 . Démontrez que 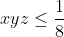 . On a selon l'inégalité arithmético-géométrique: ^{\frac{1}{3}}\le x^2+y^2+z^2&\Leftrightarrow 3(xyz)^{\frac{2}{3}}+2xyz\le x^2+y^2+z^2+2xyz\\&\Leftrightarrow 3(xyz)^{\frac{2}{3}}+2xyz\le1\\&\Leftrightarrow 2xyz+3(xyz)^{\frac{2}{3}}-1\le0\end{align*}) . On pose, en guise de simplification, 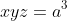 . La dernière ligne s'écrit ainsi: ^{\frac{2}{3}}+2a^3-1\le0) . Soit 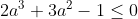 , et on remarqueque -1 est une solution évidente, on écrit donc: +3(a^2-1)\le0\\&\Leftrightarrow 2(a+1)(a^2-a+1)+3(a-1)(a+1)\le0\\&\Leftrightarrow (a+1)(2a^2-2a+2+3a-3)\le0\\&\Leftrightarrow (a+1)(2a^2+2a-a-1)\le0\\&\Leftrightarrow (a+1)(2a(a+1)-(a+1))\le0\\&\Leftrightarrow (a+1)(a+1)(2a-1)\le0\\&\Leftrightarrow (a+1)^2.(2a-1)\le0\\&\Leftrightarrow 2a-1\le0\\&\Leftrightarrow 2a\le1\\&\Leftrightarrow a\le\frac{1}{2}\\&\Leftrightarrow a^3\le\frac{1}{8}\end{align*}) . Et pour conclure, on écrit 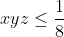 . CQFD. Sauf erreur. P.S: le résultat utilisé est déjà prouvé par yasserito, il ressemble aussi au problème récemment proposé.
Dernière édition par nmo le Ven 18 Fév 2011, 16:02, édité 1 fois | |
|   | | yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 18 Fév 2011, 14:11 Ven 18 Fév 2011, 14:11 | |
| c'est tres bien ce que vous avez fait. juste des petites remarques pour que les autres comprennent: pour ^{\frac{1}{3}}\le xy+y+zx&\Leftrightarrow3.(x^2y^2z^2)^{\frac{1}{3}}\le1\\&\Leftrightarrow (xyz)^{\frac{2}{3}}\le \frac{1}{3}\\&\Leftrightarrow (xyz)^2\le \frac{1}{27}\\&\Leftrightarrow xyz\le \sqrt{{1}{27}}\end{align*}) . vous avez oublie un z c'est plutot xy+yz+zx pas xy+y+zx! et pour Soit 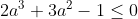 , et on remarqueque -1 est une solution évidente, on écrit donc: 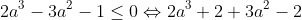 . c'est plutot 2a^3+3a^2-1 pas 2a^3-3a^2-1.juste des petites fautes d'inatention amicalement 
Dernière édition par yasserito le Sam 19 Fév 2011, 12:23, édité 2 fois | |
|   | | yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 18 Fév 2011, 14:15 Ven 18 Fév 2011, 14:15 | |
| veuillez svp rectifier . a vous de proposer un nouvel exercice!  | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 18 Fév 2011, 15:16 Ven 18 Fév 2011, 15:16 | |
| - yasserito a écrit:
- Pour le Probleme 58 de M.Marjani:
(ii)- Spoiler:
on a +sin^{2}(\frac{B}{2})+sin^{2}(\frac{C}{2})=\frac{1-cos(A)}{2}+\frac{1-cos(B)}{2}+\frac{1+cos(A+B)}{2}) et *sin(\frac{B}{2})*sin(\frac{C}{2})=(cos(\frac{A-B}{2})-cos(\frac{A+B}{2}))*cos(\frac{A+B}{2})) alors *sin(\frac{B}{2})*sin(\frac{C}{2})=\frac{cos(A)+cos(B)}{2}-\frac{cos(A+B)+1}{2}) finalement +sin^{2}(\frac{B}{2})+sin^{2}(\frac{C}{2})+2sin(\frac{A}{2})*sin(\frac{B}{2})*sin(\frac{C}{2})=1) C.Q.F.D sauf erreur 
Bien, c'est juste. - nmo a écrit:
- M.Marjani a écrit:
- Probléme 58: (**)
Prouver:
(i) 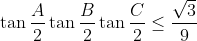 Je réponds:
- Spoiler:
Il est aisé de vérifier que 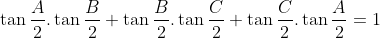 . D'un autre côté, on a A, B, et C sont les amplitudes des angles du triangle ABC, ils apprtiennent donc à l'intervalle ouvert 0,\pi\big() . Par conséquent, 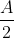 , 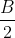 , et 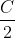 appartiennent bel et bien à l'intervalle ouvert 0,\frac{\pi}{2}\big() . Il vient donc que 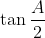 , 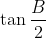 , et 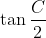 sont positifs. Maintenant, la version nouvelle de l'exercice est la suivante: Soient x, y, et z trois réels positifs tels que 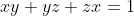 . Démontrez que 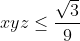 . On a selon l'inégalité arithmético-géométrique: ^{\frac{1}{3}}\le xy+y+zx&\Leftrightarrow3.(x^2y^2z^2)^{\frac{1}{3}}\le1\\&\Leftrightarrow (xyz)^{\frac{2}{3}}\le \frac{1}{3}\\&\Leftrightarrow (xyz)^2\le \frac{1}{27}\\&\Leftrightarrow xyz\le \sqrt{{1}{27}}\end{align*}) . On remarque que 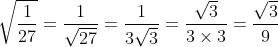 . Donc 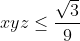 . CQFD. Sauf erreur.
- nmo a écrit:
- M.Marjani a écrit:
- Probléme 58: (**)
Prouver:
(iii) 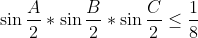 Je réponds encore une fois:
- Spoiler:
Il est aisé de vérifier que 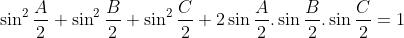 . D'un autre côté, on a A, B, et C sont les amplitudes des angles du triangle ABC, ils apprtiennent donc à l'intervalle ouvert 0,\pi\big() . Et puisque la fonction sinus est positive sur l'intervalle précédant, il vient que 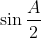 , 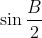 , et 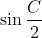 sont positifs. Maintenant, la version nouvelle de l'exercice est la suivante: Soient x, y, et z trois réels positifs tels que 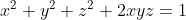 . Démontrez que 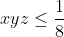 . On a selon l'inégalité arithmético-géométrique: ^{\frac{1}{3}}\le x^2+y^2+z^2&\Leftrightarrow 3(xyz)^{\frac{2}{3}}+2xyz\le x^2+y^2+z^2+2xyz\\&\Leftrightarrow 3(xyz)^{\frac{2}{3}}+2xyz\le1\\&\Leftrightarrow 2xyz+3(xyz)^{\frac{2}{3}}-1\le0\end{align*}) . On pose, en guise de simplification, 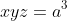 . La dernière ligne s'écrit ainsi: ^{\frac{2}{3}}+2a^3-1\le0) . Soit 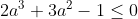 , et on remarqueque -1 est une solution évidente, on écrit donc: +3(a^2-1)\le0\\&\Leftrightarrow 2(a+1)(a^2-a+1)+3(a-1)(a+1)\le0\\&\Leftrightarrow (a+1)(2a^2-2a+2+3a-3)\le0\\&\Leftrightarrow (a+1)(2a^2+2a-a-1)\le0\\&\Leftrightarrow (a+1)(2a(a+1)-(a+1))\le0\\&\Leftrightarrow (a+1)(a+1)(2a-1)\le0\\&\Leftrightarrow (a+1)^2.(2a-1)\le0\\&\Leftrightarrow 2a-1\le0\\&\Leftrightarrow 2a\le1\\&\Leftrightarrow a\le\frac{1}{2}\\&\Leftrightarrow a^3\le\frac{1}{8}\end{align*}) . Et pour conclure, on écrit 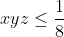 . CQFD. Sauf erreur.
P.S: le résultat utilisé est déjà prouvé par yasserito, il ressemble aussi au problème récemment proposé. C'est très bien. Les lemmes souhaités pour résoudre les 3 questions figurent au derniers exercices du manuel. P.S: Voir la partie: cours sur la trigonométrie. On peut dire que la question (iii) du problème 58, réponds au problème 66 proposé par Dijkschneier, après un changement de variables. . | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 18 Fév 2011, 15:40 Ven 18 Fév 2011, 15:40 | |
| - M.Marjani a écrit:
On peut dire que la question (iii) du problème 58, réponds au problème 66 proposé par Dijkschneier, après un changement de variables. Oui. Si tu rédiges une solution complète, ce serait à toi de proposer le nouveau problème. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 18 Fév 2011, 16:06 Ven 18 Fév 2011, 16:06 | |
| - yasserito a écrit:
- c'est tres bien ce que vous avez fait. juste des petites remarques pour que les autres comprennent:
pour http://latex.codecogs.com/gif.latex?\begin{align*}3.(xy.yz.zx)^{\frac{1}{3}}\le xy+y+zx&\Leftrightarrow3
vous avez oublie un z c'est plutot xy+yz+zx pas xy+y+zx!
et pour http://latex.codecogs.com/gif.latex?\begin{align*}2a^3-3a^2-1
c'est plutot 2a^3+3a^2-1 pas 2a^3-3a^2-1.juste des petites fautes d'inatention
amicalement  C'est rectifié. - yasserito a écrit:
- veuillez svp rectifier . a vous de proposer un nouvel exercice!
 Ce n'est pas à moi, j'ai justement donné un indice. Et je n'ai pas de problèmes à proposer. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 20 Fév 2011, 15:10 Dim 20 Fév 2011, 15:10 | |
| Puisque M.Marjani ne semble pas disposé à proposer une solution complète au problème 66, passons au problème 67. Je proposerais une solution au problème 66 dès que possible. Problème 67 : (** : deux étoiles)Soient E,F,G et H quatre ensembles, f une application de E vers F et g une application de G vers H. On considère l'application k de 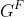 vers 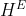 définie par : =g\circ%20u%20\circ%20f) où la notation 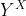 désigne l'ensemble des fonctions définies sur X et à valeurs dans Y. i) Montrer que si f est surjective et g est injective, alors k est injective ii) Montrer que si f est injective et g est surjective, alors k est surjective. Vous ne devez proposer une solution que si vous avez la réponse à i) et à ii) | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 20 Fév 2011, 15:25 Dim 20 Fév 2011, 15:25 | |
| Solution au problème 66 :Tentés par la forme de l'équation et par l'intervalle de définition des variables, nous pensons à utiliser une substitution trigonométrique. Posons alors : 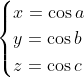 , où a et b et c appartiennent à [0,pi/2] Puisque a et b appartiennent à [0,pi/2], alors leur somme est inférieure à pi, et donc on peut définir c' = pi - a - b, de telle façon que a et b et c soient les angles d'un triangle. Mais alors, nous savons que : 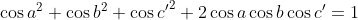 Et puisque l'on a aussi : x²+y²+z²+2xyz=1, alors 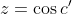 (on peut le déduire facilement) 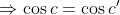 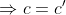 (car c et c' appartiennent à [0,pi/2] Par conséquent : 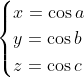 , où a et b et c appartiennent à [0,pi/2] et ont pour somme : pi. Inversement, des nombres ainsi définies sont solutions à l'équation. PS : on pouvait aussi s'en sortir, je crois, en utilisant la substitution trigonométrique qu'a préconisée M.Marjani
Dernière édition par Dijkschneier le Mer 23 Fév 2011, 22:02, édité 1 fois | |
|   | | yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 23 Fév 2011, 18:50 Mer 23 Fév 2011, 18:50 | |
| c'est x²+y²+z²+2xyz pas x+y+z+2xyz et la meme chose pour cos n'est ce pas ? amicalement  | |
|   | | yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 23 Fév 2011, 18:56 Mer 23 Fév 2011, 18:56 | |
| - Dijkschneier a écrit:
- Solution au problème 66 :
Mais alors, nous savons que : 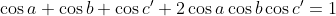
Et puisque l'on a aussi : x+y+z+2xyz=1, alors : }{1+2xy})
je crois que c'est cos²(a)+cos²(b)+cos²(c)+2cosacosbcosc qui egale 1 et la meme chose pour x+y+z+2xyz=1 c'est plutot x²+y²+z²+2xyz qui egale 1 selon votre enonce. la solution reste la meme la methode aussi,juste veuillez rectifier. amicalement:D | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|   | | | | Préparations aux olympiades de première (2010-2011) |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
