| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 23 Avr 2011, 16:49 Sam 23 Avr 2011, 16:49 | |
| Comme une lune d'une nuit obscure qui donne l'espoir aux gens si misérables, je vais jouer le rôle d'un héros qui doit sauver sa patrie: - amigo-6 a écrit:
- Bon jrepere lex 91 ou 81 ) -trouver tous les couples (a,b) d'entiers a supérieure ou égal à 1 et b supérieure ou égal à 1 vérifiant l'equation suivante:a^b^2=b^a
a^b^2 veu dire que a^b.b car b^2 = b.b Certes, l'exercice est très dur, cependant voici ma tentative: Je commence par le commencement: je dois démontrer quelques lemmes qui vont m'être utile à aboutir à la solution: Lemme 1:Soit a et b deux entiers. On a :(a^n)\wedge (b^n)=(a\wedge b)^n) . Voici la démonstration: Soit n un entier. On fait la décomposition de a et b en facteurs premiers: On a 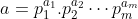 et 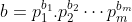 . Tels que 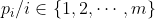 sont des entiers premiers. Donc 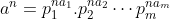 et 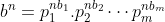 . Et tenon compte de la définition du plus grand commun diviseur, on écrit \wedge (b^n)=p_1^{\min\{na_1,nb_1\}}.p_2^{\min\{na_2,nb_2\}}\cdots p_m^{\min\{na_m,nb_m\}}) . Donc \wedge (b^n)=p_1^{n\min\{a_1,b_1\}}.p_2^{n\min\{a_2,b_2\}}\cdots p_m^{n\min\{a_m,b_m\}}) . Soit \wedge (b^n)=\bigg(p_1^{\min\{a_1,b_1\}}.p_2^{\min\{a_2,b_2\}}\cdots p_m^{\min\{a_m,b_m\}}\bigg)^n) . Et en vertu de 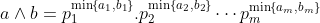 . Il s'ensuit que \wedge (b^n)=(a\wedge b)^n) . Il en résulte que :(a^n)\wedge (b^n)=(a\wedge b)^n) . Lemme 2:Soit a et b deux entiers. On a ^b\text{ est un entier}\Rightarrow \frac{a}{b}\text{ est un entier}) . Voici la démonstration: Démontrer l'implication en question revient à démontrer que ^b\text{ n'est pas un entier}) . Ou bien que \wedge (b^b)=1) . Supposons que 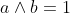 et démontrons que \wedge (b^n)=1) . On utilise le résultat déjà prouvé: :(a^n)\wedge (b^n)=(a\wedge b)^n) . Soit en posant n=b, \wedge (b^b)=1^b) car 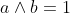 . Et ainsi \wedge (b^b)=1) . On vient de démontrer que \wedge (b^b)=1) . D'où ^b\text{ est un entier}\Rightarrow \frac{a}{b}\text{ est un entier}) . CQFD. Lemme 3:Soit p et n deux entiers naturels. Si p>1 et n>2, alors l'équation 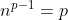 n'admet pas de solutions. Voici la démonstration: On a selon l'inégalité de Bernoulli, \in\mathbb{N}^*\times\mathbb{N}):(1+x)^y\ge 1+x.y) . Si on prend y=p-1 et x=n-1, il vient que: ^{p-1}\ge 1+(n-1)(p-1)&\Rightarrow n^{p-1}\ge 1+np-n-p+1\\&\Rightarrow p\ge np-n-p+2\\&\Rightarrow 2p-2+n-np\ge0\\&\Rightarrow 2(p-1)-n(p-1)\ge0\\&\Rightarrow (2-n)(p-1)\ge0\end{align*}) . La dernière préposition est fausse car: (2-n)\end{align*}) . Donc l'équation n'admet pas de solutions dans ce cas. Et ainsi: (\forall p>1):n^{p-1}>p) . Maintenant, je passe à la solution de l'exercice courant: On doit résoudre en 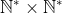 l'équation }=b^a) . On étudie pour cela deux cas, ou bien 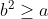 ou bien 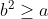 . Cas premier: 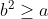 . On a donc 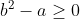 , ainsi 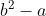 est un entier naturel. On a }=b^a) . Donc en divisant les deux côté de l'égalité par 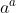 , on tombe sur }}{a^a}=\frac{b^a}{a^a}) . Soit ^a) .==>(*) Par définition 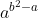 est un entier, ainsi ^a) l'est également. En utilisant le lemme 1, on trouve que  est un entier. C'est à dire qu'il existe un entier k, tel que 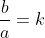 et ainsi 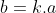 . En remplaçant dans *, il s'ensuit que ^2-a}=k^a) . Donc }=k^a) ou bien 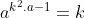 . Selon le lemme 3, on trouve d'un côté 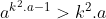 .==>(1) Et d'un autre, on a: 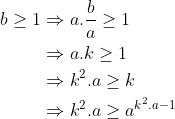 . Ce qui apporte contradiction à 1. Je viens donc de démontrer que si a>2, alors l'équation proposée n'admet pas de solution. Maintenant, si a=1; on a }=b^a) . Donc }=b^1) . C'est à dire 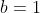 . Finalement, la seule solution possible dans ce cas est (1,1). Cas second:  . Je n'ai pas la solution dans ce cas et continuer à rechercher n'est qu'une grosse perte de temps. Je vais tricher en disant que l'exercice a omis la condition: 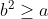 . J'attends vos remarques, ainsi que vos solutions si vous aboutissez à quelques choses. P.S: on peut aussi utiliser le résultat suivant: Soit a et b deux entiers, on a \in\mathbb{N}^2):(a^n)\wedge (b^p)=1) . Au lieu des deux premiers lemmes que j'ai utilisé.
Dernière édition par nmo le Sam 30 Avr 2011, 21:08, édité 6 fois (Raison : Terminer la rédaction de la solution) | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 23 Avr 2011, 18:42 Sam 23 Avr 2011, 18:42 | |
| Il est aussi grand temps que quelqu'un se charge de donner une solution à l'inégalité que Mehdi.O a préalablement proposé. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 23 Avr 2011, 19:08 Sam 23 Avr 2011, 19:08 | |
| - W.Elluizi a écrit:
- Il est aussi grand temps que quelqu'un se charge de donner une solution à l'inégalité que Mehdi.O a préalablement proposé.
J'avais résolu cette inégalité il y a longtemps, mais vu que personne ne semble vouloir poster une solution. Je m'en chargerais, et je posterais un nouvel exercice : Solution du problème 91:Nous nous devons de montrer que : ^{3}>&space;27(x^{2}y+y^{2}z+z^{2}x)) Vu la symétrie, on peut supposer que 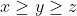 . ^{3}=4(\sum&space;x^{3}+3\sum&space;(x^{2}y+xy^{2})+6xyz)) . D'autre part par l'inégalité du réordonnement : 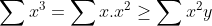 et cycliquement ... Aussi : \geq&space;\sum_{cyc}&space;(x^{2}y+xz^{2})=2\sum_{cyc}x^{2}y) En sommant ces résultats préliminaires, il en résulte que : ^{3}\geq&space;4(7\sum_{cyc}x^{2}y+6xyz)>&space;27\sum_{cyc}x^{2}y) CQFD. P.S: Notons que cette inégalité trop faible vu que la marge laissée est trop grande (  )... Problème 92:Trouvez toutes les fonctions  Tel que pour tous nombres réels strictement positifs a,b,c,d dont leur produit est égal à 1, nous avons : +f(b))(f(c)+f(d))=(a+b)(c+d)) | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 | |
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 23 Avr 2011, 20:11 Sam 23 Avr 2011, 20:11 | |
| - W.Elluizi a écrit:
- Mehdi.O a écrit:
Problème 92:
Trouvez toutes les fonctions 
Tel que pour tous nombres réels strictement positifs a,b,c,d dont leur produit est égal à 1, nous avons :
+f(b))(f(c)+f(d))=(a+b)(c+d)) - Spoiler:
Il est claire que f(1)=1
posons maintenant ab=1:
c'est à dire que 2(f(a)+f(b))=2(a+b)
et f(a)+f(b)+f(a)*f(b)=a+b+1
ce qui est équivaut au système suivant: f(a)*f(b)=1 et f(a)+f(b)=a+b
ce qui est équivalent à la résolution de l'équation suivante:X²-SX+P=0 tels que S=a+b et p=1
D'où il résulte que pour tout x strictement positif: f(x)=x qui est réciproquement une solution
Je pressens que la solution ci joint est un peu boiteuse,alors j'attends vos remarques.
Je ne comprends pas pourquoi ab=1=> f(a)*f(b)=1 ? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 23 Avr 2011, 20:17 Sam 23 Avr 2011, 20:17 | |
| C'est bon j'ai compris, ,en fait ta solution est un peu bourbeuse, mais en résolvant le système tu as oublié une solution, voilà nous avons soit f(a)=a ou f(a)=b d'autre part la condition donne b=1/a donc f(a)=a ou f(a)=1/a.
Mais stop, à ce stade nous avons montré que f(x)=x ou f(x)=1/x, en d'autre mots il se peut que les deux soient solutions en même temps. Donc supposons que il existe un p#1 tel f(p)=p et un q#1 tel que f(q)=1/q et pq=1... Ensuite en posant P(p;1;q,1): (p+1)(1/q+1)=(p+1)(q+1)=>(p+1)(1-q)(1+q)=0=> q=1 contradiction. Ce qui achève la preuve.
Synthèse: les deux solutions sont f(x)=1/x et f(x)=x
Vu que tu t'es approché de la solution, à toi l'honneur de poster un nouvel exercice.
Dernière édition par Mehdi.O le Sam 23 Avr 2011, 20:26, édité 1 fois | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 23 Avr 2011, 20:24 Sam 23 Avr 2011, 20:24 | |
| On a d'une part : +f(1))(f(b)+f(1))=(a+1)(b+1)\Rightarrow&space;f(a)*f(b)+f(a)+f(b)=ab+a+b=a+b+1) et d'autre part: )(f(a)+f(b))=2(a+b)\Rightarrow&space;f(a)+f(b)=a+b) ... | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 10:41 Dim 24 Avr 2011, 10:41 | |
| Problème 93: Soit  des réelles tels que:  Trouvez la valeur maximale de :  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 11:10 Dim 24 Avr 2011, 11:10 | |
| Solution au problème 93:- Spoiler:
Sans nuire à la généralité du problème on peut supposer que : 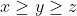 Ainsi par Chebsyev nous avons : (\sum&space;\frac{1}{x^{2}+1})) D'autre part la fonction  étant concave et en appliquant Jensen on trouve: ^{2}}{9}+1}) Ainsi: ^{2}}{9}+1}\leq&space;\frac{3}{2}\Leftrightarrow&space;((\sum&space;x)-3)^{2}\geq&space;0) Ce qui est vrai, ainsi la valeur maxiamale de cette expression est 3/2. Egalité si x=y=z=1
Dernière édition par Mehdi.O le Dim 24 Avr 2011, 14:12, édité 1 fois | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 13:10 Dim 24 Avr 2011, 13:10 | |
| - Mehdi.O a écrit:
- Solution au problème 93:
- Spoiler:
Sans nuire à la généralité du problème on peut supposer que : 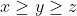 Ainsi par Chebsyev nous avons : (\sum&space;\frac{1}{x^{2}+1})) Aussi vu que Aussi vu que : ^{2}\geq&space;3(x+y+z)\Rightarrow&space;x+y+z\geq&space;3) D'autre part la fonction  étant concave et en appliquant Jensen on trouve: ^{2}}{9}+1}) Ainsi: ^{2}}{9}+1}\leq&space;\frac{3}{2}\Leftrightarrow&space;((\sum&space;x)-3)^{2}\geq&space;0) Ce qui est vrai, ainsi la valeur maxiamale de cette expression est 3/2. Egalité si x=y=z=1
Peux tu éclairer ma lanterne pour ce qui est du passage en rouge?!prendre:x=1/4 ;y=1/2;z=-5/2 | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 14:11 Dim 24 Avr 2011, 14:11 | |
| - W.Elluizi a écrit:
- Mehdi.O a écrit:
- Solution au problème 93:
- Spoiler:
Sans nuire à la généralité du problème on peut supposer que : 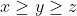 Ainsi par Chebsyev nous avons : (\sum&space;\frac{1}{x^{2}+1})) Aussi vu que Aussi vu que : ^{2}\geq&space;3(x+y+z)\Rightarrow&space;x+y+z\geq&space;3) D'autre part la fonction  étant concave et en appliquant Jensen on trouve: ^{2}}{9}+1}) Ainsi: ^{2}}{9}+1}\leq&space;\frac{3}{2}\Leftrightarrow&space;((\sum&space;x)-3)^{2}\geq&space;0) Ce qui est vrai, ainsi la valeur maxiamale de cette expression est 3/2. Egalité si x=y=z=1
Peux tu éclairer ma lanterne pour ce qui est du passage en rouge?!prendre:x=1/4 ;y=1/2;z=-5/2 x,y et z ne sont pas supposés être des réels positifs? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 14:13 Dim 24 Avr 2011, 14:13 | |
| Bon j'ai édité ma solution, elle est valable maintenant pour des réels tout court. On peut omettre le passage par I.A.G. | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 15:18 Dim 24 Avr 2011, 15:18 | |
| - Mehdi.O a écrit:
- Solution au problème 93:
- Spoiler:
Sans nuire à la généralité du problème on peut supposer que : 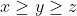 Ainsi par Chebsyev nous avons : (\sum&space;\frac{1}{x^{2}+1})) D'autre part la fonction  étant concave et en appliquant Jensen on trouve: ^{2}}{9}+1}) Ainsi: ^{2}}{9}+1}\leq&space;\frac{3}{2}\Leftrightarrow&space;((\sum&space;x)-3)^{2}\geq&space;0) Ce qui est vrai, ainsi la valeur maxiamale de cette expression est 3/2. Egalité si x=y=z=1
ُEn es tu sure?! De toutes les façons,c'est un problème sans trop d'intérêt,à toi maintenant d'en proposer un nouveau. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 15:20 Dim 24 Avr 2011, 15:20 | |
| - W.Elluizi a écrit:
- Mehdi.O a écrit:
- Solution au problème 93:
- Spoiler:
Sans nuire à la généralité du problème on peut supposer que : 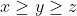 Ainsi par Chebsyev nous avons : (\sum&space;\frac{1}{x^{2}+1})) D'autre part la fonction  étant concave et en appliquant Jensen on trouve: ^{2}}{9}+1}) Ainsi: ^{2}}{9}+1}\leq&space;\frac{3}{2}\Leftrightarrow&space;((\sum&space;x)-3)^{2}\geq&space;0) Ce qui est vrai, ainsi la valeur maxiamale de cette expression est 3/2. Egalité si x=y=z=1
ُEn es tu sure?!
De toutes les façons,c'est un problème sans trop d'intérêt,à toi maintenant d'en proposer un nouveau. Traces la fonction et tu verras. Pour l'instant je n'ai pas de problèmes intéressants à proposer! | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 16:19 Dim 24 Avr 2011, 16:19 | |
| Problème 94:
Calculer la somme des nombres, qui peuvent petre composés par 6 nombres appartenant à l'ensemble {1,2,3,4,5,6} | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 17:12 Dim 24 Avr 2011, 17:12 | |
| - Mehdi.O a écrit:
- Problème 94:
Calculer la somme des nombres, qui peuvent petre composés par 6 nombres appartenant à l'ensemble {1,2,3,4,5,6} Bonjour ! le 1 reste comme chiffre d'unité 5! fois de meme pour le 2 , le 3 le , ... le 6 on somme donc les chiffres d'unité des nombres composés par {1;2;3;4;5;6) on trouve 5!+2.5!+3.5!+4.5!+5.5!+6.5!=A et puisqu'un nombre se formulant de 6 chiffre peut s'écrire ainsi (par exemple 123456 =1+2.10+3.100+4.1000+5.10000+6.100000) donc la somme des nombres qui peuvent etre compoosés par 6 nombres appartenant à l'ensemble {1;2;3;4;5;6} est : A+10A+100A+1000A+10000A+100000A=A(1+10+100+1000+10000+100000)=1111111A | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 17:15 Dim 24 Avr 2011, 17:15 | |
| - Sporovitch a écrit:
- Mehdi.O a écrit:
- Problème 94:
Calculer la somme des nombres, qui peuvent petre composés par 6 nombres appartenant à l'ensemble {1,2,3,4,5,6} Bonjour !
le 1 reste comme chiffre d'unité 5! fois de meme pour le 2 , le 3 le , ... le 6
on somme donc les chiffres d'unité des nombres composés par {1;2;3;4;5;6) on trouve 5!+2.5!+3.5!+4.5!+5.5!+6.5!=A
et puisqu'un nombre se formulant de 6 chiffre peut s'écrire ainsi (par exemple 123456 =1+2.10+3.100+4.1000+5.10000+6.100000) donc
la somme des nombres qui peuvent etre compoosés par 6 nombres appartenant à l'ensemble {1;2;3;4;5;6} est :
A+10A+100A+1000A+10000A+100000A=A(1+10+100+1000+10000+100000)=1111111A
Oui c'est la même procédure que j'ai établit. Juste une erreur de frappe dans le dernier résultat, c 111111 le 1 juste 6 fois  . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 17:16 Dim 24 Avr 2011, 17:16 | |
| - Mehdi.O a écrit:
- Problème 94:
Calculer la somme des nombres, qui peuvent petre composés par 6 nombres appartenant à l'ensemble {1,2,3,4,5,6} La réponse est 6*2211111. Si cela est vrai, je vais proposer ma démarche. Désolé, je n'ai pas vu le message qui contient la réponse de Sporovitch.
Dernière édition par nmo le Dim 24 Avr 2011, 19:22, édité 2 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 17:28 Dim 24 Avr 2011, 17:28 | |
| - nmo a écrit:
- Mehdi.O a écrit:
- Problème 94:
Calculer la somme des nombres, qui peuvent petre composés par 6 nombres appartenant à l'ensemble {1,2,3,4,5,6} La réponse est 6*2211111.
Si cela est vrai, je vais proposer ma démarche. Non, ta réponse est erronée : Voilà ma solution: Cette somme peut s'écrire de la sorte: 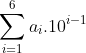 . Si on fixe un chiffre d'unités il se répètre 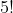 fois, puisque en arrageant les autres chiffres on obtient le résultat. De même pour les autres chiffres(dizaines,centaines ..) , donc il ne reste plus qu'à trier les cas, que chaque nombre de l'ensemble {1,2,3,4,5,6} est en quelle position dans le nombre : Ainsi la somme est égale à : (10^{5}+10^{4}+10^{3}+10^{2}+10^{1}+10^{0})=5!.21.\frac{10^{6}-1}{9}=279999720) | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 17:39 Dim 24 Avr 2011, 17:39 | |
| Problème 95 : (*) Résoudre dans IN :  où p est un nombre premier | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 18:23 Dim 24 Avr 2011, 18:23 | |
| - Sporovitch a écrit:
- Problème 95 : (*)
Résoudre dans IN :

où p est un nombre premier On va utiliser l'identité de Sophie Germain et puis résoudre. | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 18:41 Dim 24 Avr 2011, 18:41 | |
| Problème 96:a, b et c sont des réels positifs tels que abc=1. Prouver que: 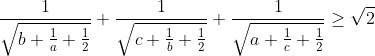 . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 19:20 Dim 24 Avr 2011, 19:20 | |
| - louis a écrit:
- Sporovitch a écrit:
- Problème 95 : (*)
Résoudre dans IN :

où p est un nombre premier On va utiliser l'identité de Sophie Germain et puis résoudre. Il faut détailler, sinon quel est l'intérêt de ce jeu? | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 | |
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Avr 2011, 22:28 Dim 24 Avr 2011, 22:28 | |
| - Sporovitch a écrit:
- Problème 95 : (*)
Résoudre dans IN :

où p est un nombre premier
a^4 + 4b^4 = p² <==> (a² + 2b²)² = p² + (2ab)² <==> (a² - 2ab + 2b²)(a² + 2ab + 2b²) = p² = p * p
Si p=/ 2 : Alors a²-2ab+2b² = p ET a²+2ab+2b² = p => 4ab=0. Si a=0 => p=2 et b=1. Si b=0 => p=a² Impossible.
Ou bien a²+2ab+2b² = p et a²-2ab + 2b² = 1 ==> (a-b)² + b² = 1 ==> a=b=1 ou a = b+1 et b=0 ou b = a+1 et b=0 Dans tous ces cas on trouve une contradiction .
Si p=2 : Alors a² + 2ab + 2b² = 4 et a² - 2ab + 2b² = 1 ==> 4 - 2ab = 1 + 2ab ==> 4ab = 3 Contradiction .
Et le cas d'égalité entre a²+2ab+2b² et a²-2ab+2b² est déjà établi ci-dessus .
Finalement, le seul triplet solution est quand p=2 , b=1 et a=0 . [Dans toute la démonstration, j'ai pris en considérence a²+2ab+2b² >= a²-2ab+2b²] Sauf erreur .
| |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
