| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 21 Mai 2011, 21:14 Sam 21 Mai 2011, 21:14 | |
| - expert_run a écrit:
- tu dois citer que n est un entier naturel car on parle de factoriel que pour les entiers naturels. Pour démontrer on utilisera le raisonnement par récurrence je vais essayé de la résoudre aujourd'hui.
Effectivement, n est censé être un entier naturel. C'est édité. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 21 Mai 2011, 22:18 Sam 21 Mai 2011, 22:18 | |
| - nmo a écrit:
- Je propose une inégalité faisant intervenir des entiers naturels:
Problème 102:
Soit n un entier naturel.
Démontrez que: ^{2n}\ge(4n)^n\times(n!)^3) . .
Bonne chance. S'il s'agit de la réccurence, tout devient clair. Surement qu'il existe une methode en se basant sur le binome de Newton + A{p}_{n} et C{p}{n} . Voici une solution: Pour n=0 : 0^0 >= 0^0 * 0 = 0 [Dévision par 0 est impossible] Donc doit normalement être n >= 1. Pour n=1 : 9 >= 4 juste. Supposons que ^{2n}=n^{2n}(n+2)^{2n}\geq (4n)^n*(n!)^3) et montrons que ^{2(n+1)}(n+3)^{2(n+1)}\geq 4(n+1)^{n+1}*((n+1)n!)^3) ^2(n+1)^{2n}(n+3)^{2(n+1)}\geq 4(n+1)^n*(n!)^3(n+1)^4) ^n(n+3)^{2(n+1)}\geq 4(n!)^3(n+1)^2) Il suffira de Montrer que )^n*(n+3)^{2n}\geq (4n)^n(n!)^3\textup{\mathrm{ Car }}(n+3)^2\geq (n+1)^2) Ou encore il suffira de Montrer que: )^n*(n+3)^{2n}\geq n^{2n}(n+2)^{2n}) Qui est largement juste puisqu'elle est équivalente à: ^n(n+3)^{2n}\geq (n)^n(n+2)^{2n}) Car: ^{2n}\geq (n+2)^{2n}\textup{\mathrm{ et }}(n+1)^n\geq n^n)
Dernière édition par M.Marjani le Sam 21 Mai 2011, 23:10, édité 2 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 21 Mai 2011, 22:41 Sam 21 Mai 2011, 22:41 | |
| Dans ton raisonnement il y a une faille je crois dans la dernière équivalence. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 21 Mai 2011, 22:48 Sam 21 Mai 2011, 22:48 | |
| - expert_run a écrit:
- Dans ton raisonnement il y a une faille je crois dans la dernière équivalence.
Une erreur de frappe oui . C'est édité. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 21 Mai 2011, 23:03 Sam 21 Mai 2011, 23:03 | |
| dans la ligne ou t a fait une implication ça se voit qu'il y a une faute. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 21 Mai 2011, 23:15 Sam 21 Mai 2011, 23:15 | |
| - expert_run a écrit:
- dans la ligne ou t a fait une implication ça se voit qu'il y a une faute.
Laquelle ? Je ne vois pas l'erreur si on s'est lance à demontrer une inégalité plus forte que son origine. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 21 Mai 2011, 23:22 Sam 21 Mai 2011, 23:22 | |
| non regarde bien quand ta dis car (n+3)^2 > (n+3)^2 ta dévisé son faire attention qu' avec inverse c est le contraire | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 21 Mai 2011, 23:43 Sam 21 Mai 2011, 23:43 | |
| @Expert_run: Monsieur, tout ce que j'ai essayé de montrer c'est: ^n(n+3)^{2(n+1)}{\color{Magenta} (*)}\geq (n+1)^n(n+3)^{2n}*(n+1)^2){\color{DarkRed} (**)}\geq 4(n!)^3(n+1)^2{\color{DarkGreen} (T)}) On a bien (*) >= (**) car (n+3)^2 >= (n+1)^2 , donc si (**) >= (T) alors forcément (*) >= (T) . Tu vois ? :d - nmo a écrit:
- darkpseudo a écrit:
- PROBLEME 101 :
Résoudre dans Q^3 :
x^3+2y^3+4z^3=6xyz Je réponds, même si je ne suis pas certains de ma solution:
Je vais me sevir de l'identité remarquable: \bigg((a-b)^2+(b-c)^2+(c-a)^2\bigg)) . .
Si on a  . .
Alors \bigg((a-b)^2+(b-c)^2+(c-a)^2\bigg)=0) . .
Et par conséquent, ou bien ^2+(b-c)^2+(c-a)^2=0) , ou bien , ou bien 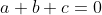 . .
Le deuxième cas est facile, on considère donc le cas où ^2+(b-c)^2+(c-a)^2=0) . .
Donc ^2=0) , , ^2=0) , et , et ^2=0) . .
Ainsi 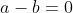 , , 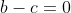 , et , et 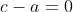 . .
Soit 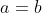 , , 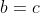 , et , et 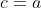 . .
Et finalement 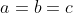 . .
Je reviens à notre problème:
On prends 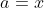 , ,  , et , et  . .
Ainsi l'équation proposée entraine ou bien  ou bien ou bien  . .
Cas premier:  . .
Si y est différent de 0, alors  . .
Ce qui est absurde, car  . .
Il en résulte que y=0, et par conséquent x=z=0.
Cas second:  . .
Je démontre d'abord l'équivalence suivante: :r.k\in\mathbb{Q}\Leftrightarrow k=0) . .
Soit r un nombre irrationnel:
-Supposons que  , et démontrons que k=0. , et démontrons que k=0.
On a  . .
Il existe donc un nombre rationnel q tel que 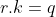 . .
Supposons par l'absurde que k est différent de zéro.
Ainsi  . .
Et par conséquent r est un nombre rationnel, ce qui est absurde.
On en conclut que k=0.
-L'autre implication est tout à fait triviale.
Il en résulte que :r.k\in\mathbb{Q}\Leftrightarrow k=0) . .
On a  . .
Donc  . .
Soit ) . . On est d'accord jusque cette étape. Mais tu dois précisé l'ensemble ou se trouve le k. - nmo a écrit:
- On sait d'ores et déjà que
) est un nombre rationnel. est un nombre rationnel.
Et selon l'équivalence que je viens de démontrer, il vient que  . .
Soit  . .
Si z est différent de zéro, on aura une contradiction pareille à la première.
Donc z=0, et cela conduit à y=0.
Il s'ensuit que x=0 lui aussi.
Réciproquement le triplet ) satisfait l'équation proposée. satisfait l'équation proposée.
Conclusion:
L'équation adment donc une solution unique qui n'est autre que le triplet ) . .
Sauf erreur. Non cela on le connait pas. Une fois k est irrationnel la démonstration que t'as inclu perd sa véracité. Dans ce cas t'as le nombre y - 2^{1/3}z irrationnel donc je comprends de cela que t'as pris k irrationnel. Contre exemple: k = m/r et m dans IQ verifie bien rk = q sans k =0. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 22 Mai 2011, 18:05 Dim 22 Mai 2011, 18:05 | |
| - M.Marjani a écrit:
- nmo a écrit:
- On sait d'ores et déjà que
) est un nombre rationnel. est un nombre rationnel. Non cela on le connait pas. Une fois k est irrationnel la démonstration que t'as inclu perd sa véracité.
Dans ce cas t'as le nombre y - 2^{1/3}z irrationnel donc je comprends de cela que t'as pris k irrationnel.
Contre exemple: k = m/r et m dans IQ verifie bien rk = q sans k =0. On le connait, car x est rationel et ) . L'équivalence que j'ai démontré, équivaut à dire: Soit r un nombre irrationnel. On a r.k est un nombre rationnel si et seulement si k=0. J'espère que tu me comprends maintenant. Pour l'autre exercice, j'avais commis une faute de frappe: il n'y a pas de 2, c'est simplement n(n+1). Je suis vraiment désolé. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 22 Mai 2011, 19:14 Dim 22 Mai 2011, 19:14 | |
| Ok pas grave on va refaire | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 22 Mai 2011, 21:29 Dim 22 Mai 2011, 21:29 | |
| - expert_run a écrit:
- tu dois citer que n est un entier naturel car on parle de factoriel que pour les entiers naturels. Pour démontrer on utilisera le raisonnement par récurrence je vais essayé de la résoudre aujourd'hui.
Qui a dit ça ?  http://fr.wikipedia.org/wiki/Fonction_Gamma_d%27Euler | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 22 Mai 2011, 21:44 Dim 22 Mai 2011, 21:44 | |
| XD ya que toi pour trouver des trucs aussi tordu chers imo-iste  ( j'esper que tu vas bien ) ... | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 22 Mai 2011, 21:46 Dim 22 Mai 2011, 21:46 | |
| - mizmaz a écrit:
- expert_run a écrit:
- tu dois citer que n est un entier naturel car on parle de factoriel que pour les entiers naturels. Pour démontrer on utilisera le raisonnement par récurrence je vais essayé de la résoudre aujourd'hui.
Qui a dit ça ? 
http://fr.wikipedia.org/wiki/Fonction_Gamma_d%27Euler Je crois que ta pas bien compris cette fonction n reste toujours un entier naturel mais seulement z qui appartient a c | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 22 Mai 2011, 22:17 Dim 22 Mai 2011, 22:17 | |
| XD Elhansi je commence a douté de ton intégrité morale , n'empêche je préfère quand t'est pas sérieux  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 24 Mai 2011, 20:07 Mar 24 Mai 2011, 20:07 | |
| @Darkpseudo: - Spoiler:
Ouee la chaleur fait mal ..!
- nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
- On sait d'ores et déjà que
) est un nombre rationnel. est un nombre rationnel. Non cela on le connait pas. Une fois k est irrationnel la démonstration que t'as inclu perd sa véracité.
Dans ce cas t'as le nombre y - 2^{1/3}z irrationnel donc je comprends de cela que t'as pris k irrationnel.
Contre exemple: k = m/r et m dans IQ verifie bien rk = q sans k =0. On le connait, car x est rationel et ) . .
L'équivalence que j'ai démontré, équivaut à dire: Soit r un nombre irrationnel.
On a r.k est un nombre rationnel si et seulement si k=0.
J'espère que tu me comprends maintenant.
Pour l'autre exercice, j'avais commis une faute de frappe: il n'y a pas de 2, c'est simplement n(n+1).
Je suis vraiment désolé. Je parle plutôt de la démonstration de l'équivalence. Si tu vois bien le contre exemple que j'ai presenté tu vas en conclure sa fausté. On ne peut pas passer à ce qui est en rouge. - nmo a écrit:
- darkpseudo a écrit:
- PROBLEME 101 :
Résoudre dans Q^3 :
x^3+2y^3+4z^3=6xyz Je réponds, même si je ne suis pas certains de ma solution:
Je vais me sevir de l'identité remarquable: \bigg((a-b)^2+(b-c)^2+(c-a)^2\bigg)) . .
Si on a  . .
Alors \bigg((a-b)^2+(b-c)^2+(c-a)^2\bigg)=0) . .
Et par conséquent, ou bien ^2+(b-c)^2+(c-a)^2=0) , ou bien , ou bien 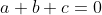 . .
Le deuxième cas est facile, on considère donc le cas où ^2+(b-c)^2+(c-a)^2=0) . .
Donc ^2=0) , , ^2=0) , et , et ^2=0) . .
Ainsi 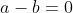 , , 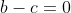 , et , et 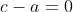 . .
Soit 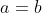 , , 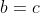 , et , et 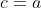 . .
Et finalement 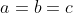 . .
Je reviens à notre problème:
On prends 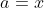 , ,  , et , et  . .
Ainsi l'équation proposée entraine ou bien  ou bien ou bien  . .
Cas premier:  . .
Si y est différent de 0, alors  . .
Ce qui est absurde, car  . .
Il en résulte que y=0, et par conséquent x=z=0.
Cas second:  . .
Je démontre d'abord l'équivalence suivante: :r.k\in\mathbb{Q}\Leftrightarrow k=0) . .
Soit r un nombre irrationnel:
-Supposons que  , et démontrons que k=0. , et démontrons que k=0.
On a  . .
Il existe daonc un nombre rationnel q tel que 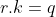 . .
Supposons par l'absurde que k est différent de zéro.
Ainsi  . .
Et par conséquent r est un nombre rationnel, ce qui est absurde.On en conclut que k=0.
-L'autre implication est tout à fait triviale.
Il en résulte que :r.k\in\mathbb{Q}\Leftrightarrow k=0) . .
On a  . .
Donc  . .
Soit ) . .
On sait d'ores et déjà que ) est un nombre rationnel. est un nombre rationnel.
Et selon l'équivalence que je viens de démontrer, il vient que  . .
Soit  . .
Si z est différent de zéro, on aura une contradiction pareille à la première.
Donc z=0, et cela conduit à y=0.
Il s'ensuit que x=0 lui aussi.
Réciproquement le triplet ) satisfait l'équation proposée. satisfait l'équation proposée.
Conclusion:
L'équation adment donc une solution unique qui n'est autre que le triplet ) . .
Sauf erreur. Et je ne comprends pas pourquoi ce qui est en rouge est juste . "K" est-il un rationel pour dire cela ? Je ne pense pas que ce passage soit juste, par exemple si q=3 et k=V(3) tu auras r=V(3) irrationel. Et pour l'équivalence tu prends par contre exemple: r=V2 et k=V(2) , rk=2 £ Q mais k est différent de 0. | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 25 Mai 2011, 14:26 Mer 25 Mai 2011, 14:26 | |
| - nmo a écrit:
Je démontre d'abord l'équivalence suivante: :r.k\in\mathbb{Q}\Leftrightarrow k=0) . .
Soit r un nombre irrationnel:
-Supposons que  , et démontrons que k=0. , et démontrons que k=0.
On a  . .
Il existe daonc un nombre rationnel q tel que 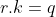 . .
Supposons par l'absurde que k est différent de zéro.
Ainsi  . .
Et par conséquent r est un nombre rationnel, ce qui est absurde.
On en conclut que k=0.
-L'autre implication est tout à fait triviale.
Il en résulte que :r.k\in\mathbb{Q}\Leftrightarrow k=0) . .
On a  . .
Donc  . .
Soit ) . .
On sait d'ores et déjà que ) est un nombre rationnel. est un nombre rationnel.
Et selon l'équivalence que je viens de démontrer, il vient que  . .
Soit  . .
Si z est différent de zéro, on aura une contradiction pareille à la première.
Donc z=0, et cela conduit à y=0.
Il s'ensuit que x=0 lui aussi.
Réciproquement le triplet ) satisfait l'équation proposée. satisfait l'équation proposée.
Conclusion:
L'équation adment donc une solution unique qui n'est autre que le triplet ) . .
Sauf erreur. Cette équivalence est juste si K appartient à Q. Donc, il fallait préciser l'ensemble auquel appartient K, car si K est irrationnel, on peut simplement prendre r= √3, k=√3 et on a r.k=3 c'est à dire il appartient bel et bien à Q et pourtant k≠0. - M.Marjani a écrit:
- nmo a écrit:
- On sait d'ores et déjà que
) est un nombre rationnel. est un nombre rationnel.
Et selon l'équivalence que je viens de démontrer, il vient que  . .
Soit  . .
Si z est différent de zéro, on aura une contradiction pareille à la première.
Donc z=0, et cela conduit à y=0.
Il s'ensuit que x=0 lui aussi.
Réciproquement le triplet ) satisfait l'équation proposée. satisfait l'équation proposée.
Conclusion:
L'équation adment donc une solution unique qui n'est autre que le triplet ) . .
Sauf erreur.
Non cela on le connait pas. Une fois k est irrationnel la démonstration que t'as inclu perd sa véracité.
Dans ce cas t'as le nombre y - 2^{1/3}z irrationnel donc je comprends de cela que t'as pris k irrationnel.
Contre exemple: k = m/r et m dans IQ verifie bien rk = q sans k =0. Donc, puisque nous résolvons l'équation dans Q, on cherche les solutions dans Q, par conséquent on considère k de Q. on a  si on sait que ça appartient à Q avec y et z de Q. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 26 Mai 2011, 13:05 Jeu 26 Mai 2011, 13:05 | |
| Vous faites tout un sujet d'un exo qui peut être résolu en trois lignes avec la descente infini, vous devriez passé à autre chose . | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 26 Mai 2011, 14:24 Jeu 26 Mai 2011, 14:24 | |
| Problème 103:Soit la fonction 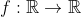 qui vérifie: \; f(x+y^{2n+1})=f(x)+(f(y))^{2n+1} \quad \forall x,y \in \mathbb{R} \text{ et } \forall n \in \mathbb{N} ) 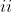\; f'(0) \ge 0) Trouvez l'expression de )
Dernière édition par louis le Jeu 26 Mai 2011, 20:37, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 26 Mai 2011, 14:48 Jeu 26 Mai 2011, 14:48 | |
| - darkpseudo a écrit:
- Vous faites tout un sujet d'un exo qui peut être résolu en trois lignes avec la descente infini, vous devriez passé à autre chose .
Merci de proposer une solution, car je ne sais pas comment procéder. - louis a écrit:
- Problème 102:
Soit la fonction 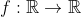 qui vérifie: qui vérifie:
\; f(x+y^{2n+1})=f(x)+(f(y))^{2n+1} \quad \forall x,y \in \mathbb{R} \text{ et } \forall n \in \mathbb{N} )
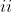\; f'(0) \ge 0)
Trouvez l'expression de ) Quelle anarchie! Deux exercices sans solutions et tu proposes un troisième. Merci de bien lire les règles du marathon. Même si tu propose un exercice, sache que 102+1=103. Ton problème, si tu ne l'enlève pas, doit être renuméroté. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 26 Mai 2011, 16:52 Jeu 26 Mai 2011, 16:52 | |
| Pour ta question nmo , on peut ce rammener à une étude sur Z en posant x=a/d y=b/d et z=c/d , Ensuite des divisions successives par 2 donnes la contradiction . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 26 Mai 2011, 21:12 Jeu 26 Mai 2011, 21:12 | |
| - darkpseudo a écrit:
- Pour ta question nmo , on peut ce rammener à une étude sur Z en posant x=a/d y=b/d et z=c/d , Ensuite des divisions successives par 2 donnes la contradiction .
Je n'ai jamais pensé à une telle solution. Merci bien. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 26 Mai 2011, 22:42 Jeu 26 Mai 2011, 22:42 | |
| Mais de rien mon cher .
Solution du 103 :
Je n'ai pas compris à quoi sert la deuxième hypothèse ,et je pense qu'il manque la continuité ?! | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 26 Mai 2011, 22:45 Jeu 26 Mai 2011, 22:45 | |
| - nmo a écrit:
- darkpseudo a écrit:
- Pour ta question nmo , on peut ce rammener à une étude sur Z en posant x=a/d y=b/d et z=c/d , Ensuite des divisions successives par 2 donnes la contradiction .
Je n'ai jamais pensé à une telle solution.
Merci bien. Mais cela n'empêche que ce que tu as suivi comme méthode dans ta solution procède d'une idée intéressante quand même...  | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 28 Mai 2011, 11:26 Sam 28 Mai 2011, 11:26 | |
| - darkpseudo a écrit:
- Je n'ai pas compris à quoi sert la deuxième hypothèse ,et je pense qu'il manque la continuité ?!
Elle sert à bien saisir l'expression et pour la continuité aussi de la deuxième. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 28 Mai 2011, 12:59 Sam 28 Mai 2011, 12:59 | |
| Je parlais de continuité sur R pas en 0 . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
