| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
Mehdi.A
Maître
 Nombre de messages : 100 Nombre de messages : 100
Age : 60
Date d'inscription : 07/05/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 20:19 Ven 10 Juin 2011, 20:19 | |
| - M.Marjani a écrit:
- @Mehdi.O: Quand tu fixe b sur 0 tu transgresses le fait que a,b sont premiers entre eux. Cela implique b|a premiérement.
- Spoiler:
- Mehdi.A a écrit:
- Moi aussi je ne sais pas pourquoi tu insiste sur ce mot la puisque tu l'a favorisé à d'autre plus simple ! en tous cas je crois que je dois m'excuser .. je ne savais pas que " si c'était" est ta nouvelle lemme .. enfin tu favorise toujours tes lemme non ? :p
De ce jour tu dois faire attention à ton ortographe, oui, mais c'est évident pour gagner une étoile de plus.. !!
Oui Oui bien sur !! Mais il y a une très grande différence entre " tes lemme" et ..... Montrer que si c'étaient a, b des entiers positives et relativement premiers entre eux, Alors qu'il existe deux entiers m et n tel qu'il soit a^m + b^n 1 (mod ab). C'est faux même en le prononçant ..  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 20:31 Ven 10 Juin 2011, 20:31 | |
| - M.Marjani a écrit:
- @Mehdi.O: Quand tu fixes b sur 0 tu transgresses le fait que a,b sont premiers entre eux. Cela implique b|a premiérement.
De la présence du b=0 et declarer qu'il existe une faute dans le probléme j'ai pensé vitement à b=0 ou a=0. Le probléme serait donc toujours juste en fixant m, n. - Spoiler:
- Mehdi.A a écrit:
- Moi aussi je ne sais pas pourquoi tu insiste sur ce mot la puisque tu l'a favorisé à d'autre plus simple ! en tous cas je crois que je dois m'excuser .. je ne savais pas que " si c'était" est ta nouvelle lemme .. enfin tu favorise toujours tes lemme non ? :p
- M.Marjani a écrit:
- De ce jour tu dois faire attention à ton ortographe, oui, mais c'est évident pour gagner une étoile de plus.. !!
- Mehdi.A a écrit:
- Oui Oui bien sur !! Mais il y a une très grande différence entre " tes lemme" et .....
Montrer que si c'étaient a, b des entiers positives et relativement premiers entre eux,
Alors qu'il existe deux entiers m et n tel qu'il soit a^m + b^n 1 (mod ab).
C'est faux même en le prononçant ..  On espére que si c'était juste une telle faute du pluriel xD (la phrase dans son bon emploie) J'ai juste collé l'exercice moi et tel qu'il l'est mon cher :d t'inquiétes pas quand méme :p
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 29 Juin 2011, 19:30 Mer 29 Juin 2011, 19:30 | |
| - M.Marjani a écrit:
- Probléme 105:
Montrer que si c'étaient a, b des entiers positives et relativement premiers entre eux,
Alors qu'il existe deux entiers m et n tel qu'il soit a^m + b^n  1 (mod ab). 1 (mod ab). Est ce que cela veut dire que a appartient à l'ensemble des nombres premiers, ainsi que b? Ou bien que le plus grand diviseurs commun à a et b est bel et bien 1? J'attends une réponse. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 30 Juin 2011, 03:51 Jeu 30 Juin 2011, 03:51 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Probléme 105:
Montrer que si c'étaient a, b des entiers positives et relativement premiers entre eux,
Alors qu'il existe deux entiers m et n tel qu'il soit a^m + b^n  1 (mod ab). 1 (mod ab). Est ce que cela veut dire que a appartient à l'ensemble des nombres premiers, ainsi que b?
Ou bien que le plus grand diviseurs commun à a et b est bel et bien 1?
J'attends une réponse. Non pas necessairement des nombres premiers, mais plutôt a^b=1. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 01 Juil 2011, 19:34 Ven 01 Juil 2011, 19:34 | |
| - M.Marjani a écrit:
- Probléme 105:
Montrer que si c'étaient a, b des entiers positives et relativement premiers entre eux,
Alors qu'il existe deux entiers m et n tel qu'il soit a^m + b^n  1 (mod ab). 1 (mod ab). Le problème est dur, je ne vais pas proposer une solution mais je vais étudier un cas. Après, je vais donner l'idée du travail, que je n'ai pas pu démontrer. Soit a et b deux nombres premiers, démontrons que ) . On a selon le petit théorème de fermat ) , puisque b est premier. Et de même ) , puisque a est premier. On a donc  et  . Ce qui implique que .\big(b^{a-1}-1\big)) . Ou bien  . Et comme  , car  et  . (Cela est valable car  et  puisque  et  ). Il s'ensuit que  , soit  . On peut donc écrire ) . CQFD. En analysant cette démonstration, je peux affirmer que pour arriver à résoudre le problème 105 on doit démontrer que :a^m\equiv1(b)) et que :b^n\equiv1(a)) . Là bas, je me bloque parfaitement. Je demande à M.Marjani de proposer une solution pour qu'on puisse avancer dans le jeu. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 02 Juil 2011, 02:13 Sam 02 Juil 2011, 02:13 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Probléme 105:
Montrer que si c'étaient a, b des entiers positives et relativement premiers entre eux,
Alors qu'il existe deux entiers m et n tel qu'il soit a^m + b^n  1 (mod ab). 1 (mod ab). Le problème est dur, je ne vais pas proposer une solution mais je vais étudier un cas.
Après, je vais donner l'idée du travail, que je n'ai pas pu démontrer.
Soit a et b deux nombres premiers, démontrons que ) . .
On a selon le petit théorème de fermat ) , puisque b est premier. , puisque b est premier.
Et de même ) , puisque a est premier. , puisque a est premier.
On a donc  et et  . .
Ce qui implique que .\big(b^{a-1}-1\big)) . .
Ou bien  . .
Et comme  , car , car  et et  . .
(Cela est valable car  et et  puisque puisque  et et  ). ).
Il s'ensuit que  , soit , soit  . .
On peut donc écrire ) . .
CQFD.
En analysant cette démonstration, je peux affirmer que pour arriver à résoudre le problème 105 on doit démontrer que :a^m\equiv1(b)) et que et que :b^n\equiv1(a)) . Là bas, je me bloque parfaitement. . Là bas, je me bloque parfaitement.
Je demande à M.Marjani de proposer une solution pour qu'on puisse avancer dans le jeu. Tu as fait le cas ou a,b sont premiers. Il fallait utiliser le theoréme trés connu d'Euler sur les nombres, qui est une généralisation du PTF (qui ne traite que le cas où n est un nombre premier) et est lui-même généralisé par le théorème de Carmichaël (à conaitre par coeur). Ainsi la relation que tu cherches nmo est trouvé et bien réalisé: l'existence du n et du m est garanti par l'indicatrice d'Euler Phi, c-à-d le n=φ(a) et le m=φ(b) . Je ne dispose d'aucun bon exercice pour le moment, je laisse la main. | |
|
  | |
n.naoufal
Expert sup

 Nombre de messages : 595 Nombre de messages : 595
Age : 33
Localisation : France.
Date d'inscription : 05/11/2008
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 02 Juil 2011, 10:50 Sam 02 Juil 2011, 10:50 | |
| Je me permets de poser cet exercice:
P.S: c'est édité.
Dernière édition par n.naoufal le Sam 02 Juil 2011, 13:30, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 02 Juil 2011, 13:18 Sam 02 Juil 2011, 13:18 | |
| @n.naoufal: Le triplet a=2, b=0, x=1 répond bien à l'énoncé, la question non plus. Peut-être a,b sont non nuls ? | |
|
  | |
n.naoufal
Expert sup

 Nombre de messages : 595 Nombre de messages : 595
Age : 33
Localisation : France.
Date d'inscription : 05/11/2008
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 02 Juil 2011, 13:29 Sam 02 Juil 2011, 13:29 | |
| Je dirai oui, car sinon on aura à l'aide de a=2,b=0 les solutions 2 et 1 dont le 1 est un carré parfait.
| |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 02 Juil 2011, 14:51 Sam 02 Juil 2011, 14:51 | |
| Solution au probléme 106:
On a x^2-(a^2-a+1)(x-b^2-1)-(b^2+1)^2 = 0
<==> (x-b²-1)(x²+b²+1-a²+a-1) = 0
<==> x=b²-1 ou x²+b²-a²+a=0
Si x=b²-1: Et x se différe de 0 alors PGCD(b²-1, b²)=1 , x ne sera plus un carré parfait.
Si x=0, on aura à l'aide de l'équation du départ a²=a donc a=1 et a>b => b=0. contradiction.
Si x²+b²-a²+a=0:
L'équation x²-(a²-a+1)(x-b²-1)-(b²+1)^2=0 <==> x²=(a²-a)(x-b²-1)+x
D'ou (a²-a)(x-b²-1)+x=a²-a-b² <==> (a²-a)(b²+2-x)=b²+x
Maintenant, on a x²+b²-a²+a=0 et comme résultat (a²-a)(b²+2-x)=b²+x. Alors a²-a=(a²-a)(b²+2-x) ==> b²+2-x=1 d'ou x=b²+1 qui est bel est bien une contradiction avec x carré parfait.
CQFD. | |
|
  | |
n.naoufal
Expert sup

 Nombre de messages : 595 Nombre de messages : 595
Age : 33
Localisation : France.
Date d'inscription : 05/11/2008
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 02 Juil 2011, 17:11 Sam 02 Juil 2011, 17:11 | |
|
Il y a des erreurs de calcul, mais sinon ça marche, pour montrer que
a^2-a-b^2 n'est pas carré Il suffit que:
a^2-a-b^2=p^2 alors (2a-1+2b)(2a+1-2b)=(2p)^2+1. Et (2a-1+2b) et (2a-1-2b) sont de la forme 4k+3 ainsi il existe c premier de la forme 4k+3 tq c|(2m)^2+1 alors Contradition!
| |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 03 Juil 2011, 00:28 Dim 03 Juil 2011, 00:28 | |
| Oui n.naoufal, en effet je l'ai pas remarqué, j'ai passé trés vite qu'avec des calculs mentales.
J'aime ta solution, mais il y a une trés simple pour s'en sortir:
a²-a-b²=0 <==> a(a-1)=b² qui n'est juste que si a=1 , et de a>b on tire b=0 qui est une contradiction.
L'implication se démontre facilement.. je l'ai déjà prouvé quelque part dans le forum.
Dernière édition par M.Marjani le Lun 04 Juil 2011, 13:15, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 03 Juil 2011, 19:22 Dim 03 Juil 2011, 19:22 | |
| Puisque c'est mon tour de proposer, je vous propose ces deux exercices: Problème 107:Soit 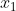 , 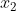 , ... et 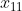 11 nombres rééls. Parmi ces rééls, montrez qu'il existe deux distincts 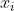 et 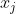 tel que ^2\le\bigg(1-\frac{2}{\sqrt{5}}\bigg)(1+x_i.x_j)^2) . Problème 108:Démontrez qu'il existe une infinité de nombres premiers de la forme 4n+3. Bonne chance.
Dernière édition par nmo le Lun 04 Juil 2011, 12:09, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 03 Juil 2011, 22:42 Dim 03 Juil 2011, 22:42 | |
| | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 03 Juil 2011, 23:51 Dim 03 Juil 2011, 23:51 | |
| Solution au problème 108 :- Spoiler:
Supposons par l'absurde qu'il existe qu'un nombre fini de nombres premiers qui sont congru à 3 modulo 4. Ainsi , \in&space;\mathbb{N}^k:\forall&space;i\in&space;\left&space;\{&space;1,2,..,k\left.&space;\right&space;\}&space;\right.:p_i\equiv&space;3(mod4)) . Sans nuire à la généralité du problème on peut supposer que :  Maintenant deux cas se présente devant nous : - Cas 1 :  . Ainsi on pose : ) Ce qui assure une contradiction vu que  est premier. En effet si il existe un :p_l\mid&space;N\Rightarrow&space;p_l\mid&space;N-\prod_{i=1}^{k}p_i=2) alors cela est absude ! - Cas 2 :  . On pose : \equiv&space;3(mod4)) ce qui assure de nouveau une contradiciton vu que  est premier, et en suivant le même raisonnement on trouve que :  Ce qui est absurde ! Ainsi il existe une infinité de nombres de premiers congru à 3 modulo 4.
P.S: j'attends toujours une réponse de la part de nmo pour le problème 108.
Dernière édition par Mehdi.O le Dim 03 Juil 2011, 23:58, édité 2 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 03 Juil 2011, 23:54 Dim 03 Juil 2011, 23:54 | |
| Il est mieux que tu postes un exercice en attendant le réponse de NMO. | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 03 Juil 2011, 23:57 Dim 03 Juil 2011, 23:57 | |
| @Mehdi.O : Il y'a quand même de petites subtilités pour affirmer que N est premier. tu peux le rédiger stp ? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 03 Juil 2011, 23:59 Dim 03 Juil 2011, 23:59 | |
| - Othmaann a écrit:
- @Mehdi.O : Il y'a quand même de petites subtilités pour affirmer que N est premier. tu peux le rédiger stp ?
C'est évident non ? | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 04 Juil 2011, 00:03 Lun 04 Juil 2011, 00:03 | |
| Les pi sont uniquement les premiers qui sont congru à 3 mod 4. je pense qu'il est trivial d'assurer que N n'est pas divisible par les pi , qu'en est il des autres premiers ? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 04 Juil 2011, 12:07 Lun 04 Juil 2011, 12:07 | |
| - Mehdi.O a écrit:
- Pour le problème 107 c t_i ou bien x_i ?
et i et j sont-ils distincts ? Ce sont des x. Pour i et j, ils sont distincts. Le problème est maintenant édité. Ta solution pour le problème 108 est bonne. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Juil 2011, 18:23 Sam 09 Juil 2011, 18:23 | |
| Je vais faire une solution pour le problème 107 plus tard, et je vous propose maintenant ces deux problèmes: Problème 109:Calculez }) . Problème 110:Soit ABCD un quadrilatère cyclonique, et soit (C) son cercle circonscrit. Soient I, J, K et L les milieux respectifs des arcs [AB], [BC], [CD] et [DA] du cercle (C). Démontrez que les droites (IK) et (JL) sont perpendiculaires. P.S: 107 et 109 font partie de la liste des nombres premiers jumeaux. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Juil 2011, 18:55 Sam 09 Juil 2011, 18:55 | |
| - nmo a écrit:
- Je vais faire une solution pour le problème 107 plus tard, et je vous propose maintenant ces deux problèmes:
Problème 109:
Calculez }) . .
Problème 110:
Soit ABCD un quadrilatère cyclonique, et soit (C) son cercle circonscrit.
Soient I, J, K et L les milieux respectifs des arcs [AB], [BC], [CD] et [DA] du cercle (C).
Démontrez que les droites (IK) et (JL) sont perpendiculaires.
P.S: 107 et 109 font partie de la liste des nombres premiers jumeaux. C'est quoi un quadrilatère cyclonique ? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Juil 2011, 19:02 Sam 09 Juil 2011, 19:02 | |
| Solution au problème 110:
Soit E l'intersection de (IK) et (JL):
Nous avons , angle{IEJ}=1/2(arc(IJ)+arc(LK))=1/2(arc(IB)+arc(BJ)+arc(DK)+arc(DL))=1/4(arc(AB)+arc(BC)+arc(DC)+arc(AD))=1/4.360=90.
CQFD. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Juil 2011, 19:03 Sam 09 Juil 2011, 19:03 | |
| Le problème 109 est classique, ce serait mieux de le changer. | |
|
  | |
mtb
Féru
 Nombre de messages : 30 Nombre de messages : 30
Age : 29
Date d'inscription : 28/06/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Juil 2011, 19:08 Sam 09 Juil 2011, 19:08 | |
| probleme109: on a cos(5x)=os(4x+x)=....... et apres quelque operations on va trouver que cos(5x)=cos(x)*(16cos²*²(x)-20cos²(x)+5). quand x=pi/10 on trouve que 0=cos(pi/2)=cos(pi/10)*(16cos²*²(pi/10)-20cos²(pi/10)+5) et on sait bien que cos(pi/10) n'est pas egale à0donc (16cos²*²(pi/10)-20cos²(pi/10)+5)=0 X=cos²(x) donc 16X²-20X+5=0 delta=400-320=80. racine de delta=4racine de5 donc X=(5-racine de5)/8 ou X=(5+racine de 5)/8 et puisque cos dalla tan9oussiya donc cos²(pi/6)<cos²(pi/10) donc X=(5+racine de 5)/8 donc cos(pi/10)=racine de((5+racine de5)/  parce que 0<pi/10<pi/2 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
