| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 28 Mai 2011, 16:42 Sam 28 Mai 2011, 16:42 | |
| - darkpseudo a écrit:
- Je parlais de continuité sur R pas en 0 .
J'ai donné le cas du zéro pour indice mais il faut constater qu'elle est continue sur IR. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 28 Mai 2011, 17:53 Sam 28 Mai 2011, 17:53 | |
| - louis a écrit:
- Problème 103:
Soit la fonction 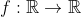 qui vérifie: qui vérifie:
\; f(x+y^{2n+1})=f(x)+(f(y))^{2n+1} \quad \forall x,y \in \mathbb{R} \text{ et } \forall n \in \mathbb{N} )
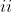\; f'(0) \ge 0)
Trouvez l'expression de ) Je réponds: On distingue entre deux cas: y=0 et y est fifférent de 0. On prends x=0, y=0, et n=0, l'équation fonctionnelle s'écrit =f(0)+(f(0))^{2\times0+1}) . Soit =f(0)+f(0)) et par conséquent =0) . Maintenant, soit y un réél différent de 0. On prends n=1, et on remplace y par 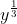 , l'équation fonctionnelle s'écrit ^{2\times1+1})=f(x)+(f(y^{\frac{1}{3}}))^{2\times1+1}) . Soit ^3)=f(x)+(f(y^{\frac{1}{3}}))^3) . Donc -f(x)=(f(y^{\frac{1}{3}}))^3) . Donc -f(x)}{y}=\frac{(f(y^{\frac{1}{3}}))^3}{y}) . Ou bien -f(x)}{y}=\frac{(f(y^{\frac{1}{3}}))^3}{(y^{\frac{1}{3}})^3}) . Soit -f(x)}{y}=\bigg(\frac{f(y^{\frac{1}{3}})}{y^{\frac{1}{3}}}\bigg)^3) .==>(*) On sait que la fonction f est dérivable en 0 d'après la seconde condition. Lorsqu'on fait tendre y vers 0, -f(x)}{y}) tendera vers ) . Et en utilisant *, on déduit que la fonction f est dérivable sur  tout entier et, en plus, la fonction f' est constante. Donc f est de la forme =k\times x) , tel que k est un réel à préciser. Réciproquement, sit f une fonction définie par =k\times x) , tel que k est un réel. Soient x et y deux rééls et n un entier. On a l'équation fonctionnelle =f(x)+(f(y))^{2n+1}) . Donc =k.x+(k.y)^{2n+1}) . Donc 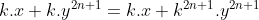 . Donc 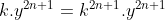 . Et puisque y est différent de 0, il s'ensuit que 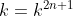 . Résolvons cette équation dans  , on a: =0\\&\Leftrightarrow k=0\text{ ou }(k^{2})^n-1=0\\&\Leftrightarrow k=0\text{ ou }(k^{2})^n=1\\&\Leftrightarrow k=0\text{ ou }k^{2}=1\\&\Leftrightarrow k=0\text{ ou }k=1\text{ ou }k=-1\\&\end{align*}) . Ainsi f(x)=x ou f(x)=0 ou f(x)=-x. Ces trois fonctions sont dérivables et de dérivées 1, 0, et -1 successivement. Mais puisque f'(0) est positif, le cas de f(x)=-x est exclus. -Synthèse: Les deux fonctions solutions au problème sont l'identité et la fonction nulle. Sauf erreur. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 31 Mai 2011, 19:57 Mar 31 Mai 2011, 19:57 | |
| - nmo a écrit:
- louis a écrit:
- Problème 103:
Soit la fonction 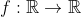 qui vérifie: qui vérifie:
\; f(x+y^{2n+1})=f(x)+(f(y))^{2n+1} \quad \forall x,y \in \mathbb{R} \text{ et } \forall n \in \mathbb{N} )
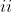\; f'(0) \ge 0)
Trouvez l'expression de ) Je réponds:
On distingue entre deux cas: y=0 et y est fifférent de 0.
On prends x=0, y=0, et n=0, l'équation fonctionnelle s'écrit =f(0)+(f(0))^{2\times0+1}) . .
Soit =f(0)+f(0)) et par conséquent et par conséquent =0) . .
Maintenant, soit y un réél différent de 0.
On prends n=1, et on remplace y par 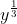 , l'équation fonctionnelle s'écrit , l'équation fonctionnelle s'écrit ^{2\times1+1})=f(x)+(f(y^{\frac{1}{3}}))^{2\times1+1}) . .
Soit ^3)=f(x)+(f(y^{\frac{1}{3}}))^3) . .
Donc -f(x)=(f(y^{\frac{1}{3}}))^3) . .
Donc -f(x)}{y}=\frac{(f(y^{\frac{1}{3}}))^3}{y}) . .
Ou bien -f(x)}{y}=\frac{(f(y^{\frac{1}{3}}))^3}{(y^{\frac{1}{3}})^3}) . .
Soit -f(x)}{y}=\bigg(\frac{f(y^{\frac{1}{3}})}{y^{\frac{1}{3}}}\bigg)^3) .==>(*) .==>(*)
On sait que la fonction f est dérivable en 0 d'après la seconde condition.
Lorsqu'on fait tendre y vers 0, -f(x)}{y}) tendera vers tendera vers ) . .
Et en utilisant *, on déduit que la fonction f est dérivable sur  tout entier et, en plus, la fonction f' est constante. tout entier et, en plus, la fonction f' est constante.
Donc f est de la forme =k\times x) , tel que k est un réel à préciser. , tel que k est un réel à préciser.
Réciproquement, sit f une fonction définie par =k\times x) , tel que k est un réel. , tel que k est un réel.
Soient x et y deux rééls et n un entier.
On a l'équation fonctionnelle =f(x)+(f(y))^{2n+1}) . .
Donc =k.x+(k.y)^{2n+1}) . .
Donc 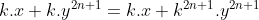 . .
Donc 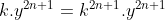 . .
Et puisque y est différent de 0, il s'ensuit que 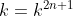 . .
Résolvons cette équation dans  , on a: , on a:
=0\\&\Leftrightarrow k=0\text{ ou }(k^{2})^n-1=0\\&\Leftrightarrow k=0\text{ ou }(k^{2})^n=1\\&\Leftrightarrow k=0\text{ ou }k^{2}=1\\&\Leftrightarrow k=0\text{ ou }k=1\text{ ou }k=-1\\&\end{align*}) . .
Ainsi f(x)=x ou f(x)=0 ou f(x)=-x.
Ces trois fonctions sont dérivables et de dérivées 1, 0, et -1 successivement.
Mais puisque f'(0) est positif, le cas de f(x)=-x est exclus.
-Synthèse:
Les deux fonctions solutions au problème sont l'identité et la fonction nulle.
Sauf erreur. Trés jolie.. Mais le passage du f'(x) constante vers f(x) = kx ne me plait pas, même si ca parait évident de remplacer f(x) par une constante dans l'ef, il fallait être discuté. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 02 Juin 2011, 16:52 Jeu 02 Juin 2011, 16:52 | |
| ça fait longtemps qu'on attend un autre problème. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 04 Juin 2011, 17:49 Sam 04 Juin 2011, 17:49 | |
| - expert_run a écrit:
- ça fait longtemps qu'on attend un autre problème.
Il reste encore cet exercice sans solution: - nmo a écrit:
- Je propose une inégalité faisant intervenir des entiers naturels:
Problème 102:
Soit n un entier naturel non nul.
Démontrez que: ^{2n}\ge(4n)^n\times(n!)^3) . .
Bonne chance. Amuse toi à le faire. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 04 Juin 2011, 19:20 Sam 04 Juin 2011, 19:20 | |
| - nmo a écrit:
- Je propose une inégalité faisant intervenir des entiers naturels:
Problème 102:
Soit n un entier naturel non nul.
Démontrez que: ^{2n}\ge(4n)^n\times(n!)^3) . .
Bonne chance. Solution du problème 102:On a :  D'après l'inégalité arithmético-géomitrique : On a : 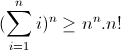 Donc  puisque:  On conclut donc que :  Et voilà. Et voilà. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 05 Juin 2011, 15:08 Dim 05 Juin 2011, 15:08 | |
| Problème 104:Soient a,b,c trois réels strictement positifs Démontrez que:  Bonne chance. Bonne chance. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 05 Juin 2011, 16:57 Dim 05 Juin 2011, 16:57 | |
| - expert_run a écrit:
- Problème 104:
Soient a,b,c trois réels strictement positifs
Démontrez que: 
Bonne chance. Bonjour, la condition a+b+c=3 ne figure-t-elle pas dans l'énoncé? | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 05 Juin 2011, 18:18 Dim 05 Juin 2011, 18:18 | |
| nn il ne figure pas dans l'énoncé. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 05 Juin 2011, 19:23 Dim 05 Juin 2011, 19:23 | |
| 2(LHS-RHS)= 2a(b-1)(c-1)+2(a-1)²+(b-c)² + (b-1)²+(c-1)², or on peut supposer b,c <=1 ou b,c>=1.
Cas d'égalité : a=b=c=1 | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 05 Juin 2011, 19:35 Dim 05 Juin 2011, 19:35 | |
| - Dijkschneier a écrit:
- 2(LHS-RHS)= 2a(b-1)(c-1)+2(a-1)²+(b-c)² + (b-1)²+(c-1)², or on peut supposer b,c <=1 ou b,c>=1.
Cas d'égalité : a=b=c=1 Et si a>=1 et b<=1 ? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 05 Juin 2011, 19:44 Dim 05 Juin 2011, 19:44 | |
| Je ne sais pas pourquoi tu proposes un problème lorsque tu n'es pas capable de comprendre sa solution ? | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 05 Juin 2011, 20:14 Dim 05 Juin 2011, 20:14 | |
| Avant tu dois parler poliment. Pour ta solution c'est exacte . Il y avait seulement un manque de concentration lors de la lecture de ta solution. | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 05 Juin 2011, 21:17 Dim 05 Juin 2011, 21:17 | |
| J'ai pas très bien compris pourquoi on peut supposer que b,c<=1 ou b,c>=1.
Une petite explication si possible... | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 05 Juin 2011, 22:20 Dim 05 Juin 2011, 22:20 | |
| Tout l'exercise 104 repose sur une serie de factorisations, donc l'inégalité est par suite équivalente à : (a-1)^2+(b-1)^2+(c-1)^2 + (a-1)(b-1)(c-1) >= 0 Si b <=1 et c >=1, prenez a <=1 et de la symétrie des rôles dans l'inégalité qu'à trouvé Dijkschneier vous trouverez que c'est juste même pour a >=1 et ainsi de suite : ) C'est le principe de la symétrie des rôles que joue b et c qui nous permet de conclure. - Dijkschneier a écrit:
- 2(LHS-RHS)= 2a(b-1)(c-1)+2(a-1)²+(b-c)² + (b-1)²+(c-1)², or on peut supposer b,c <=1 ou b,c>=1.
Cas d'égalité : a=b=c=1 C'est à vous. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 18:37 Ven 10 Juin 2011, 18:37 | |
| Il semble que Dijkschneier ne se dispose d'aucun exercice interessant pour le moment. Probléme 105:Montrer que si c'étaient a, b des entiers positives et relativement premiers entre eux, Alors qu'il existe deux entiers m et n tel qu'il soit a^m + b^n  1 (mod ab).
Dernière édition par M.Marjani le Ven 10 Juin 2011, 18:55, édité 1 fois | |
|
  | |
Mehdi.A
Maître
 Nombre de messages : 100 Nombre de messages : 100
Age : 60
Date d'inscription : 07/05/2011
 | |
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 19:10 Ven 10 Juin 2011, 19:10 | |
| - Mehdi.A a écrit:
- M.Marjani a écrit:
- Il semble que Dijkschneier ne se dispose d'aucun exercice interessant pour le moment.
Probléme 105:
Montrer que si c'étaient a et b des entiers positives relativement premiers entre eux,
Alors qu'il existe deux entiers m et n tel qu'il soit a^m + b^n  1 (mod ab). 1 (mod ab).
Marjani je te conseille de continuer ainsi tu progresse très bien en math avec ta participation en forum ,ncha2lah l'année prochaine ca serait une participation dans les OIM et tu va nous honorer avec des solution rédigé avec une aisance linguistique qui va toujours nous surprendre , Et ne t'inquiète pas pour le régional .. ton 20 en français est assuré !!  Je suppose que tu n'as pas joué dans ton enfance? A quoi est due ce retard?  Ce cours te seras utile mon cher http://www.langue-fr.net/spip.php?article47 . Malheureusement, je ne peux pas te donner un cours de quantificateurs car je sais que tu l'as bien saisie puisque t'es en MP***********************... (Respect...)  Le probléme courant: - Citation :
- Probléme 105:
Montrer que si c'étaient a, b deux entiers positives et relativement premiers entre eux,
Alors qu'il existe deux entiers m et n tel qu'il soit a^m + b^n 1 (mod ab). | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 19:28 Ven 10 Juin 2011, 19:28 | |
| Bon Marjani tu pouvais le dire de manière simple, sérieux le "si c'étaient" me met un peu mal à l'aise  et de toutes façons j'ai jamais vu jusqu'à présent une telle formulation dans l'énoncé d'un problème de mathématiques. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 19:39 Ven 10 Juin 2011, 19:39 | |
| - King a écrit:
- Bon Marjani tu pouvais le dire de manière simple, sérieux le "si c'étaient" me met un peu mal à l'aise
 et de toutes façons j'ai jamais vu jusqu'à présent une telle formulation dans l'énoncé d'un problème de mathématiques. et de toutes façons j'ai jamais vu jusqu'à présent une telle formulation dans l'énoncé d'un problème de mathématiques. ok !  L'utile c'est de comprendre ce qu'on a écrit, voilà je ne sais pas pourquoi il insiste sur ce mot-là.. | |
|
  | |
Mehdi.A
Maître
 Nombre de messages : 100 Nombre de messages : 100
Age : 60
Date d'inscription : 07/05/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 19:46 Ven 10 Juin 2011, 19:46 | |
| Moi aussi je ne sais pas pourquoi tu insiste sur ce mot la puisque tu l'a favorisé à d'autre plus simple ! en tous cas je crois que je dois m'excuser .. je ne savais pas que " si c'était" est ton nouvelle lemme .. enfin tu favorise toujours tes lemme non ? :p
Dernière édition par Mehdi.A le Ven 10 Juin 2011, 19:51, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 19:47 Ven 10 Juin 2011, 19:47 | |
| - M.Marjani a écrit:
- Il semble que Dijkschneier ne se dispose d'aucun exercice interessant pour le moment.
Probléme 105:
Montrer que si c'étaient a, b des entiers positives et relativement premiers entre eux,
Alors qu'il existe deux entiers m et n tel qu'il soit a^m + b^n  1 (mod ab). 1 (mod ab). On prend m=0 et n=1 donc b=0(mod ab) et c'est vrai, cela est valable pour tout couple d'entier (a,b). Je crois que m et n sont supposés être non nuls. Je me trompe ? Car sinon l'exercice serait trivial. | |
|
  | |
Mehdi.A
Maître
 Nombre de messages : 100 Nombre de messages : 100
Age : 60
Date d'inscription : 07/05/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 20:03 Ven 10 Juin 2011, 20:03 | |
| Mehdi tu aura mal compris l'exo .. pourtant il est bien formulé ..
b = 0 mod (ab) ???? ab divise b ???
Dernière édition par Mehdi.A le Ven 10 Juin 2011, 20:13, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 20:08 Ven 10 Juin 2011, 20:08 | |
| @Mehdi.O: Quand tu fixe b sur 0 tu transgresses le fait que a,b sont premiers entre eux. Cela implique b|a premiérement. - Spoiler:
- Mehdi.A a écrit:
- Moi aussi je ne sais pas pourquoi tu insiste sur ce mot la puisque tu l'a favorisé à d'autre plus simple ! en tous cas je crois que je dois m'excuser .. je ne savais pas que " si c'était" est ta nouvelle lemme .. enfin tu favorise toujours tes lemme non ? :p
De ce jour tu dois faire attention à ton ortographe, oui, mais c'est évident pour gagner une étoile de plus.. !!
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 10 Juin 2011, 20:15 Ven 10 Juin 2011, 20:15 | |
| - Mehdi.A a écrit:
- Mehdi tu aura mal compris l'exo .. pourtant il est bien formulé ..
b = 0 mod (ab) ???? ab divise b ??? Excusez-moi pour cette vulgaire erreur. @M.Marjani: Je n'ai pas fixé b mais le couple (m,n) et j'ai le droit vu l'existence. En outre, j'ai mal compris l'exercice. P.S: Je ne crois pas que tu auras une réponse, vu que le régional approche et il ne reste plus que 2 semaines. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
