| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Fév 2011, 11:49 Ven 11 Fév 2011, 11:49 | |
| - Dijkschneier a écrit:
- Problème 62 : (* : une étoile)
La suite f(n) définie sur IN vérifie la relation récurrente : 2[f(m+n) + f(m-n)] = f(2m) + f(2n), pour tous les entiers naturels m et n tels que m >= n, et aussi f(1)=1.
Déterminer f(1995). On a \in\mathbb{N}^2):2\big(f(m+n)+f(m-n)\big)=f(2m)+f(2n)) .==>(*) Fixons cette fois: m=n, on a: \in\mathbb{N}^2):2\big(f(m+m)+f(m-m)\big)=f(2m)+f(2m)&\Leftrightarrow(\forall m\in\mathbb{N}):2\big(f(2m)+f(0)\big)=2f(2m)\\&\Leftrightarrow(\forall m\in\mathbb{N}):2f(2m)+2f(0)=2f(2m)\\&\Leftrightarrow 2f(0)=0\\&\Leftrightarrow f(0)=0\end{align*}) . Fixons dans la relation de récurrence n=0, on a :2\big(f(m+0)+f(m-0)\big)=f(2m)+f(2\times0)&\Leftrightarrow(\forall m\in\mathbb{N}):2\big(f(m)+f(m)\big)=f(2m)+f(0)\\&\Leftrightarrow(\forall m\in\mathbb{N}):2\times 2f(m)=f(2m)+0\\&\Leftrightarrow (\forall m\in\mathbb{N}):f(2m)=4f(m)\end{align*}) . Dans la dernière relation obtenue, on remplace m par 2m, on trouve: :f(2\times2m)=4f(2m)&\Leftrightarrow(\forall m\in\mathbb{N}):f(4m)=4\times4f(m)\\&\Leftrightarrow (\forall m\in\mathbb{N}):f(4m)=16f(m)\end{align*}) . Dans *, on remplace m par 2m et n par m, on se ramène à: \in\mathbb{N}^2):2\big(f(2m+m)+f(2m-m)\big)=f(2\times2m)+f(2m)&\Leftrightarrow(\forall m\in\mathbb{N}):2\big(f(3m)+f(m)\big)=f(4m)+4f(m)\\&\Leftrightarrow(\forall m\in\mathbb{N}):2f(3m)+2f(m)=16f(m)+4f(m)\\&\Leftrightarrow (\forall m\in\mathbb{N}):2f(3m)=18f(m)\\&\Leftrightarrow (\forall m\in\mathbb{N}):f(3m)=9f(m)\end{align*}) . D'après ce qui précède, on peut conjecturer la forme générale: \in\mathbb{N}\times\mathbb{N}^*):f(a.m)=a^2.f(m)) . Démontrons ce résultat par récurrence: *Vérifier la relation pour a=1: On a =1^2.f(m)) . Ce qui est trivialement vrai. *Démonstration de l'hérédité: Supposons que la propriété est vraie au rang a et démontrons qu'elle l'est également au rang a+1. C'est à dire supposons que =a^2.f(m)) , et démontrons que .m)=(a+1)^2.f(m)) ou =(a+1)^2.f(m)) . La propriété comme je viens de dire qu'elle est vrai au rang a, donc elle est vrai au rang a-1, a-2, et ... Par conséquent, on a aussi .m)=(a-1)^2.f(m)) . Dans *, remplaçons m par am et n par m, il vient: +f(am-m)\big)=f(2\times am)+f(2m)&\Leftrightarrow2\big(f(m(a+1))+f(m(a-1))\big)=4f(am)+4f(m)\\&\Leftrightarrow2f(m(a+1))+2(a-1)^2.f(m)=4a^2.f(m)+4f(m)\\&\Leftrightarrow f(m(a+1))+(a^2-2a+1).f(m)=2a^2.f(m)+2f(m)\\&\Leftrightarrow f(m(a+1))+a^2.f(m)-2af(m)+f(m)=2a^2.f(m)+2f(m)\\&\Leftrightarrow f(m(a+1))=a^2.f(m)+2a.f(m)+f(m)\\&\Leftrightarrow f(m(a+1))=(a^2+2a+1).f(m)\\&\Leftrightarrow f(m(a+1))=(a+1)^2.f(m)\end{align*}) . Et la récurrence s'achève. Ainsi, on a démontré que \in\mathbb{N}\times\mathbb{N}^*):f(a.m)=a^2.f(m)) . Si au hasard, on choisit a=1995 et m=1, on trouve que =1995^2.f(1)) . Soit =1995^2\times1) . Finalement =1995^2) . Qui est bien sûr le résultat demandé.
Dernière édition par nmo le Sam 12 Fév 2011, 16:51, édité 2 fois (Raison : Reprendre le travail) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Fév 2011, 12:04 Ven 11 Fév 2011, 12:04 | |
| - Dijkschneier a écrit:
- Les questions trigonométriques qu'a posées M.Marjani se traitent plutôt facilement après avoir remplacé les formes trigonométriques par leurs équivalents en fonction des côtés du triangle.
Ils ne sont plus faciles, mon cher. Un exemple de ce qui est en rouge peut changer mon avis. L'exercice, d'après mon huble avis, doit être résolu. Je propose: Problème 63:Soient }) des réels connues. On suppose que ces rééls ne sont pas tous nuls. Déterminez les rééls }) qui vérifient \in\mathbb{R}^n):\sum_{k=1}^nr_k(x_k-a_k)\le\sqrt{\sum_{k=1}^nx_k^2}-\sqrt{\sum_{k=1}^na_k^2}) . Bonne chance.P.S: Un exercice qu'un camarade m'a donné.
Dernière édition par nmo le Ven 18 Fév 2011, 12:31, édité 2 fois (Raison : Changer d'exercice) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Fév 2011, 12:24 Ven 11 Fév 2011, 12:24 | |
| Ta solution au problème 62 n'est pas correcte : tu commences à faire des erreurs à partir du moment où tu dis que f(2.997m)=f(m).4^(997)
Et le problème 63 ne mérite pas d'en être un. Je te propose de le modifier. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Fév 2011, 12:30 Ven 11 Fév 2011, 12:30 | |
| - Dijkschneier a écrit:
- Ta solution au problème 62 n'est pas correcte : tu commences à faire des erreurs à partir du moment où tu dis que f(2.997)=f(m).4^(997)
Je ne trouve pas d'erreurs. Je remarque la propriété vraie pour 1, et 2 donc en répérant le même processus elle sera vraie pour 997. Pourquoi donc ce passage est érroné? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Fév 2011, 12:34 Ven 11 Fév 2011, 12:34 | |
| Le processus n'évolue pas comme ça.
Je vais t'aider un peu : la propriété correcte que tu cherches à démontrer est : f(m.2^n)=f(m).4^n ; tu peux essayer maintenant de faire une récurrence sur n, tu ne trouveras pas de problème. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Fév 2011, 12:54 Ven 11 Fév 2011, 12:54 | |
| - Dijkschneier a écrit:
- Et le problème 63 ne mérite pas d'en être un. Je te propose de le modifier.
Je vais le changer, et cette fois l'exercice sera difficile. - Dijkschneier a écrit:
- Le processus n'évolue pas comme ça.
Je vais t'aider un peu : la propriété correcte que tu cherches à démontrer est : f(m.2^n)=f(m).4^n ; tu peux essayer maintenant de faire une récurrence sur n, tu ne trouveras pas de problème. Je reprends plus tard. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 | |
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Fév 2011, 18:08 Sam 12 Fév 2011, 18:08 | |
| La methode que vous avez faites pour demontrer le probleme 62 est un peu differente que la premiere car dans la premiere vous avez constater f(am)=a²f(m) que pour les nombres pairs mais la vous avez generalise et c'est mieux a mon avis. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Fév 2011, 18:37 Sam 12 Fév 2011, 18:37 | |
| Ta solution est bonne maintenant, nmo  - nmo a écrit:
Problème 63:
Soient }) des réels connues. des réels connues.
On suppose que ces rééls ne sont pas tous nuls.
Déterminez les rééls }) qui vérifient qui vérifient \in\mathbb{R}^n):\sum_{k=1}^nr_k(x_k-r_k)\le\sqrt{\sum_{k=1}^nx_k^2}-\sqrt{\sum_{k=1}^na_k^2}) . .
Bonne chance.
P.S: Un exercice qu'un camarade m'a donné. Solution au problème 63 :Voyons ce qui a lieu pour de petites valeurs de n. - Si n=1 : On veut déterminer r tel que r(x-r) <= |x| - |a| pour tout réel x. On distingue bien sûr deux cas : si x est positif, et s'il est négatif. S'il est positif, alors ce qu'on a est : x(1-r)+r²-|a|>=0 pour tout x positif. Pour que cela soit effectivement vrai pour tout réel positif, il est nécessaire et suffisant que 1-r >= 0 et r²-|a|>=0, c'est-à-dire, 1>=r et r²>=|a|. De même, en étudiant le cas négatif, on obtient : -1<=r et r²>=|a|. Ainsi, si n=1, il est nécessaire et suffisant que sqrt(|a|)<=|r|<=1. Il suffit par conséquent de choisir un r qui vérifie sqrt(|a|)<=|r|<=1 pour qu'on soit bon. Remarquons toutefois que la condition sqrt(|a|)<=1 sur a est nécessaire. Bien. - Si n=2 : La situation est un peu plus compliquée : on veut déterminer r_1 et r_2 tels que : %20+%20r_2%20(x_2%20-%20r_2)%20\leq%20\sqrt{x_1%20^2%20+%20x_2%20^2}%20-%20\sqrt{a_1%20^2%20+%20a_2%20^2}) , pour tous réels x_1 et x_2 En prenant x_2 = 0 et en étudiant les cas positifs et négatifs pour x_1, puis en considérant aussi la situation symétrique de celle-ci, on obtient de même que précédemment une condition nécessaire :  , et  Mais cette condition n'est maintenant pas suffisante. On peut suggérer par contre une condition suffisante, qui est :  et  , car alors, nous aurons : %20+%20r_2%20(x_2%20-%20r_2)%20\leq%20\sqrt{x_1%20^2%20+%20x_2%20^2}%20-%20\sqrt{a_1%20^2%20+%20a_2%20^2}%20\\%20\Leftrightarrow%20(\sqrt{x_1%20^2%20+%20x_2%20^2}%20-%20r_1%20x_1%20+%20r_2%20x_2%20)%20+%20(r_1%20^2%20+%20r_2%20^2%20-%20\sqrt{a_1%20^2%20+%20a_2^2})%20\geq%200) , ce qui est vrai puisque  et (r_1^2%20+%20r_2^2)}%20\geq%20r_1%20x_1%20+%20r_2%20x_2) d'après l'inégalité de Cauchy-Schwarz. Il suffit par conséquent de choisir r_1 et r_2 qui vérifient les conditions précédentes pour qu'on soit bon. Mais on a imposé la condition  qui n'est peut-être pas nécessaire ; mais  est nécessaire. - Si n est quelconque : On peut voir que la méthode précédente pour n=2 ne change pas beaucoup. De même on prouve qu'il suffit de choisir ) qui vérifient :  pour qu'on soit bon. Mais on aura imposé une condition  qui ne serait peut-être pas nécessaire ; par contre,  est nécessaire. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Fév 2011, 19:27 Sam 12 Fév 2011, 19:27 | |
| Pour le Probleme 58 de M.Marjani: (ii)on a +sin^{2}(\frac{B}{2})+sin^{2}(\frac{C}{2})=\frac{1-cos(A)}{2}+\frac{1-cos(B)}{2}+\frac{1+cos(A+B)}{2}) et *sin(\frac{B}{2})*sin(\frac{C}{2})=(cos(\frac{A-B}{2})-cos(\frac{A+B}{2}))*cos(\frac{A+B}{2})) alors *sin(\frac{B}{2})*sin(\frac{C}{2})=\frac{cos(A)+cos(B)}{2}-\frac{cos(A+B)+1}{2}) finalement +sin^{2}(\frac{B}{2})+sin^{2}(\frac{C}{2})+2sin(\frac{A}{2})*sin(\frac{B}{2})*sin(\frac{C}{2})=1) C.Q.F.D sauf erreur  | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Fév 2011, 19:32 Sam 12 Fév 2011, 19:32 | |
| j'aimerais bien une confirmation pour ma solution! et d'en proposer d'autres mieux que celle ci.amicalement  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 13 Fév 2011, 14:50 Dim 13 Fév 2011, 14:50 | |
| Je crois que ta solution, yasserito, est la meilleure en termes de nombres de lignes.
En attente d'une confirmation de ma précédente solution, je propose un autre problème :
Problème 64 : (*** : trois étoiles)
Plusieurs entiers naturels non nuls sont écrits au tableau.
On se permet à chaque étape de choisir deux entiers et de les remplacer par leur pgcd et par leur ppcm.
Prouver que finalement, peu importe les deux nombres choisis, l'opération décrite plus haut ne produit plus aucun changement. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 12:53 Mer 16 Fév 2011, 12:53 | |
| - Dijkschneier a écrit:
- Je crois que ta solution, yasserito, est la meilleure en termes de nombres de lignes.
Bien, et on a aussi la relation suivante pour n'importe quel triangle dont on symbolise les amplitudes de ses angles par A, B, et C:  . Et ce qui est cette fois facile à démontrer. - Citation :
- En attente d'une confirmation de ma précédente solution.
Désolé pour le retard. Vraiment, j'ai lu soigneusement ta solution, mais je ne sais quoi dire! Si je dis que c'est faux, ce serait de l'injustice, au moins pour l'effort que tu as fait. Si je dis que c'est correct, ce serais un gete flatteur. Peût-être, il faut changer de question et dire plus précisément: - nmo a écrit:
- Problème 63:
Soient }) des réels connues. des réels connues.
On suppose que ces rééls ne sont pas tous nuls.
Déterminez les rééls }) qui vérifient qui vérifient \in\mathbb{R}^n):\sum_{k=1}^nr_k(x_k-a_k)\le\sqrt{\sum_{k=1}^nx_k^2}-\sqrt{\sum_{k=1}^na_k^2}) , en fonction des rééls , en fonction des rééls }) . . Je te fais part de ce j'ai en tête plus tard. Cordialement.
Dernière édition par nmo le Ven 18 Fév 2011, 12:30, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 13:17 Mer 16 Fév 2011, 13:17 | |
| - nmo a écrit:
- nmo a écrit:
- Dijkschneier a écrit:
- Le processus n'évolue pas comme ça.
Je vais t'aider un peu : la propriété correcte que tu cherches à démontrer est : f(m.2^n)=f(m).4^n ; tu peux essayer maintenant de faire une récurrence sur n, tu ne trouveras pas de problème. Je reprends plus tard. C'est fait, tu peux me donner ton avis maintenant.
Le problème courant, en plus des questions trigonométriques, est celui-ci
- nmo a écrit:
- Problème 63:
Soient }) des réels connues. des réels connues.
On suppose que ces rééls ne sont pas tous nuls.
Déterminez les rééls }) qui vérifient qui vérifient \in\mathbb{R}^n):\sum_{k=1}^nr_k(x_k-r_k)\le\sqrt{\sum_{k=1}^nx_k^2}-\sqrt{\sum_{k=1}^na_k^2}) . .
Bonne chance.
P.S: Un exercice qu'un camarade m'a donné. La solution de cet exercice est présente dans DIMA DIMA : Page :393. On prend au début x_1=x_2=....=x_n=0 donc V(Sigma a_k²) < Sigma(r_k.a_k) ==> (1) En prenant : x_k=2a_k V(Sigma a_k²)> Sigma(r_k.a_k) => (2) de (1) et (2) on conclut que V(Sigma a_k²)= Sigma(r_k.a_k) Ainsi en prenant x_k=r_k et en applicant Cauchy - Schwarz et en remplacant dans la 1ere inéquaton on trouve : V(Sigma r_k²)=1 ainsi r_k=b.a_k. Ainsi r_i=a_i/(V(Sigma a_k²) | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 13:25 Mer 16 Fév 2011, 13:25 | |
|
Dernière édition par Mehdi.O le Mer 16 Fév 2011, 15:22, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 13:32 Mer 16 Fév 2011, 13:32 | |
| - Mehdi.O a écrit:
On prend au début x_1=x_2=....=x_n=0
donc V(Sigma a_k²) < Sigma(r_k.a_k) ==> (1)
??! x_1=x_2=....=x_n=0 donne V(Sigma a_k²) <= V(Sigma r_k²) Et on ne propose pas de problème vite fait ici. On commence par voir si un problème est déjà posté. Si ce n'est pas le cas, on propose notre problème en le numérotant. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 14:18 Mer 16 Fév 2011, 14:18 | |
| On a pour tout x_i c'est comme une E.F, on peut prendre des valeurs !!! Bon j'ai pas utilisé Latex, ca serait nettement mieux! La solution figure dans Dima dima si tu désires la voir  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 14:25 Mer 16 Fév 2011, 14:25 | |
| Que ce soit dans un quelconque livre ou pas (je ne possède d'ailleurs pas le livre que tu cites), elle demeure ambigüe...
Je dis que x_1=x_2=....=x_n=0 donne V(Sigma a_k²) <= V(Sigma r_k²)
Quelle est ta réponse ? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 14:36 Mer 16 Fév 2011, 14:36 | |
| Oui je vais te répondre : L'énoncé qu'a donné nmo est erroné dans la pârtie d'à gauche ce n'est pas : r_k(x_k-r_k) mais plutôt : r_k(x_k-a_k) c'est ce qui était ambigü pour toi je crois, ce qui reste c'est facile  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 15:00 Mer 16 Fév 2011, 15:00 | |
| Merci Mehdi.O.
Je te prie maintenant de numéroter ton dernier problème : problème 65. Au mieux, je te propose d'en proposer un autre, car celui que tu proposes est bien connu.
On pourra revenir sur le problème 64 ultérieurement. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 15:21 Mer 16 Fév 2011, 15:21 | |
| Bien Dijkschneier je le supprime maintenant.
Voici un exercice maintenant :
Problème 65 :
Soit R l’ensemble des nombres réels. Déterminer toutes les fonctions f : R => R vérifiant :
f(x+y) <= f(x) + f(y)<= x+y pour tous x et y réels. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 16:15 Mer 16 Fév 2011, 16:15 | |
| Solution au problème 65 :
Soit P(x,y) la proposition : f(x+y) <= f(x) + f(y)<= x+y
P(0,0) ==> f(0) <= 2f(0) <= 0 ==> f(0)=0
P(x,-x) ==> f(0) <= f(x)+f(-x) <= 0 ==> f(-x)=-f(x)
P(x/2,x/2) ==> f(x)<=2f(x/2) <= x ==> f(x) <= x
Soit Q(x) la proposition : f(x) <= x
Q(-x) ==> f(-x) <= -x ==> -f(x) <= -x ==> f(x) >= x
Puisque f(x)>=x et f(x)<=x, alors f(x)=x.
Synthèse :
La seule solution à l'EF est l'identité. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 17:01 Mer 16 Fév 2011, 17:01 | |
| je crois que j'ai trouve la meme solution: f est une identite! juste peut on pour trouver que f(x)<=x dire que on a f(x+y)<=x+y alors f(x)<=x ? amicalement  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 17:59 Mer 16 Fév 2011, 17:59 | |
| Problème 66 : (** : deux étoiles)
Trouver tous les triplets (x,y,z) de [0,1]^3 tels que :
x²+y²+z²+2xyz=1. | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Fév 2011, 20:29 Mer 16 Fév 2011, 20:29 | |
| - Dijkschneier a écrit:
- Je crois que ta solution, yasserito, est la meilleure en termes de nombres de lignes.
En attente d'une confirmation de ma précédente solution, je propose un autre problème :
Problème 64 : (*** : trois étoiles)
Plusieurs entiers naturels non nuls sont écrits au tableau.
On se permet à chaque étape de choisir deux entiers et de les remplacer par leur pgcd et par leur ppcm.
Prouver que finalement, peu importe les deux nombres choisis, l'opération décrite plus haut ne produit plus aucun changement. On pose a et b les deux nombres choisis. Soit les suites récurrentes ) et ) définies par :  et  Nous avons :  et  . Nous avons : }p_2^{max(\alpha_2,\beta_1)}...p_n^{max(\alpha_n,\beta_n)}) et }p_2^{min(\alpha_2,\beta_1)}...p_n^{min(\alpha_n,\beta_n)}) Nous avons : ,min(\alpha_1,\beta_1))}p_2^{max(max(\alpha_2,\beta_2),min(\alpha_2,\beta_2))}...p_n^{max(max(\alpha_n,\beta_n),min(\alpha_n,\beta_n))}) et ,min(\alpha_1,\beta_1))}p_2^{min(max(\alpha_2,\beta_2),min(\alpha_2,\beta_2))}...p_n^{min(max(\alpha_n,\beta_n),min(\alpha_n,\beta_n))}) Nous savons que ,min(x_1,x_2))=max(x_1,x_2)) et ,min(x_1,x_2))=min(x_1,x_2)) De ce fait, 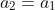 et 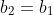 Les deux suites sont donc constantes à partir de n=1, ce qui conclut. Sauf erreur. Au plaisir ! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
