| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Déc 2010, 09:51 Ven 17 Déc 2010, 09:51 | |
| - yasserito a écrit:
- Personnellement je crois que j'ai prouver que 0 est une solution a fof(0)=0 et j'ai prouver son unicite mais est ce le faite que f est une bijection nous perment de dire quef(0)=0?
et si oui, svp expliquez, et desolé pour aucun derangement. Oui, tu peux dire que f(0)=0 si f est bijective de IR vers IR, ce qui nécessite une démonstration: Tu peux remarqué qu'on a juste démontré que fof est bijective de IR* vers IR*. Donc, on a fof(IR*)=IR*. D'autre part, on sait que =g(A)\cup g(B)) . Posons A=IR* et B={0} et g=fof. Donc fof(IR* 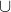 {0})=fof(IR*) 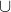 fof({0}). Donc fof(IR)=IR* 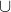 {0}. Enfin fof(IR)=IR. Donc f est bijective de IR vers IR. CQFD. P.S: Oublions cet exercice, et passons à d'autres choses. Je crois que les réponses autour l'exercice sont assez suffisantes. Si tu n'es pas satisfait, tu peux créer un autre topic de débat. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 17 Déc 2010, 11:41 Ven 17 Déc 2010, 11:41 | |
| - nmo a écrit:
- Problème 30:
On considère un point P à l'intérieur d'un rectangle ABCD tel que les distances AP, BP, et CP soient proportionnelles aux nombres 1, 2, et 3 respectivement.
Trouvez la mesure de l'angle APB. Voici ma solution: Posons AB=a et APB=x et AP=z. On a AP, BP, et CP sont proportionnelles aux nombres 1, 2, et 3 respectivement. Donc  . Donc BP=2AP. Donc BP=2z. Et selon la loi des sinus dans le triangle APB, on a  . Donc  . Donc  .==>(1) Selon le théorème d'Alkashi, on a  . Donc ^2-2*z*2z*\cos{x}) . Donc  . Donc  . Donc  . Donc  .==>(2) Et selon le théorème d'Alkashi, on a  . Donc ^2=z^2+a^2-4z^2*\cos{PAB}) . Donc  . Donc  . Donc  . Donc  .==>(3) De 1, on a  . Donc \frac{a^2}{4z^2}) . Et selon 2 et 3, ^2=(1-\big(\frac{a^2-3z^2}{4z^2}\big)^2)*\frac{a^2}{4z^2}) . Donc (1+\frac{5z^2-a^2}{4z^2})=(1-\frac{a^2-3z^2}{4z^2})(1+\frac{a^2-3z^2}{4z^2})\frac{a^2}{4z^2}) . Donc (\frac{9z^2-a^2}{4z^2})=(\frac{7z^2-a^2}{4z^2})(\frac{a^2+z^2}{4z^2})*\frac{a^2}{4z^2}) . Donc (9z^2-a^2)=a^2(7z^2-a^2)(a^2+z^2)) . Donc =a^2(7z^2a^2+7z^4-a^4-a^2z^2)) . Donc =a^2(6z^2a^2+7z^4-a^4)) . Donc  . Donc  . Donc  . Donc  . Donc  . Donc -4z^2(a^4-6a^2z^2+9z^4)=0) . Donc (a^4-6a^2z^2+9z^4)=0) . Donc (a+2z)(a^2-3z^2)^2=0) . Donc 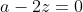 , ou 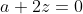 , ou  . Donc 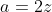 , ou 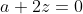 , ou (a+\sqrt{3}z)=0) . Donc  , ou 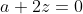 , ou  , ou  . Donc 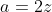 , ou  . (Une disatnce est toujours positive). Le premier cas: 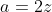 . Donc  . Et selon 1, on a  . Donc  . Donc  . Donc  . Donc  . (A l'aide de la calculatrice). Le second cas:  . Donc  . Et selon 1, on a  . Donc  . Donc  . Donc  . Donc  . (A l'aide du cercle trigonométrique). CQFD. P.S: C'était un exercice tiré d'un olympiade de terminale, année 1998. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 19 Déc 2010, 12:26 Dim 19 Déc 2010, 12:26 | |
| - Dijkschneier a écrit:
- Problème 34 : (* : une étoile)
Soit n un entier et x un réel.
Montrer que : %20=%20E(nx)) , où E(x) désigne la partie entière de x. , où E(x) désigne la partie entière de x. Je réponds: Soit q et r le quotient et le reste de la division euclédienne de ) sur n, respectivement. On a =nq+r) , et q et r sont des entiers, et  .==>(1) On a \le nx< E(nx)+1) . Donc }{n}\le x< \frac{E(nx)+1}{n}) . Donc  . Donc  . Donc  . La relation etablie est valable pour tout k vérifiant  .==>(2) On distingue par la suite deux cas: Cas premier:  . On a  . Donc  . Donc  . Donc =q) . Cas deuxième:  . On a  . Donc  . Donc  . Donc  . Et on a, en sommant 1 et 2,  . Donc  . Donc  . Et on a  . Donc  . On a  . Donc  . Donc =q+1) . Passons au sérieux: On a =\sum_{k=0}^{n-r-1}E(x+\frac{k}{n})+\sum_{k=n-r}^{n-1}E(x+\frac{k}{n})) . Donc =(n-r)q+r(q+1)) , en tenant compte de ce qui précède. Donc =nq-rq+rq+r) . Donc =nq+r) . Donc =E(nx)) . CQFD. Sauf erreur.
Dernière édition par nmo le Lun 20 Déc 2010, 17:00, édité 2 fois (Raison : Correction) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 19 Déc 2010, 12:40 Dim 19 Déc 2010, 12:40 | |
| Problème 35:Soit c un réel strictement positif, et a et b sont deux réels vérifiant a>c et b>c. Démontrez que }+\sqrt{c(b-c)}) , et précisez le cas dégalité. Bonne chance. | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 19 Déc 2010, 13:56 Dim 19 Déc 2010, 13:56 | |
| on a √ab≥√(c(a-c)) +√(c(b-c)) <---> ab≥c(a+b-2c+2√((a-c)(b-c))
<---> ab≥c[(√(a-c) + √(b-c))]² *
on a (√(ab/c))/2≥√(a-c) ou √(b-c) celui ci donne que l'expression* est vrai
| |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 19 Déc 2010, 14:36 Dim 19 Déc 2010, 14:36 | |
| Heu peut tu donné plus d'explication pour la dérnière ligne stp ? | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 19 Déc 2010, 19:50 Dim 19 Déc 2010, 19:50 | |
| je m'excuse je crois que j'ai un erreur je réviserai ma solution | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 19 Déc 2010, 21:37 Dim 19 Déc 2010, 21:37 | |
| @nmo : bravo pour ta solution au problème 34. Pour expliquer un peu, le problème consiste à dénombrer les parties entières valant [x] et ceux valant [x] + 1 et d'en faire la somme. Solution au problème 35 :Selon CS : )((b-c)+c)}%20\geq%20\sqrt{c(b-c)}%20+%20\sqrt{c(a-c)}) Problème 36 : Problème 36 : (** : deux étoiles) Soit f : [0,1] -> R+ une fonction telle que f(1)=1 et : f(x+y) >= f(x)+f(y) dès que x,y,x+y sont dans [0,1]. Montrer que f(x) <= 2x, pour tout x appartenant à [0,1].
Dernière édition par Dijkschneier le Lun 20 Déc 2010, 13:18, édité 1 fois | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 19 Déc 2010, 22:01 Dim 19 Déc 2010, 22:01 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 20 Déc 2010, 16:57 Lun 20 Déc 2010, 16:57 | |
| - mizmaz a écrit:
- Petite erreur de cas ?
Non, c'est une faute d'inattention. Maintenant, c'est édité. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 20 Déc 2010, 17:25 Lun 20 Déc 2010, 17:25 | |
| - Dijkschneier a écrit:
- Solution au problème 35 :
Selon CS : )((b-c)+c)}%20\geq%20\sqrt{c(b-c)}%20+%20\sqrt{c(a-c)}) Une solution alternative consiste à remarquer que l'inégalité est équivalente à quelque chose vraie: +c^2}-c)^2\ge0) , après élever au carré bien sûr. Le cas d'égalité saute aux yeux. C'est en effet, lorsque  . | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 21 Déc 2010, 20:27 Mar 21 Déc 2010, 20:27 | |
|
est ce que il nya pas aucune réponse pour la problème 36
j'ai essayé mais en vain
| |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 22 Déc 2010, 02:41 Mer 22 Déc 2010, 02:41 | |
| Solution au probléme 36:
Bienvu : 0=<1-y=<1 <=> 0=<y=<1 (A). Donc P(x,y): f(x+y)>=f(x)+f(y) => P(1-y,y): 1>=f(y)+f(1-y) (C).
Selon (C): f(x)=<1-f(1-x). On suppose que f(x)>2x (1) , donc 2x<f(x)=<1-f(1-x) donc f(1-x)<1-2x
On pose 1-x=X avec X£[0,1] selon (A), donc f(x)<1-2(1-x) ==> f(x)<2x-1 ==> contradiction avec notre supposition (1). D'ou f(x)>=2x.
Réciproquement: 2(x+y)>=f(x+y)>=f(x)+f(y). Or 2(x+y)=2x+2y>=f(x)+f(y) ce qui est juste.
CQFD.
Dernière édition par M.Marjani le Sam 25 Déc 2010, 13:41, édité 5 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 22 Déc 2010, 12:44 Mer 22 Déc 2010, 12:44 | |
| - M.Marjani a écrit:
- f:[0,1]-->IR+ donc 0=<f(y)=<1.
Je ne comprends pas ce donc. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 22 Déc 2010, 17:31 Mer 22 Déc 2010, 17:31 | |
| - Dijkschneier a écrit:
- M.Marjani a écrit:
- f:[0,1]-->IR+ donc 0=<f(y)=<1.
Je ne comprends pas ce donc. Je comprend deux sens dans votre intervention, bon ce n'est qu'une faute de réecriture. Elle se voit inutile dans la démonstration mais quand méme utile pour vérifier le résultat f(x)=<2x. - Spoiler:
Pour le passage: Car 1-f(1-y)>=0 et ((1-y),x) £ [0,1]² qu'on peut poser 1-y=x. 1-f(x)>=0 donc f(x)=<1 pour tout x dans [0,1]. Par consequent 0=<f(y)=<1 car f:[0,1] --> IR+. [Une tite remarque consiste de dire que si f(x)>=1 implique ne pas arrivé à notre résultat géneral pour x qui est f(x)=<2x : )
C'est édité. Je n'ai pas un probléme de bon niveau à proposer donc je laisse la liberté à tous pour proposer un. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 22 Déc 2010, 18:15 Mer 22 Déc 2010, 18:15 | |
| - M.Marjani a écrit:
- Ma solution du probléme 36:
Réccurence immédiate, nous permet de conclure que: f(ax)>=af(x) / a£[0;1] (A)
- Spoiler:
Supposons que pour tout a£[0,1] f(ax)>=af(x). Ce qui reste à demontrer: f((a+1)x)-(a+1)f(x)>=0.
On a selon (1) P(x,ax): f((a+1)x)=f(x+(ax))>=f(x)+f(ax)>=f(x)+af(x)=(a+1)f(x). Ce qui est juste.
Alors f(x*1)>=x*f(1)=x donc f(x)>=x. Et Bienvu : 0=<1-y=<1 <=> 0=<y=<1.
P(x,y): f(x+y)>=f(x)+f(y) => P(1-y,y): 1>=f(y)+f(1-y) (C). On sait que f(1-x)>=1-x>=1-x-x=1-2x donc f(x)=<1-f(1-x)=<2x (Selon (C)).
CQFD. Ta démonstration est incorrecte dans le sens où tu ne peux pas démontrer par récurrence que pour tout réel x de [0,1], et tout réel a de [0,1], tels que ax soit de [0,1] : f(ax) >= af(x). On a des réels ici, pas des entiers. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 22 Déc 2010, 19:24 Mer 22 Déc 2010, 19:24 | |
| - Dijkschneier a écrit:
- M.Marjani a écrit:
- Ma solution du probléme 36:
Réccurence immédiate, nous permet de conclure que: f(ax)>=af(x) / a£[0;1] (A)
- Spoiler:
Supposons que pour tout a£[0,1] f(ax)>=af(x). Ce qui reste à demontrer: f((a+1)x)-(a+1)f(x)>=0.
On a selon (1) P(x,ax): f((a+1)x)=f(x+(ax))>=f(x)+f(ax)>=f(x)+af(x)=(a+1)f(x). Ce qui est juste.
Alors f(x*1)>=x*f(1)=x donc f(x)>=x. Et Bienvu : 0=<1-y=<1 <=> 0=<y=<1.
P(x,y): f(x+y)>=f(x)+f(y) => P(1-y,y): 1>=f(y)+f(1-y) (C). On sait que f(1-x)>=1-x>=1-x-x=1-2x donc f(x)=<1-f(1-x)=<2x (Selon (C)).
CQFD. Ta démonstration est incorrecte dans le sens où tu ne peux pas démontrer par récurrence que pour tout réel x de [0,1], et tout réel a de [0,1], tels que ax soit de [0,1] : f(ax) >= af(x). On a des réels ici, pas des entiers. Bleu: Non ce n'est pas nécessairement, je peux démontrer f(x)>=x et laisser tomber f(ax)>=af(x). Supposons que f(ax)>=af(x). Ce qui reste à démontrer: f((a+t)x)>=(a+t)f(x) pour tout (t) £[0,1]² tel que a+t=<1. On a f((a+t)x)=f(ax+tx)>=f(ax)+f(tx)>=af(x)+tf(x)=(a+t)f(x). Ce qui est juste. Si ce qui est demandé.. ? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 23 Déc 2010, 17:35 Jeu 23 Déc 2010, 17:35 | |
| On a des réels ici, pas des entiers. Tu ne peux pas parler de "récurrence". | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 23 Déc 2010, 18:26 Jeu 23 Déc 2010, 18:26 | |
| - M.Marjani a écrit:
- Bleu: Non ce n'est pas nécessairement, je peux démontrer f(x)>=x et laisser tomber f(ax)>=af(x).
Je trouve le résultat que tu veux démontrer est faux. Voici un contre exemple, 1/2>=f(1/2), en posant x=y=1/2. A toi de revoir ton travail. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 23 Déc 2010, 22:37 Jeu 23 Déc 2010, 22:37 | |
| @Dijkschneier: J'ai déjà vu des réccurences sur les réels. Peut-étre que t'as raison, j'en ai aucune idée. - nmo a écrit:
- M.Marjani a écrit:
- Bleu: Non ce n'est pas nécessairement, je peux démontrer f(x)>=x et laisser tomber f(ax)>=af(x).
Je trouve le résultat que tu veux démontrer est faux.
Voici un contre exemple, 1/2>=f(1/2), en posant x=y=1/2.
A toi de revoir ton travail. Ce n'est pas une forte preuve. Ca peut étre f(1/2)=1/2  donne moi un deuxiéme contre exemple et je renonce ^^ Je laisse la main. Je reprend plus tard peut-étre. : ) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 24 Déc 2010, 12:06 Ven 24 Déc 2010, 12:06 | |
| - M.Marjani a écrit:
- @Dijkschneier: J'ai déjà vu des réccurences sur les réels. Peut-étre que t'as raison, j'en ai aucune idée.
- nmo a écrit:
- M.Marjani a écrit:
- Bleu: Non ce n'est pas nécessairement, je peux démontrer f(x)>=x et laisser tomber f(ax)>=af(x).
Je trouve le résultat que tu veux démontrer est faux.
Voici un contre exemple, 1/2>=f(1/2), en posant x=y=1/2.
A toi de revoir ton travail. Ce n'est pas une forte preuve. Ca peut étre f(1/2)=1/2  donne moi un deuxiéme contre exemple et je renonce ^^ donne moi un deuxiéme contre exemple et je renonce ^^
Je laisse la main. Je reprend plus tard peut-étre. : ) La fonction f(x)=x^3, qui satisfait l'énoncé, ne satisfait pas f(x)>=x pour tout x de [0,1]. A toi de voir, et de rectifier. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 25 Déc 2010, 00:00 Sam 25 Déc 2010, 00:00 | |
| - nmo a écrit:
- M.Marjani a écrit:
- @Dijkschneier: J'ai déjà vu des réccurences sur les réels. Peut-étre que t'as raison, j'en ai aucune idée.
- nmo a écrit:
- M.Marjani a écrit:
- Bleu: Non ce n'est pas nécessairement, je peux démontrer f(x)>=x et laisser tomber f(ax)>=af(x).
Je trouve le résultat que tu veux démontrer est faux.
Voici un contre exemple, 1/2>=f(1/2), en posant x=y=1/2.
A toi de revoir ton travail. Ce n'est pas une forte preuve. Ca peut étre f(1/2)=1/2  donne moi un deuxiéme contre exemple et je renonce ^^ donne moi un deuxiéme contre exemple et je renonce ^^
Je laisse la main. Je reprend plus tard peut-étre. : ) La fonction f(x)=x^3, qui satisfait l'énoncé, ne satisfait pas f(x)>=x pour tout x de [0,1].
A toi de voir, et de rectifier. Oui t'as raison. J'ai trompé là-bas. Dans f(x*1)>=x*f(1) . Il m'a fallut plutot dire que f(x*1)>=1*f(x) car f(ax)>=af(x) bon. Ainsi ma solution est erroné du début, comme l'a dit Dijkschneier, que la réccurence serait sur des entiérs. Je laisse la main. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 25 Déc 2010, 12:27 Sam 25 Déc 2010, 12:27 | |
| - M.Marjani a écrit:
- @Dijkschneier: J'ai déjà vu des réccurences sur les réels. Peut-étre que t'as raison, j'en ai aucune idée.
La récurrence est un concept propre aux entiers  . | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 25 Déc 2010, 13:34 Sam 25 Déc 2010, 13:34 | |
| - Dijkschneier a écrit:
- M.Marjani a écrit:
- @Dijkschneier: J'ai déjà vu des réccurences sur les réels. Peut-étre que t'as raison, j'en ai aucune idée.
La récurrence est un concept propre aux entiers  . . Oui j'ai fais une cline d'oeuil sur le concept. XD Bon j'ai réctifié: Solution 36:Bienvu : 0=<1-y=<1 <=> 0=<y=<1 (A). Donc P(x,y): f(x+y)>=f(x)+f(y) => P(1-y,y): 1>=f(y)+f(1-y) (C). Selon (C): f(x)=<1-f(1-x). On suppose que f(x)>2x (1) , donc 2x<f(x)=<1-f(1-x) donc f(1-x)<1-2x On pose 1-x=X avec X£[0,1] selon (A), donc f(x)<1-2(1-x) ==> f(x)<2x-1 ==> contradiction avec notre supposition (1). D'ou f(x)=<2x. Réciproquement: 2(x+y)>=f(x+y)>=f(x)+f(y). Or 2(x+y)=2x+2y>=f(x)+f(y) ce qui est juste. CQFD. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 26 Déc 2010, 12:50 Dim 26 Déc 2010, 12:50 | |
| - M.Marjani a écrit:
- Dijkschneier a écrit:
- M.Marjani a écrit:
- @Dijkschneier: J'ai déjà vu des réccurences sur les réels. Peut-étre que t'as raison, j'en ai aucune idée.
La récurrence est un concept propre aux entiers  . .
Oui j'ai fais une cline d'oeuil sur le concept. XD
Bon j'ai réctifié:
Solution 36:
Bienvu : 0=<1-y=<1 <=> 0=<y=<1 (A). Donc P(x,y): f(x+y)>=f(x)+f(y) => P(1-y,y): 1>=f(y)+f(1-y) (C).
Selon (C): f(x)=<1-f(1-x). On suppose que f(x)>2x (1) , donc 2x<f(x)=<1-f(1-x) donc f(1-x)<1-2x
On pose 1-x=X avec X£[0,1] selon (A), donc f(x)<1-2(1-x) ==> f(x)<2x-1 ==> contradiction avec notre supposition (1). D'ou f(x)=<2x.
Réciproquement: 2(x+y)>=f(x+y)>=f(x)+f(y). Or 2(x+y)=2x+2y>=f(x)+f(y) ce qui est juste.
CQFD. Tu as f(x)>2x et f(x)<2x-1, mais il n'y a pas de contradiction, puisque ce n'est pas le même x... J'ai l'impression que tu cherches à rendre correcte une démonstration qui ne l'est pas... Comme cela fait une semaine qu'une solution n'est pas proposée, on passe à un nouveau problème. Solution au problème 36 :Pour tous y > x, f(y) > f(x)+f(y−x) > f(x), donc f est croissante. Par ailleurs, une récurrence immédiate donne %20\leq%202^{-k}) pour tout entier k. Pour x appartenant à ]0, 1], soit un entier k tel que }) ; alors %20\leq%20f(2^{-(k-1)})%20\leq%202^{-(k-1)}%20%3C%202x) . Et comme f(0) + f(1) <= f(1), on a f(0) = 0 et donc f(x) <= 2x dans tous les cas. Problème 37 : (** : deux étoiles) Montrer que pour tout entier naturel n non nul, 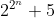 n'est jamais un nombre premier. Attention, les puissances sont en étage.
Dernière édition par Dijkschneier le Dim 26 Déc 2010, 16:34, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
