| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Mar 2011, 18:19 Sam 12 Mar 2011, 18:19 | |
| - boubou math a écrit:
- Salut
JE poste une autre solution d'exo 77
a>b+c d'ou 2a>2 a>1 de meme b>1 et c>1 d'ou (a-1)(1-b)(1-c)<0
a+b+c-ab-ac-bc+abc-1<0
1-ab-ac-bc+abc<0
d'une autre part (a+b+c)²=a²+b²+c²+2(ab+ac+bc)=4
ab+ac+bc=(4-a²-b²-c²)/2
l'inégalité devient 1-(4-a²-b²-c²)/2 + abc<0
2+a²+b²+c²-4+2abc<0
a²+b²+c²+2abc<2
AMICALEMENT . T'as inversé les signes  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Mar 2011, 18:23 Sam 12 Mar 2011, 18:23 | |
| oué faute de frappe  sinon la reponsse est juste  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Mar 2011, 19:02 Sam 12 Mar 2011, 19:02 | |
| Problème 78:
Soit ABC un triangle et h l'hauteur issue de A. On note x=<BAC
i) Montrez que AB+AC>= BC.cosx + 2h.sinx
ii) Montrez le cas d'égalité | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Mar 2011, 19:18 Sam 12 Mar 2011, 19:18 | |
| J'attends le problème 79 puisqu'on se comprend... | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Mar 2011, 19:33 Sam 12 Mar 2011, 19:33 | |
| Problème 79:
On considère un triangle ABC . Le demi cerlce de diamètre BC coupe les côtés AB et AC en D et E respectivement, soient F et G les projections ortogonales de D et E sur BC. Les droites EF et DG se coupent en M.
Montrez que les droites BC et AM sont perpediculaires
| |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Mar 2011, 19:37 Sam 12 Mar 2011, 19:37 | |
| Voici un problème de plus et qui est intéressant.
Problème 80 :
Soit a,b,c et d des réels positives . Montrer que :
(*) (a^5-a²+3)(b^5-b²+3)(c^5-c²+3) >= (a+b+c)^3 .
(**) (a+b)^3 (b+c)^3 (c+d)^3 (d+a)^3 ≥ 16a^2b^2c^2d^2 (a+b+c+d)^4
Dernière édition par M.Marjani le Dim 13 Mar 2011, 00:37, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 16 Mar 2011, 17:23 Mer 16 Mar 2011, 17:23 | |
| - Dijkschneier a écrit:
- J'attends le problème 79 puisqu'on se comprend...
Le problème 78 n'est pas trivial, mon cher. - M.Marjani a écrit:
- Voici un problème de plus et qui est intéressant.
Problème 80 :
Soit a,b,c et d des réels positives . Montrer que :
(*) (a^5-a²+3)(b^5-b²+3)(c^5-c²+3) >= (a+b+c)^3 .
(**) (a+b)^3 (b+c)^3 (c+d)^3 (d+a)^3 ≥ 16a^2b^2c^2d^2 (a+b+c+d)^4 La première inégalité est classique. La solution est dans le lien suivant: http://www.artofproblemsolving.com/Wiki/index.php/2004_USAMO_Problems/Problem_5. Bonne découverte. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 19 Mar 2011, 11:27 Sam 19 Mar 2011, 11:27 | |
| - Mehdi.O a écrit:
- Problème 78:
Soit ABC un triangle et h l'hauteur issue de A. On note x=<BAC
i) Montrez que AB+AC>= BC.cosx + 2h.sinx
ii) Montrez le cas d'égalité Pour la question i) on note d'abord M la projection orthogonal de A sur (BC) [AM=h] on sait que +AC.cos(x-\widehat{ACM})) alors +\frac{AM}{AB}sin(x))+AC.(\frac{MC}{AC}cos(x)+\frac{AM}{AC}sin(x)) ) et ainsi .cos(x)+2AM.sin(x) ) finalement +2h.sin(x) ) C.Q.F.D sauf erreur! | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 19 Mar 2011, 11:30 Sam 19 Mar 2011, 11:30 | |
| - Mehdi.O a écrit:
- Problème 78:
Soit ABC un triangle et h l'hauteur issue de A. On note x=<BAC
i) Montrez que AB+AC>= BC.cosx + 2h.sinx
ii) Montrez le cas d'égalité et pour ii) suffit de resoudre les deux equations =1) et =1) et en deduire le resultat qui est je crois ABC triangle equilateral sauf erreur amicalement 
Dernière édition par yasserito le Mar 22 Mar 2011, 22:32, édité 2 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 19 Mar 2011, 13:36 Sam 19 Mar 2011, 13:36 | |
| | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 19 Mar 2011, 13:42 Sam 19 Mar 2011, 13:42 | |
| oui car en resolvant les deux equation on recoit x=ABM et x=ACM alors ABM=ACM
!que ce triangle soit isocele n'est pas suffisant ?? | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 19 Mar 2011, 13:48 Sam 19 Mar 2011, 13:48 | |
| - yasserito a écrit:
- oui car en resolvant les deux equation on recoit x=ABM et x=ACM alors ABM=ACM
!que ce triangle soit isocele n'est pas suffisant ?? Non. Puisque ABM=ACM=x=BAC. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 19 Mar 2011, 13:52 Sam 19 Mar 2011, 13:52 | |
| - mizmaz a écrit:
- yasserito a écrit:
- oui car en resolvant les deux equation on recoit x=ABM et x=ACM alors ABM=ACM
!que ce triangle soit isocele n'est pas suffisant ?? Non. Puisque ABM=ACM=x=BAC. Ae! dsl j'ai mal lu l'énoncé j'ai cru que x est inférieur ou égale a BAC.C'est rectifié Merci pour la clarification 
Dernière édition par yasserito le Mar 22 Mar 2011, 22:34, édité 1 fois | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 19 Mar 2011, 13:58 Sam 19 Mar 2011, 13:58 | |
| - yasserito a écrit:
- mizmaz a écrit:
- yasserito a écrit:
- oui car en resolvant les deux equation on recoit x=ABM et x=ACM alors ABM=ACM
!que ce triangle soit isocele n'est pas suffisant ?? Non. Puisque ABM=ACM=x=BAC. pourquoi x=BAC ??dsl si c'etait une question stupide de ma part!je sais que le triangle est iquelaterale mais cmt le prouver??
Lis l'énoncé.  | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 19 Mar 2011, 14:26 Sam 19 Mar 2011, 14:26 | |
| je crois que j'ai pas compris le signe est ce que le signe x=<BAC veut dire que x est inferieure ou egale a BAC ou bien que x=BAC ??
Dernière édition par yasserito le Mar 22 Mar 2011, 22:35, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 19 Mar 2011, 14:47 Sam 19 Mar 2011, 14:47 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 21 Mar 2011, 18:12 Lun 21 Mar 2011, 18:12 | |
| @nmo : OUi c'est l'idée, s'il aurait une tentative par les participants ça serait bien sure du joli travail. On peut donner une solution bien meilleur à celui qui figure au site, je suis optimiste.  - Mehdi.O a écrit:
- Problème 79:
On considère un triangle ABC . Le demi cerlce de diamètre BC coupe les côtés AB et AC en D et E respectivement, soient F et G les projections ortogonales de D et E sur BC. Les droites EF et DG se coupent en M.
Montrez que les droites BC et AM sont perpediculaires
Il n'y a pas quelque chose de dure dans ce problème. Par exemple, on peut tracer les deux triangles BDC et BEC qui sont rectangles, puis chercher deux triangles semblables affin d'appliquer Thalès et avoir soit (EG) // (AH) tel que H le projeté orthogonale de A sur [BC] cela si nous travaillons sur BEC. Je préfère d'utiliser AHC et EGC qui est facile de les prouvé semblables. . Un peu de trigonométrie, de calcules d'angles et trouver la relation entre les angles en les exprimant par les cotés des triangles permet de mettre fin à la démonstration. Désolé de passer très vite, c'est l'idée en principe. On peut attendre une solution bien détaillé, si j'avais du temps en ce moment je l'aurait déjà fait. PS : La question (ii) du dernier problème restant n'est qu'une histoire de chercher les théorèmes d'inégalités qui peuvent être interessant pour le résoudre. Cherchant un peu. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 | |
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 22 Mar 2011, 22:24 Mar 22 Mar 2011, 22:24 | |
| - Mehdi.O a écrit:
- M.Marjani a écrit:
- @nmo : OUi c'est l'idée, s'il aurait une tentative par les participants ça serait bien sure du joli travail. On peut donner une solution bien meilleur à celui qui figure au site, je suis optimiste.

- Mehdi.O a écrit:
- Problème 79:
On considère un triangle ABC . Le demi cerlce de diamètre BC coupe les côtés AB et AC en D et E respectivement, soient F et G les projections ortogonales de D et E sur BC. Les droites EF et DG se coupent en M.
Montrez que les droites BC et AM sont perpediculaires
Il n'y a pas quelque chose de dure dans ce problème. Par exemple, on peut tracer les deux triangles BDC et BEC qui sont rectangles, puis chercher deux triangles semblables affin d'appliquer Thalès et avoir soit (EG) // (AH) tel que H le projeté orthogonale de A sur [BC] cela si nous travaillons sur BEC. Je préfère d'utiliser AHC et EGC qui est facile de les prouvé semblables. .
Un peu de trigonométrie, de calcules d'angles et trouver la relation entre les angles en les exprimant par les cotés des triangles permet de mettre fin à la démonstration.
Désolé de passer très vite, c'est l'idée en principe. On peut attendre une solution bien détaillé, si j'avais du temps en ce moment je l'aurait déjà fait.
PS : La question (ii) du dernier problème restant n'est qu'une histoire de chercher les théorèmes d'inégalités qui peuvent être interessant pour le résoudre. Cherchant un peu.
Merci de donner des solution claires et nettes 
sinon une solution existe en utlisant soit CEVA soit Menelaus  Il ne s'agit pas d'une solution, il s'agit plutôt d'une indication puisque je n'ai pas cité Solution 79. VOilà c'est mieux que rien. .  Je présenterai une solution pour la question (ii) du problème 80 si personne n'a pu posté une solution juste jusqu'à la semaine prochaine. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 27 Mar 2011, 17:51 Dim 27 Mar 2011, 17:51 | |
| Cela fait 2 semaines qu'aucune solution n'a été posté au problème 79: Solution au problème 79 : Notons H le projeté orthogonal de A sur [BC], nous avons : ,A&space;\in&space;(BD),H\in&space;(BG)) ainsi il suffit de montrer par le théorème de Ménelaus dans le triangle 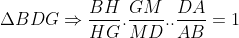 Puisque D et E appartiennet au cercle de diamètre [BC] donc: 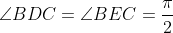 Donc: .sin(B)\wedge&space;EG=BC.cos(C).sin(C)) Et comme \left&space;|&space;\right&space;|(EG)) , il vient d'après Thalès que : .sin(C)}{cos(B).sin(B)}=\frac{cos(B).AB}{cos(C).AC}) Et nous avons aussi : \wedge&space;HG=AE.cos(C)\Rightarrow&space;\frac{BH}{HG}=\frac{AB.cos(B)}{AE.cos(C)}=\frac{AC.cos(B)}{AD.cos(C)}) car les deux triangles ) Ainsi 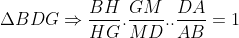 Et d'après le théorème de Ménelaus les points A,M,H sont allignés et ainsi (AM)et (BC) sont perpendiculaires. Et que chacun se sente libre de proposer un problème. P.S: @M.Marjani , il est temps que tu postes une solution à l'inégalité (ii) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 27 Mar 2011, 19:34 Dim 27 Mar 2011, 19:34 | |
| - M.Marjani a écrit:
- Problème 80 :
Soit a,b,c et d des réels positives . Montrer que :
(*) (a^5-a²+3)(b^5-b²+3)(c^5-c²+3) >= (a+b+c)^3 .
(**) (a+b)^3 (b+c)^3 (c+d)^3 (d+a)^3 ≥ 16a^2b^2c^2d^2 (a+b+c+d)^4 Je réponds: Je m'appuie sur la remarque suivante: (b+c)(c+d)(d+a)\ge (a+b+c+d)(abc+bcd+cda+dab)) . Démontrons ce lemme, on a: (b+c)(c+d)(d+a)&=(a+b)(c+d)(b+c)(d+a)\\&=(ac+ad+bc+bd)(bd+ba+cd+ca)\\&=(ac+bd)^2+(ad+bc)(cd+ba)+(ac+bd)(ad+bc+cd+ba)\\&=(ac+bd)^2+ad.cd+ad.ba+bc.cd+bc.ba+ac.ad+ac.bc+ac.cd+ac.ba+bd.ad+bd.bc+bd.cd+bd.ba\\&=(ac+bd)^2+d^2.ac+a^2.bd+c^2.bd+b^2.ac+a^2.cd+c^2.ab+c^2.ad+a^2.cb+d^2.ab+b^2.cd+d^2.bc+b^2.ad\\&=(ac+bd)^2+a^2(bc+cd+db)+b^2(ac+cd+da)+c^2(ab+bd+da)+d^2(ab+bc+ca)\\&\ge4abcd+a^2(bc+cd+db)+b^2(ac+cd+da)+c^2(ab+bd+da)+d^2(ab+bc+ca)\\&=abcd+a(abc+acd+adb)+abcd+b(bac+bcd+bda)+abcd+c(cab+cbd+cda)+abcd+d(dab+dbc+dca)\\&=a(bcd+abc+acd+adb)+b(acd+bac+bcd+bda)+c(abd+cab+cbd+cda)+d(abc+dab+dbc+dca)\\&=(a+b+c+d)(bcd+abc+acd+adb)\end{align*}) . (On a utilisé le fait que ^2\ge4abcd) selon l'inégalité arithmético-géométrique). On vient de démontrer que (b+c)(c+d)(d+a)\ge (a+b+c+d)(abc+bcd+cda+dab)) . Soit ^3(b+c)^3(c+d)^3(d+a)^3\ge (a+b+c+d)^3(abc+bcd+cda+dab)^3) .==>(1) D'autre part, on utilise l'inégalité de Maclaurin. Miracle, ce que je veux est le cas n=4, que Wikipédia lui présente une démonstration. Donc si x, y, z, et t sont des rééls strictement positifs, on aura ^{\frac{1}{3}}) . Revenons au problème en prenant: x=abc, y=bcd, z=cda, et t=dab, on trouve: ^{\frac{1}{3}}&\Leftrightarrow \big(\frac{abc+bcd+cda+dab}{4}\big)^3\ge\frac{a^2b^2c^2d^2.c+a^2b^2c^2d^2.d+a^2b^2c^2d^2.a+a^2b^2c^2d^2.d}{4}\\&\Leftrightarrow\frac{(abc+bcd+cda+dab)^3}{64}\ge\frac{a^2b^2c^2d^2.(a+b+c+d)}{4}\\&\Leftrightarrow(abc+bcd+cda+dab)^3\ge16a^2b^2c^2d^2.(a+b+c+d)\end{align}) . On vient de démontrer donc que ^3\ge16a^2b^2c^2d^2.(a+b+c+d)) .==>(2) En multipliant 1 et 2 membre par membre, on trouve ^3.(a+b)^3.(b+c)^3.(c+d)^3.(d+a)^3\ge16a^2b^2c^2d^2.(a+b+c+d)(a+b+c+d)^3.(abc+bcd+cda+dab)^3) . Ou encore ^3.(b+c)^3.(c+d)^3.(d+a)^3\ge16a^2b^2c^2d^2.(a+b+c+d)^4) . CQFD. Sauf erreur. P.S: A vous de chercher le cas d'égalité, car je commence à avoir le vertige en effectuant ces calculs. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 27 Mar 2011, 19:57 Dim 27 Mar 2011, 19:57 | |
| N'publiez pas qu'il nous reste le cas d'égalité pour l'exercice précédant. Je prends l'initiative et je vous propose l'exercice suivant, même s'il n'est pas trop difficile: Problème 81:Le plan est muni d'un repère orthonormé - ) . Trouvez une équation du cercle (C) dans les deux as suivants: 1- ) est son centre, et elle limite avec la droite :2x-5y+18=0) une corde dont la mesure est 6. 2-La droite :2x+y-5=0) est tangente au cercle en ) et la droite :2x+y+15) est aussi tangente au cercle. Bonne chance. | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 27 Mar 2011, 22:08 Dim 27 Mar 2011, 22:08 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 28 Mar 2011, 21:27 Lun 28 Mar 2011, 21:27 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Problème 80 :
Soit a,b,c et d des réels positives . Montrer que :
(*) (a^5-a²+3)(b^5-b²+3)(c^5-c²+3) >= (a+b+c)^3 .
(**) (a+b)^3 (b+c)^3 (c+d)^3 (d+a)^3 ≥ 16a^2b^2c^2d^2 (a+b+c+d)^4 Je réponds:
Je m'appuie sur la remarque suivante: (b+c)(c+d)(d+a)\ge (a+b+c+d)(abc+bcd+cda+dab)) . .
Démontrons ce lemme, on a:
(b+c)(c+d)(d+a)&=(a+b)(c+d)(b+c)(d+a)\\&=(ac+ad+bc+bd)(bd+ba+cd+ca)\\&=(ac+bd)^2+(ad+bc)(cd+ba)+(ac+bd)(ad+bc+cd+ba)\\&=(ac+bd)^2+ad.cd+ad.ba+bc.cd+bc.ba+ac.ad+ac.bc+ac.cd+ac.ba+bd.ad+bd.bc+bd.cd+bd.ba\\&=(ac+bd)^2+d^2.ac+a^2.bd+c^2.bd+b^2.ac+a^2.cd+c^2.ab+c^2.ad+a^2.cb+d^2.ab+b^2.cd+d^2.bc+b^2.ad\\&=(ac+bd)^2+a^2(bc+cd+db)+b^2(ac+cd+da)+c^2(ab+bd+da)+d^2(ab+bc+ca)\\&\ge4abcd+a^2(bc+cd+db)+b^2(ac+cd+da)+c^2(ab+bd+da)+d^2(ab+bc+ca)\\&=abcd+a(abc+acd+adb)+abcd+b(bac+bcd+bda)+abcd+c(cab+cbd+cda)+abcd+d(dab+dbc+dca)\\&=a(bcd+abc+acd+adb)+b(acd+bac+bcd+bda)+c(abd+cab+cbd+cda)+d(abc+dab+dbc+dca)\\&=(a+b+c+d)(bcd+abc+acd+adb)\end{align*}) . .
(On a utilisé le fait que ^2\ge4abcd) selon l'inégalité arithmético-géométrique). selon l'inégalité arithmético-géométrique).
On vient de démontrer que (b+c)(c+d)(d+a)\ge (a+b+c+d)(abc+bcd+cda+dab)) . .
Soit ^3(b+c)^3(c+d)^3(d+a)^3\ge (a+b+c+d)^3(abc+bcd+cda+dab)^3) .==>(1) .==>(1)
D'autre part, on utilise l'inégalité de Maclaurin.
Miracle, ce que je veux est le cas n=4, que Wikipédia lui présente une démonstration.
Donc si x, y, z, et t sont des rééls strictement positifs, on aura ^{\frac{1}{3}}) . .
Revenons au problème en prenant: x=abc, y=bcd, z=cda, et t=dab, on trouve:
^{\frac{1}{3}}&\Leftrightarrow \big(\frac{abc+bcd+cda+dab}{4}\big)^3\ge\frac{a^2b^2c^2d^2.c+a^2b^2c^2d^2.d+a^2b^2c^2d^2.a+a^2b^2c^2d^2.d}{4}\\&\Leftrightarrow\frac{(abc+bcd+cda+dab)^3}{64}\ge\frac{a^2b^2c^2d^2.(a+b+c+d)}{4}\\&\Leftrightarrow(abc+bcd+cda+dab)^3\ge16a^2b^2c^2d^2.(a+b+c+d)\end{align}) . .
On vient de démontrer donc que ^3\ge16a^2b^2c^2d^2.(a+b+c+d)) .==>(2) .==>(2)
En multipliant 1 et 2 membre par membre, on trouve ^3.(a+b)^3.(b+c)^3.(c+d)^3.(d+a)^3\ge16a^2b^2c^2d^2.(a+b+c+d)(a+b+c+d)^3.(abc+bcd+cda+dab)^3) . .
Ou encore ^3.(b+c)^3.(c+d)^3.(d+a)^3\ge16a^2b^2c^2d^2.(a+b+c+d)^4) . .
CQFD.
Sauf erreur.
P.S: A vous de chercher le cas d'égalité, car je commence à avoir le vertige en effectuant ces calculs. Trés bien ! Une belle solution. Le cas d'égalité n'est pas nécessaire. | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 29 Mar 2011, 10:30 Mar 29 Mar 2011, 10:30 | |
| Problème 82:Soit a,b,c des réels strictement positifs: Montrez que si:  On a :  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
