| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 13 Jan 2011, 20:21 Jeu 13 Jan 2011, 20:21 | |
| je voudrais une confirmation de ma reponse svp! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 14 Jan 2011, 12:49 Ven 14 Jan 2011, 12:49 | |
| - yasserito a écrit:
- je voudrais une confirmation de ma reponse svp!
La methode est bonne, mais le résultat est érroné. Tu as commis une faute nette dès le départ: - yasserito a écrit:
- selon la loi des sinus on a : sin(c)/n=sin(2c)/(n+2)=sin(TT-3c)/(n+1)
Tu as posé: 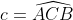 . Tu dois donc mettre 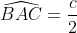 . A toi de rectifier ta solution. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 14 Jan 2011, 14:00 Ven 14 Jan 2011, 14:00 | |
| c'est rectifie mais il y'a une erreur je pense nn? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 15 Jan 2011, 18:55 Sam 15 Jan 2011, 18:55 | |
| - yasserito a écrit:
- svp ou est l'erreur?
L'erreur est dans l'énoncé. Désolé, j'ai mal recopié l'énoncé. Maintenant, c'est édité. Si tu as réctifié la solution, et tu as trouvé que n=4 (solution unique), tu peux proposer un nouvel exercice. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 15 Jan 2011, 19:37 Sam 15 Jan 2011, 19:37 | |
| | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 15 Jan 2011, 19:53 Sam 15 Jan 2011, 19:53 | |
| Probleme 46:
Soit x et y et z trois nombres appartenant a IR en tant que x+y+z=2
Prouvez que (x-2)²+(y-2)²+(z-2)²>=16/3 | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 15 Jan 2011, 20:57 Sam 15 Jan 2011, 20:57 | |
| - yasserito a écrit:
- Probleme 46:
Soit x et y et z trois nombres appartenant a IR en tant que x+y+z=2
Prouvez que (x-2)²+(y-2)²+(z-2)²>=16/3 - Spoiler:
Trivial.
1ère Méthode:la fonction f:x|-->(x-2)² est convexe sur R avec l'inégalité de Jensen on obtient f(x)+f(y)+f(z)>=3f((x+y+z)/3)=16/3
2ème méthode :
Avec C.S: 3((x-2)²+(y-2)²+(z-2)²)>=(x+y+z-6)² ce qui donne immédiatement l'inégalité désirée .
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 16 Jan 2011, 16:06 Dim 16 Jan 2011, 16:06 | |
| Sans perte de temps, voici un nouveau problème qui n'est pas facile: Problème 47:Démontrez que si on a ):|ax^2+bx+c|\le 1) , alors ):|cx^2+bx+a|\le 2) . Bonne chance.P.S: Remarquez la différence entre cet énoncé et celui de l'exercice 6 du livre de l'analyse (page 228)!!!
Dernière édition par nmo le Ven 28 Jan 2011, 12:11, édité 1 fois (Raison : Corriger le Latex) | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 19 Jan 2011, 19:04 Mer 19 Jan 2011, 19:04 | |
| [quote="nmo"] - Dijkschneier a écrit:
- Problème 17 :
Soit ABC un triangle et D le pied de la bissectrice intérieure de l'angle A.
Montrez que : AD² = AB.AC - BD.CD. Selon le théorèmer des bissectrices intérieures, on a ^2\bigg)) . ==>(1) Cette relation elle existe?? ou bien c'est un resultat de la relation principale de la bissectrice?? merci d'avance!^^ | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 20 Jan 2011, 15:28 Jeu 20 Jan 2011, 15:28 | |
| - yasserito a écrit:
- nmo a écrit:
- Dijkschneier a écrit:
- Problème 17 :
Soit ABC un triangle et D le pied de la bissectrice intérieure de l'angle A.
Montrez que : AD² = AB.AC - BD.CD. Selon le théorèmer des bissectrices intérieures, on a ^2\bigg)) . ==>(1) . ==>(1)
Cette relation elle existe?? ou bien c'est un resultat de la relation principale de la bissectrice?? merci d'avance!^^ Voilà le lien pour la solution: https://mathsmaroc.jeun.fr/seconde-tronc-commun-f6/bissectrice-d-un-angle-t13210.htm. Bonne découverte. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 20 Jan 2011, 20:21 Jeu 20 Jan 2011, 20:21 | |
| ah oui merci bcp!!mais est t'elle une relation directe qu'on peut utiliser directement sans la prouver svp? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 20 Jan 2011, 20:45 Jeu 20 Jan 2011, 20:45 | |
| - yasserito a écrit:
- ah oui merci bcp!!mais est t'elle une relation directe qu'on peut utiliser directement sans la prouver svp?
Non. Pas très très connue. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 23 Jan 2011, 17:19 Dim 23 Jan 2011, 17:19 | |
| - nmo a écrit:
- Sans perte de temps, voici un nouveau problème qui n'est pas facile:
Problème 47:
Démontrez que si on a ):|ax^2+bx+c|\le 1) , alors , alors ):|cx^2+bx+a|\le 2) . .
Bonne chance.
P.S: Remarquez la différence entre cet énoncé et celui de l'exercice 6 du livre de l'analyse (page 228)!!! Ainsi, je suis obligé à proposer une solution, le voici: On a ):|ax^2+bx+c|\le 1) . On prend x=1, on trouve que 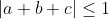 .==>(1) (Donc 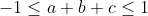 .) On prend x=-1, on trouve que 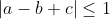 .==>(2) (Donc 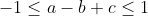 .) On prend x=0, on trouve que 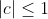 .==>(3) Et on a ):|cx^2+bx+a|=|cx^2-c+a+bx+c|) . Et selon l'inégalité trigonométrique, il vient que ):|cx^2-c+a+bx+c|\le |cx^2-c|+|a+bx+c|) . Donc ):|cx^2+bx+a|\le |c||x^2-1|+|a+bx+c|) .==>(*) On passe dorénavant au travail sérieux: D'un premier côté: On pose: ): f(|c|)=|c||x^2-1|) . Et puisque ): -1\le x\le1) . Alors ): x^2\le1) . Donc ): x^2-1\le0) . Donc ): |x^2-1|=1-x^2) . Soit à écrire ): f(|c|)=(1-x^2)|c|) . Donc f est une fonction linéaire, dont le coefficient est positif. Elle est donc croissante pour tout |c| de [0,1]. Selon 3, on a 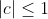 . Donc \le f(1)) . Donc ): (1-x^2)|c|\le (1-x^2)*|1|) . Donc ): (1-x^2)|c|\le 1-x^2) . Et on a ): 0\le x^2\le 1) . Donc ): -1\le -x^2\le 0) . Donc ): 1-x^2\le 1) . On déduit que ): (1-x^2)|c|\le 1) .==>(a) D'un second côté: On pose =a+bx+c) . (g est une fonction affine, dont le coefficient est b et de terme constant a+c) -Si b est positif, la fonction g sera croissante pour tout x de [-1,1]. On a ):-1\le x\le 1) . Donc ): g(-1)\le g(x)\le g(1)) . Donc ): a-b+c\le g(x)\le a+b+c) . Selon 1 et 2, il vient que ): -1\le g(x)\le 1) . Donc ): |g(x)|\le 1) . -Si b est négatif, la fonction g sera décroissante pour tout x de [-1,1]. On a ): -1\le x\le 1) . Donc ):g(1)\le g(x)\le g(-1)) . Donc ): a+b+c\le g(x)\le a-b+c) . Selon 1 et 2, il vient que ): -1\le g(x)\le 1) . Donc ): |g(x)|\le 1) . Dans tous les cas, on a ):|a+bx+c|\le 1) .==>(b) De a et b ,on conclût que ):|cx^2+bx+a|\le 1+1) . Soit ):|cx^2+bx+a|\le 2) . CQFD. Sauf erreur.
Dernière édition par nmo le Ven 28 Jan 2011, 12:09, édité 1 fois (Raison : Corriger le Latex) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 23 Jan 2011, 17:38 Dim 23 Jan 2011, 17:38 | |
| Cette fois-ci, je n'ai pas de problème à proposer.
Que quelqu'un se sente libre pour le faire.
P.S: J'attends une confirmation pour ma solution précédante. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 23 Jan 2011, 17:46 Dim 23 Jan 2011, 17:46 | |
| Ta solution précédente est tout à fait juste.
Je m'attendais à ce que tu postes un nouveau problème, et j'aimerais que tu le fasses, car je n'ai pas non plus un problème approprié à proposer. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 23 Jan 2011, 18:07 Dim 23 Jan 2011, 18:07 | |
| Voici un exercice que je n'ai pas encore résolu: Problème 48:Soit a et b deux réels. Démontrez que =\frac{a+b-|a-b|}{2}) . Démontrez que =\frac{a+b+|a-b|}{2}) . Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 23 Jan 2011, 19:00 Dim 23 Jan 2011, 19:00 | |
| Disjonction de cas : si a>=b, et si a<b.
J'attends le problème 49. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 23 Jan 2011, 19:42 Dim 23 Jan 2011, 19:42 | |
| - Dijkschneier a écrit:
- Disjonction de cas : si a>=b, et si a<b.
J'attends le problème 49. Tu peux détailler, monsieur. Voici un problème tiré du manuel: Problème 49:Soit _{n\in\mathbb_{N}}) définie par  . Trouvez 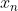 en fonction de n. Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 24 Jan 2011, 15:52 Lun 24 Jan 2011, 15:52 | |
| Puisqu'on est en vacance, je vous attends jusqu'à demain et je donne ma réponse.
Un petit indice: comptez combien de 2 a-t-on dans chaque nombre calculé. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 24 Jan 2011, 16:07 Lun 24 Jan 2011, 16:07 | |
| Solution au problème 49 :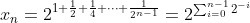 Et on peut le prouver par récurrence forte... Singularité : la limite de cette suite vaut 4. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 24 Jan 2011, 16:28 Lun 24 Jan 2011, 16:28 | |
| - Dijkschneier a écrit:
- Solution au problème 49 :
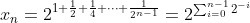
Et on peut le prouver par récurrence forte...
Singularité : la limite de cette suite vaut 4. J'attends une solution détaillée de ta part, et je vais donner la mienne après un instant. Je veux savoir comment tu vas calculer 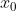 . | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 24 Jan 2011, 18:43 Lun 24 Jan 2011, 18:43 | |
| x0 déroge en effet à la formule : il faut faire de x0 un cas spécial en disant conjointement à la formule que j'ai énoncée que x0 = 1.
Si c'est à moi de proposer un nouveau problème, je propose :
Problème 50 : (** : deux étoiles)
Trouver toutes les fonctions f : Z -> Z telles que :
f(x-y+f(y)) = f(x) + f(y) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 24 Jan 2011, 19:10 Lun 24 Jan 2011, 19:10 | |
| - nmo a écrit:
- Problème 49:
Soit _{n\in\mathbb_{N}}) définie par définie par  . .
Trouvez 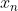 en fonction de n. en fonction de n.
Bonne chance. Voici ma solution basé sur le principe de récurrence: *On démontre que : x_{n+1}=2\sqrt{x_n}) . -On vérifie la relation pour l'indice 0. On a 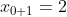 et 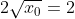 . Donc 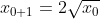 . La propriété est donc vraie pour n=0. -On démontre l'héridité: Supposons que la propriété est vraie au rang n, et démontrons qu'elle l'est aussi à l'indice n+1. C'est à dire, démontrons que 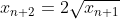 . (N'oublions pas que 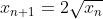 ). On a selon les données, 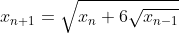 . On effectue la transformation: changer n par n+1. On trouve 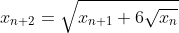 . Donc 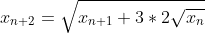 . Donc 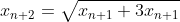 . Donc 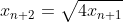 . Donc 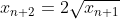 . La propriété est donc vraie pour l'indice n+1. -Sythèse du principe de la récurrence: On a : x_{n+1}=2\sqrt{x_n}) .==>(1) *On démontre que \in\mathbb{N}^2): x_{n+k}=2^{(\frac{2^k-1}{2^{k-1}})}.x_n^{2^{(-k)}}) . La récurrence se fait sur k. -On démontre la relation pour l'indice 0. On a }.x_n^{2^{(-0)}}=2^{(\frac{1-1}{2^{0-1}})}.x_n^{2^(-0)}) . Donc }.x_n^{2^{(-0)}}=2^{(\frac{0}{2^{0-1}})}.x_n^{2^0}) . Donc }.x_n^{2^{(-0)}}=2^{0}.x_n^{1}) . Donc }.x_n^{2^{(-0)}}=1.x_n) . Donc }.x_n^{2^{(-0)}}=x_{n+0}) . La propriété est donc vraie pour n=0. -On démontre l'héridité: Supposons que la propriété est vraie au rang n, et démontrons qu'elle l'est aussi à l'indice n+1. C'est à dire, démontrons que }.x_n^{2^{(-k-1)}}) . (N'oublions pas que }.x_n^{2^{(-k)}}) ). On a 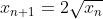 . On effectue la transformation: changer n par n+k. On trouve 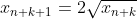 . Donc }.x_n^{2^{(-k)}}}) . Donc *\frac{1}{2}}.x_n^{2^{(-k)}*\frac{1}{2}}}) . Donc }.x_n^{2^{(-k)}*2^{(-1)}}}) . Donc }.x_n^{2^{(-k-1)}}}}) . Donc }.x_n^{2^{(-k-1)}}}}) . Donc }.x_n^{2^{(-k-1)}}}}) . Donc }.x_n^{2^{(-k-1)}}}}) . La propriété est donc vraie pour l'indice k+1. -Sythèse du principe de la récurrence: On a \in\mathbb{N}^2): x_{n+k}=2^{(\frac{2^k-1}{2^{k-1}})}.x_n^{2^{(-k)}}) .==>(2) *Conclusion: On prend n=0 dans la formule 2, on trouve que : x_{0+k}=2^{(\frac{2^k-1}{2^{k-1}})}.x_0^{2^{(-k)}}) . Donc : x_{k}=2^{(\frac{2^k-1}{2^{k-1}})}*1^{2^{(-k)}}) . Donc : x_{k}=2^{(\frac{2^k-1}{2^{k-1}})}*1) . Soit finalement : x_{k}=2^{(\frac{2^k-1}{2^{k-1}})}) . Sauf erreur.
Dernière édition par nmo le Ven 28 Jan 2011, 11:57, édité 1 fois (Raison : Corriger le Latex) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 24 Jan 2011, 19:16 Lun 24 Jan 2011, 19:16 | |
| - Dijkschneier a écrit:
- x0 déroge en effet à la formule : il faut faire de x0 un cas spécial en disant conjointement à la formule que j'ai énoncée que x0 = 1.
Je sais la réponse ultérieurement, et je m'attendait à une réponse bonne autre que celle-là. En effet, il faut remarquer que la somme 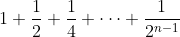 s'agit d'une somme des termes successifs d'une suite géométrique de raison 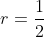 . On écrit 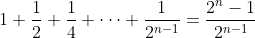 . Tu peux ainsi calculer aisément le premier terme de notre suite. Jette un coup d'oeuil sur ma solution. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 25 Jan 2011, 15:38 Mar 25 Jan 2011, 15:38 | |
| Solution 50:Soit f la fonction vérifiant les données, tel que )%20=%20f(x)%20+%20f(y).) En effectuant des changements sur l'EF du départ il s'ensuit : :%20f(f(x))%20=%202f(x)) . De méme :%20f(f(x)-x)%20=%20f(x)%20+%20f(0)) Soit en posant =c/c\in%20\mathbb{Z}) on écrit %20=%20f(f(x)-x)%20=%202(f(x)-x)%20\Rightarrow) =2x+c) Si Si 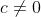 : : f(f(0))=2f(0) donc f(f(0)) est différent de zéro, et à chaque fois qu'on donne à x=y la valeur f(0) dans l'E.F du départ on déduira que \neq%200) / 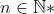 (façile à démontrer par une réccurence immédiate). Mais =0) vérifie bien l'énoncé. Ce qui est clairement absurde. Donc =0) Réciproquement, les deux fonctions =2x\textup{\mathrm{%20Et%20}}f(x)=0) réalisent l'equation fonctionelle ainsi les donées. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
