| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 25 Jan 2011, 16:13 Mar 25 Jan 2011, 16:13 | |
| - M.Marjani a écrit:
- De méme
:f(f(x)-x)=f(x)+f(0)) C'est faux, ce que tu écris. Lorqu'on remplace y par 0 et on laisse x tel qu'il est, l'équation fonctionnelle s'écrit f(x+f(0))=f(x)+f(0). Il faut penser à rectifier. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 25 Jan 2011, 16:39 Mar 25 Jan 2011, 16:39 | |
| - nmo a écrit:
- M.Marjani a écrit:
- De méme
:f(f(x)-x)=f(x)+f(0)) C'est faux, ce que tu écris.
Lorqu'on remplace y par 0 et on laisse x tel qu'il est, l'équation fonctionnelle s'écrit f(x+f(0))=f(x)+f(0).
Il faut penser à rectifier. Normalement c'est f(y,0) mais y peut étre remplacer par n'importe quel variable appartenant à IZ, on a choisi x par exemple : ) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 25 Jan 2011, 17:03 Mar 25 Jan 2011, 17:03 | |
| Il y a encore un problème ici : %20=%20f(f(x)-x)%20=%202(f(x)-x)%20\Rightarrow) On a f(f(x))=2f(x), pas f(f(x)-x)=2(f(x)-x). | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 25 Jan 2011, 17:08 Mar 25 Jan 2011, 17:08 | |
| - M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- De méme
:f(f(x)-x)=f(x)+f(0)) C'est faux, ce que tu écris.
Lorqu'on remplace y par 0 et on laisse x tel qu'il est, l'équation fonctionnelle s'écrit f(x+f(0))=f(x)+f(0).
Il faut penser à rectifier. Normalement c'est f(y,0) mais y peut étre remplacer par n'importe quel variable appartenant à IZ, on a choisi x par exemple : ) Oui, je trouve que tu as pris x=0, pour atteindre f(-y+f(y))=f(y)+f(0). Puis tu as pris x=y pour avoir le résultat que tu as déjà avancé. - M.Marjani a écrit:
- Soit en posant
=c/c\in%20\mathbb{Z}) on écrit on écrit -x)%20=%202(f(x)-x)) Personnellement, cela est visiblement faux, tu mets f(x)-x à la place de f(x) comme si f(x) était la variable.
Dernière édition par nmo le Mar 25 Jan 2011, 17:09, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 25 Jan 2011, 17:09 Mar 25 Jan 2011, 17:09 | |
| - Dijkschneier a écrit:
- Il y a encore un problème ici :
%20=%20f(f(x)-x)%20=%202(f(x)-x)%20\Rightarrow)
On a f(f(x))=2f(x), pas f(f(x)-x)=2(f(x)-x). Il ne manque que la surjection de f pour en déduire que f(x)=2x. [ puisqu'on a eu auparavant f(f(x))=2f(x)] . EDIT: Je vois qu'il suffit de montrer l'injection de f, puis sa surjection pour en déduire les solutions: c'est le but du probléme. Pour l'injection de f:Ce qui compte démontrer est ,f(y))\in%20\mathbb{Z}):f(f(x))=f(f(y))\Rightarrow%20f(x)=f(y)) Supposons que f(f(x))=f(f(y)) il reste donc à montrer le fait que f(x)=f(y): Puisqu'on a déjà montrer f(f(x))=2f(x) alors : f(f(x))=f(f(y)) <=> 2f(x)=2f(y) <=> f(x)=f(y) Donc f est injective.. Pour la surjection de f:(\exists%20f(x)\in%20\mathbb{Z}):f(f(x))=t\Leftrightarrow%202f(x)=t\Leftrightarrow%20f^{-1}(f(x))=f^{-1}(\frac{t}{2})) (On va utiliser l'injection de f) =f^{-1}(f(x)+f(y))=f^{-1}(f(x-y+f(y)))=x-y+f(y)=f(x)) puisqu'on a posé x=y. =\frac{t}{2}\Rightarrow%20f^{-1}(\frac{t}{2})=\frac{t}{4}) alors )=x=\frac{t}{4}) D'ou la surjectivité de f, ainsi f est une bijection donc =2x) est une solution, f(x)=0 est la deuxiéme solution. Réciproquement, les deux fonctions répondent au données. PS: Il existe une deuxiéme maniére de prouver la surjectivité de f, et peut-étre schematisé de la maniére suivante: f est une surjection <=> f(2x)=2f(x) ET l'unicité du x. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 26 Jan 2011, 17:08 Mer 26 Jan 2011, 17:08 | |
| - Dijkschneier a écrit:
- Problème 50 : (** : deux étoiles)
Trouver toutes les fonctions f : Z -> Z telles que :
f(x-y+f(y)) = f(x) + f(y) On traite deux cas, ou bien f est constante ou bien sinon. -Cas premier: f est constante. Donc, il existe un entier z tel que pour tout entier x on ait f(x)=z. Donc l'équation fonctionnellle s'écrit z=z+z. Donc z=0. Ainsi la fonction nulle est solution à l'équation fonctionnelle. -Cas second: f n'est pas constante. *Démontreons que f est injective: Fixons x=y, l'équation fonctionnelle s'écrit f(x-x+f(x))=f(x)+f(x). Donc f(f(x))=2f(x). Posons a=f(x) et b=f(y). Donc f(a)=2a et f(b)=2b. Supposons que f(a)=f(b). Donc 2a=2b. Donc a=b. Ainsi f est injective. *Calculons f(0): Fixons x=-f(0) et y=0, l'équation fonctionnelle s'écrit f(-f(0)-0+f(0))=f(-f(0))+f(0). Donc f(0)=f(-f(0))+f(0). Donc f(-f(0))=0.==>(1) Fixons x=-f(-f(0)) et y=-f(0), l'équation fonctionnelle s'écrit f(-f(-f(0))-(-f(0))+f(-f(0)))=f(-f(-f(0)))+f(-f(0)). Donc en utilisant 1, f(f(0))=f(-f(-f(0))). Donc en utilisant l'injectivité, f(0)=-f(-f(0)). Donc en utilisant 1, f(0)=0. *Cherchons les solutions: Fixons x=2y-f(y) et laissons y tel qu'il est, l'équation fonctionnelle s'écrit f(2y-f(y)-y+f(y))=f(2y-f(y))+f(y). Donc f(y)=f(2y-f(y))+f(y). Donc f(2y-f(y))=0. Donc f(2y-f(y))=f(0). Donc en utilisant l'injectivité 2y-f(y)=0. Donc f(y)=2y. *Réciproquemet, soit f la fonction définie par f(x)=2x. On a f(x-y+f(y))=f(x-y+2y). Donc f(x-y+f(y))=f(x+y). Donc f(x-y+f(y))=2(x+y). Donc f(x-y+f(y))=2x+2y. Et f(x)+f(y)=2x+2y. Donc f(x-y+f(y))=f(x)+f(y). Ainsi la fonction f définie par f(x)=2x est solution de l'équation. -Conclusion: Les deux fonctions solutions à l'équations sont x|->2x et la fonction nulle. Sauf erreur. P.S: J'attends une confirmation pour pouvoir continuer le jeu. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 26 Jan 2011, 17:25 Mer 26 Jan 2011, 17:25 | |
| Non.
Tu as fait des erreurs de raisonnement en voulant prouver l'injectivité. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 26 Jan 2011, 17:28 Mer 26 Jan 2011, 17:28 | |
| - Dijkschneier a écrit:
- Non.
Tu as fait des erreurs de raisonnement en voulant prouver l'injectivité. Où exactement? | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 26 Jan 2011, 17:29 Mer 26 Jan 2011, 17:29 | |
| - nmo a écrit:
- Dijkschneier a écrit:
- Problème 50 : (** : deux étoiles)
Trouver toutes les fonctions f : Z -> Z telles que :
f(x-y+f(y)) = f(x) + f(y) On traite deux cas, ou bien f est constante ou bien sinon.
-Cas premier: f est constante.
Donc, il existe un entier z tel que pour tout entier x on ait f(x)=z.
Donc l'équation fonctionnellle s'écrit z=z+z.
Donc z=0.
Ainsi la fonction nulle est solution à l'équation fonctionnelle.
-Cas second: f n'est pas constante.
*Démontreons que f est injective:
Fixons x=y, l'équation fonctionnelle s'écrit f(x-x+f(x))=f(x)+f(x).
Donc f(f(x))=2f(x).
Posons a=f(x) et b=f(y).Donc f(a)=2a et f(b)=2b.
Supposons que f(a)=f(b).
Donc 2a=2b.
Donc a=b.
Ainsi f est injective.
*Calculons f(0):
Fixons x=-f(0) et y=0, l'équation fonctionnelle s'écrit f(-f(0)-0+f(0))=f(-f(0))+f(0).
Donc f(0)=f(-f(0))+f(0).
Donc f(-f(0))=0.==>(1)
Fixons x=-f(-f(0)) et y=-f(0), l'équation fonctionnelle s'écrit f(-f(-f(0))-(-f(0))+f(-f(0)))=f(-f(-f(0)))+f(-f(0)).
Donc en utilisant 1, f(f(0))=f(-f(-f(0))).
Donc en utilisant l'injectivité, f(0)=-f(-f(0)).
Donc en utilisant 1, f(0)=0.
*Cherchons les solutions:
Fixons x=2y-f(y) et laissons y tel qu'il est, l'équation fonctionnelle s'écrit f(2y-f(y)-y+f(y))=f(2y-f(y))+f(y).
Donc f(y)=f(2y-f(y))+f(y).
Donc f(2y-f(y))=0.
Donc f(2y-f(y))=f(0).
Donc en utilisant l'injectivité 2y-f(y)=0.
Donc f(y)=2y.
*Réciproquemet, soit f la fonction définie par f(x)=2x.
On a f(x-y+f(y))=f(x-y+2y).
Donc f(x-y+f(y))=f(x+y).
Donc f(x-y+f(y))=2(x+y).
Donc f(x-y+f(y))=2x+2y.
Et f(x)+f(y)=2x+2y.
Donc f(x-y+f(y))=f(x)+f(y).
Ainsi la fonction f définie par f(x)=2x est solution de l'équation.
-Conclusion:
Les deux fonctions solutions à l'équations sont x|->2x et la fonction nulle.
Sauf erreur.
P.S: J'attends une confirmation pour pouvoir continuer le jeu. Tu n'as pas le droit de poser f(x)=a , t'as besoin de la surjectiveté de f :d - Spoiler:
Qui peut vous garantir que se sont les seules solutions non autres?
Dernière édition par M.Marjani le Mer 26 Jan 2011, 17:37, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 26 Jan 2011, 17:33 Mer 26 Jan 2011, 17:33 | |
| - M.Marjani a écrit:
- Tu n'as pas le droit de poser f(x)=a , t'as besoin de la surjectiveté de f :d
Je ne veux par cela que simplifier mes calculs, pas autre chose. En plus, je ne sais pas pourquoi j'ai besoin de la surjectivité? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 26 Jan 2011, 17:42 Mer 26 Jan 2011, 17:42 | |
| Pour prouver l'injectivité, tu choisis deux réels a et b arbitraires, on est d'accord ?
Comment tu prouves alors que a=b ?
Si j'ai bien compris ce que tu fais, tu pose a=f(x) et b=f(y) et donc f(a)=f(f(x))=2f(x)=2a et f(b)=f(f(y))=2f(y)=2b.
Mais tu ne peux pas faire cette substitution, car comme Marjani l'a souligné, tu as besoin de la surjectivité pour le faire. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 26 Jan 2011, 18:04 Mer 26 Jan 2011, 18:04 | |
| - Dijkschneier a écrit:
- Pour prouver l'injectivité, tu choisis deux réels a et b arbitraires, on est d'accord ?
Comment tu prouves alors que a=b ?
Si j'ai bien compris ce que tu fais, tu pose a=f(x) et b=f(y) et donc f(a)=f(f(x))=2f(x)=2a et f(b)=f(f(y))=2f(y)=2b.
Mais tu ne peux pas faire cette substitution, car comme Marjani l'a souligné, tu as besoin de la surjectivité pour le faire. Je ne vois pas comment "pourquoi je dois faire prouver la surjectivité" , qu'est-ce que tu penses si j'ai fait: - Citation :
- *Démontreons que f est injective:
Fixons x=y, l'équation fonctionnelle s'écrit f(x-x+f(x))=f(x)+f(x).
Donc f(f(x))=2f(x).
Supposons que f(f(x))=f(f(y)).
Donc 2f(x)=2f(y).
Donc f(x)=f(y).
Ainsi f est injective. Ce que j'ai fait est que simplifier mes calculs, tu vois? Pourquoi donc la surjectivité? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 14:57 Jeu 27 Jan 2011, 14:57 | |
| J'attends une confirmation, afin de continuer ou reprendre mon travail. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 15:02 Jeu 27 Jan 2011, 15:02 | |
| Ta démarche est fausse nmo, pour la raison que j'ai indiquée.
L'injectivité est difficile à prouver.
Signalez-le moi si je dois poster une solution afin que ce jeu ne s'arrête pas. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 15:09 Jeu 27 Jan 2011, 15:09 | |
| - Dijkschneier a écrit:
- Signalez-le moi si je dois poster une solution afin que ce jeu ne s'arrête pas.
Vas-y, tu peux proposer une solution. pour moi je renonce, je n'ai aucune autre idée qui peut me servir, j'ai silloné plusieurs chemins mais en vain. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 15:10 Jeu 27 Jan 2011, 15:10 | |
| Prière de poster une solution, pour le bon déroulement du jeu. Ca commence à ralentir surtout que cet exercice est posté depuis 4 jours, et qu'on est plein vaccances  Amicalement  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 15:17 Jeu 27 Jan 2011, 15:17 | |
| Vous pouvez trouver ma solution en bas de page ici : http://www.artofproblemsolving.com/Forum/viewtopic.php?f=38&t=149172&p=2154661#p2154661
Et que chacun se sente libre de proposer de nouveaux problèmes. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 15:42 Jeu 27 Jan 2011, 15:42 | |
| Je prends l'initiative:
Problème 51:
Soit f une fonction polynôme du second degré.
Démontrez que si l'équation f(x)=x n'admet pas de solutions en IR, alors l'équation f(f(x))=x l'est également.
Bonne chance.
Dernière édition par nmo le Ven 28 Jan 2011, 10:35, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 16:15 Jeu 27 Jan 2011, 16:15 | |
| Solution au problème 51 :
f est un pôlynome, et l'équation f(x)=x n'admet pas de solutions dans IR.
Donc f(x)>x ou f(x)<x
considérons la fonction g(x)=f(x)-x celle-ci est aussi polynôme, il s'ensuit que pour tout x € IR f(f(x))<f(x)<x ou f(f(x))>f(x)>x
Ainsi f(x)#x pour tout x € IR
Synthèse: l'équation ff(x))=x n'admet pas de solutions dans IR.
P.S: j'ai présente une solution de DIMA DIMA.
J'attends une confirmation pour pouvoir poster un nouveau problème. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 16:22 Jeu 27 Jan 2011, 16:22 | |
| - Dijkschneier a écrit:
- Vous pouvez trouver ma solution en bas de page ici : http://www.artofproblemsolving.com/Forum/viewtopic.php?f=38&t=149172&p=2154661#p2154661
Et que chacun se sente libre de proposer de nouveaux problèmes. Peux-tu m'éclairer la dernière ligne? - Mehdi.O a écrit:
- Solution au problème 51 :
f est un pôlynome, et l'équation f(x)=x n'admet pas de solutions dans IR.
Donc f(x)>x ou f(x)<x
considérons la fonction g(x)=f(x)-x celle-ci est aussi polynôme, il s'ensuit que pour tout x € IR f(f(x))<f(x)<x ou f(f(x))>f(x)>x Ainsi f(x)#x pour tout x € IR
Synthèse: l'équation ff(x))=x n'admet pas de solutions dans IR.
P.S: j'ai présente une solution de DIMA DIMA.
J'attends une confirmation pour pouvoir poster un nouveau problème. Je ne vois pas comment tu as abouti à une telle conclusion.
Dernière édition par nmo le Jeu 27 Jan 2011, 16:31, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 16:28 Jeu 27 Jan 2011, 16:28 | |
| Oui moi même je ne vois pas comment ils ont fait pour résulter à cela.
Voilà ils ont traité (à mon avis) la monotonie de f. Mais ils ont négligé deux cas :
si f(x)>x et f est strictement décroissante alors on a f(f(x))<f(x) et f(x)>x, ceci ne nous permet pas de conclure que f(f(x))>f(x)>x.
Bref, je vais essayer de chercher une autre solution propre à moi. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 17:54 Jeu 27 Jan 2011, 17:54 | |
|
Dernière édition par M.Marjani le Jeu 27 Jan 2011, 20:15, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 27 Jan 2011, 18:39 Jeu 27 Jan 2011, 18:39 | |
| La solution qu'a proposé Mehdi demande de connaître la notion de "continuité" pour être bien comprise.
f(x) étant une fonction polynomiale, g(x) = f(x)-x l'est aussi.
Or toute fonction polynomiale est continue.
S'il existait deux réels a et b tels que g(a)>0 et g(b)<0, alors d'après le théorème des valeurs intermédiaires, il existerait un réel c strictement compris entre a et b tel que g(c)=0. Ce qui serait bien sûr une contradiction.
Par conséquent, on a soit :
1) Pour tout réel x : g(x) > 0, ce qui est équivalent à : pour tout réel x : f(x) > x
2) Pour tout réel x : g(x) < 0, ce qui est équivalent à : pour tout réel x : f(x) < x
Il ne reste plus qu'à remplacer x par f(x) pour avoir soit :
1) f(f(x)) > f(x), ce qui implique que f(f(x))>x puisque f(x)>x
2) f(f(x)) < f(x), ce qui implique que f(f(x))<x puisque f(x)<x
En particulier, f(f(x)) n'est jamais égal à x.
Et ce qu'écrit M.Marjani est bien sûr faux puisqu'il fait des erreurs de logique...
Dernière édition par Dijkschneier le Ven 28 Jan 2011, 11:49, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 28 Jan 2011, 10:58 Ven 28 Jan 2011, 10:58 | |
| La solution que présente Dijkschneier est meilleure, sauf la légère faute de frappe vers la fin (au lieu de f(x)<x, il met f(x)<0). Je propose un exercice, tiré d'un olympiade algérien: Exercice 52:Démontrez que: :(a-2\sqrt{a}+2)^3\ge6\sqrt{a}-3a-2) . Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 28 Jan 2011, 11:46 Ven 28 Jan 2011, 11:46 | |
| Solution au problème 52 :On pose tout d'abord x=sqrt(a). Alors : LHS - RHS =  = 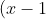^2%20(10%20-%2010%20x%20+%209%20x^2%20-%204%20x^3%20+%20x^4)) Or :  (IAG) Et :  (Delta...) Done !
Dernière édition par Dijkschneier le Sam 29 Jan 2011, 21:51, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
