| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 28 Jan 2011, 12:42 Ven 28 Jan 2011, 12:42 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 28 Jan 2011, 13:28 Ven 28 Jan 2011, 13:28 | |
| Problème 53:Soit ABCD un carré de côté 1. Soient deux points M et N de (AB) et (BC) respectivement, de telle sorte que  . Calculez le périmètre du triangle MNB. Bonne chance. | |
|
  | |
princessdesmaths
Maître

 Nombre de messages : 149 Nombre de messages : 149
Age : 29
Localisation : Casablanca
Date d'inscription : 24/09/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 28 Jan 2011, 18:57 Ven 28 Jan 2011, 18:57 | |
| se preparer au olympiades !!! pourquoi faire puiceque ce n'est que de la tricherie ?!! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 28 Jan 2011, 20:56 Ven 28 Jan 2011, 20:56 | |
| Je propose un autre exercice Problème 54:Démontrez que : E(\frac{n-1}{2})+E(\frac{n+2}{4})+E(\frac{n+4}{4})=n) . Où E(x) désige la partie entière de x. Bonne chance.P.S: Je vais voous présenter les solutios demain, et je crois qu'une nuit est suffisante pour traiter ces deux exercices. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 28 Jan 2011, 21:34 Ven 28 Jan 2011, 21:34 | |
| Solution au problème 54 :
L'idée encore une fois c'est d'effectuer la division euclidienne de n par 4 : n = 4k+r.
Le reste n'est qu'une étude de cas. | |
|
  | |
mayback
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 30
Date d'inscription : 21/05/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 00:21 Sam 29 Jan 2011, 00:21 | |
| Une petite question, c'est quoi lHS et RHS, et sinon est ce que qq peut m'expliquer IAG ?
Merci
Mayback | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 14:09 Sam 29 Jan 2011, 14:09 | |
| LHS = Left Hand Side partie gauche
RHS = Right Hand Side partie droite
IAG
http://www.animath.fr/IMG/pdf/cours-ineg.pdf
Page 15 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 16:05 Sam 29 Jan 2011, 16:05 | |
| - Dijkschneier a écrit:
- Solution au problème 54 :
L'idée encore une fois c'est d'effectuer la division euclidienne de n par 4 : n = 4k+r.
Le reste n'est qu'une étude de cas. J'avoue que c'est l'idée que j'avais en tête, je développe alors: Cas premier: n=4k. +E(\frac{n+2}{4})+E(\frac{n+4}{4})&=E(\frac{4k-1}{2})+E(\frac{4k+2}{4})+E(\frac{4k+4}{4})\\&=E(2k-\frac{1}{2})+E(k+\frac{1}{2})+E(k+1)\\&=2k+E(\frac{-1}{2})+k+E(\frac{1}{2})+k+1\\&=2k-1+k+0+k+1\\&=4k\\&=n\end{align*}) . Cas second: n=4k+1. +E(\frac{n+2}{4})+E(\frac{n+4}{4})&=E(\frac{4k+1-1}{2})+E(\frac{4k+1+2}{4})+E(\frac{4k+1+4}{4})\\&=E(2k+0)+E(k+\frac{3}{4})+E(k+\frac{5}{4})\\&=2k+k+E(\frac{3}{4})+k+E(\frac{5}{4})\\&=3k+0+k+1\\&=4k+1\\&=n\end{align*}) . Cas troisième: 4k+2 +E(\frac{n+2}{4})+E(\frac{n+4}{4})&=E(\frac{4k+2-1}{2})+E(\frac{4k+2+2}{4})+E(\frac{4k+2+4}{4})\\&=E(2k+\frac{1}{2})+E(k+1)+E(k+\frac{3}{2})\\&=2k+E(\frac{1}{2})+k+1+k+E(\frac{3}{2})\\&=2k+0+k+1+k+1\\&=4k+2\\&=n\end{align*}) . Cas quatrième: 4k+3 +E(\frac{n+2}{4})+E(\frac{n+4}{4})&=E(\frac{4k+3-1}{2})+E(\frac{4k+3+2}{4})+E(\frac{4k+3+4}{4})\\&=E(2k+1)+E(k+\frac{5}{4})+E(k+\frac{7}{4})\\&=2k+1+k+E(\frac{5}{4})+k+E(\frac{7}{4})\\&=3k+1+1+k+1\\&=4k+3\\&=n\end{align*}) . Sauf erreur.
Dernière édition par nmo le Sam 29 Jan 2011, 19:07, édité 1 fois (Raison : Reprendre le message) | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 17:07 Sam 29 Jan 2011, 17:07 | |
| - nmo a écrit:
- Problème 53:
Soit ABCD un carré de côté 1.
Soient deux points M et N de (AB) et (BC) respectivement, de telle sorte que  . .
Calculez le périmètre du triangle MNB.
Bonne chance. Solution 53:Premiérement: ) =1-(\frac{MB*BN+BC(CN+AM)}{2}))  De l'autre coin, la formule de la surface dans un triangle affirme que: ) La formule d'ALkachi l'autre aussi, nous permet d'avoir: =\frac{MD^2+DN^2-MN^2}{2MD*DN}=\frac{2+AM^2+CN^2-(BM^2+BN^2)}{2MD*DN}) Or d'aprés les résultats précedants: }{2}}{\sqrt{2}}=\sqrt{2}(1-AM*CN)) la premiere équation (AM+BM)+(CN-BN)(CN+BN)}{2\sqrt{2}(1-AM*CN)}) (AB)+(CN-BN)(BC)}{2\sqrt{2}(1-AM*CN)}=\frac{2+AM-(1-AM)+CN-(1-BN)}{2\sqrt{2}(1-AM*CN)}) }) Donc 1-AM*CN=AM+CN. D'autre coté: MN^2=BN^2+CN^2 = (1-CN)^2+(1-AM)^2 <=> MN^2 = 2-2(CN+AM)+(AM+CN)^2-2AM*CN=(AM+CN)^2+2-2(1-CN*AM)-2AM*CN=(AM+CN)^2 Donc P_{MBN}=MN+BM+BN=(AM+CN)+(1-AM)+(1-CN)=2 ... CQFD.
Dernière édition par M.Marjani le Sam 29 Jan 2011, 20:27, édité 3 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 17:29 Sam 29 Jan 2011, 17:29 | |
|
Dernière édition par nmo le Sam 29 Jan 2011, 18:27, édité 2 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 17:39 Sam 29 Jan 2011, 17:39 | |
| - nmo a écrit:
- M.Marjani a écrit:
- La formule d'ALkachi nous permet d'avoir:
=\frac{MD^2+DN^2-MN^2}{2MD*DN}=\frac{2+AM^2-(BM^2+BN^2)}{2AM*CN}) . . A propos de cette ligne: tu as omis CN.
Puis comment, tu as MD.DN=AM.CN. C'est une faute d'innatention. Je vais édité méme les paragraphes, j'ai trouvé de petites errors d'innatetions. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 18:26 Sam 29 Jan 2011, 18:26 | |
| - nmo a écrit:
- Problème 53:
Soit ABCD un carré de côté 1.
Soient deux points M et N de (AB) et (BC) respectivement, de telle sorte que  . .
Calculez le périmètre du triangle MNB.
Bonne chance. Voici la solution: On pose tout d'abord:  et  . Et 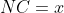 et 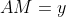 . On a d'un premier part: \bigg)}&\Leftrightarrow \tan{\frac{\pi}{4}}=\tan{\bigg(\frac{\pi}{2}-(\alpha+\beta)\bigg)}\\&\Rightarrow 1=\frac{1}{\tan{(\alpha+\beta)}}\\&\Rightarrow \tan{(\alpha+\beta)}=1\\&\Leftrightarrow \frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}.\tan{\beta}}=1\\&\Leftrightarrow \tan{\alpha}.\tan{\beta}=1-\tan{\alpha}.\tan{\beta}\\&\Leftrightarrow \frac{NC}{DC}+\frac{AM}{DC}=1-\frac{NC}{DC}.\frac{AM}{DC}\\&\Leftrightarrow \frac{x}{1}+\frac{y}{1}=1-\frac{x}{1}.\frac{y}{1}\\&\Leftrightarrow x+y=1-xy\end{align*}) . Et d'un deuxième, puisque le triangle MBN est rectangle et selon pytagore: ^2+(1-NC)^2\\&\Leftrightarrow MN^2=(1-x)^2+(1-y)^2\\&\Leftrightarrow MN^2=1-2x+x^2+1-2y+y^2\\&\Leftrightarrow MN^2=2-2(x+y)+x^2+y^2+2xy-2xy\\&\Leftrightarrow MN^2=2-2(1-xy)+(x+y)^2-2xy\\&\Leftrightarrow MN^2=2-2+2xy-2xy+(x+y)^2\\&\Leftrightarrow MN^2=(x+y)^2\\&\Leftrightarrow MN=x+y\end{align*}) . On calcule maintenat le périmètre p, celui du triangle BMN:  . Sauf erreur. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 19:22 Sam 29 Jan 2011, 19:22 | |
| - M.Marjani a écrit:
- La formule d'ALkachi l'autre aussi, nous permet d'avoir:
=\frac{MD^2+DN^2-MN^2}{2MD*DN}=\frac{2+AM^2-(BM^2+BN^2)}{2MD*DN}) Toujours, l'absence de NC vers la fin, il faut rectifier encore une fois. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 20:00 Sam 29 Jan 2011, 20:00 | |
| - nmo a écrit:
- M.Marjani a écrit:
- La formule d'ALkachi l'autre aussi, nous permet d'avoir:
=\frac{MD^2+DN^2-MN^2}{2MD*DN}=\frac{2+AM^2-(BM^2+BN^2)}{2MD*DN}) Toujours, l'absence de NC vers la fin, il faut rectifier encore une fois. Oeps ... Il m'a semblé qu'on cherche le périmétre de MDN xD.. Puisqu'il s'agissait de MBN donc le probléme se rend façile. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 20:10 Sam 29 Jan 2011, 20:10 | |
| - M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- La formule d'ALkachi l'autre aussi, nous permet d'avoir:
=\frac{MD^2+DN^2-MN^2}{2MD*DN}=\frac{2+AM^2-(BM^2+BN^2)}{2MD*DN}) Toujours, l'absence de NC vers la fin, il faut rectifier encore une fois. Oeps ... Il m'a semblé qu'on cherche le périmétre de MDN xD..
Puisqu'il s'agissait de MBN donc le probléme se rend façile. Je répète encore: tu as oublié CN et tu ne veux pas rectifier: cela m'enrage, prière de corriger. Tout ce que tu as fait est correct, même si tu as démontré plusieurs résultats iutiles. C'est bien, je vais chercher un exercice pour pouvoir continuer. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 20:48 Sam 29 Jan 2011, 20:48 | |
| - nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- La formule d'ALkachi l'autre aussi, nous permet d'avoir:
=\frac{MD^2+DN^2-MN^2}{2MD*DN}=\frac{2+AM^2-(BM^2+BN^2)}{2MD*DN}) Toujours, l'absence de NC vers la fin, il faut rectifier encore une fois. Oeps ... Il m'a semblé qu'on cherche le périmétre de MDN xD..
Puisqu'il s'agissait de MBN donc le probléme se rend façile. Je répète encore: tu as oublié CN et tu ne veux pas rectifier: cela m'enrage, prière de corriger.
Tout ce que tu as fait est correct, je te laisse continuer ta mission avant de continuer le jeu.
Vas-y, je t'attends! Je vois que tu parles de la faute de frappe? Elle ne pose aucun probleme dans la solution.. Elle s'est réctifier pour te calmer :d J'ai pas de bon probleme à proposer. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 21:57 Sam 29 Jan 2011, 21:57 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 29 Jan 2011, 22:09 Sam 29 Jan 2011, 22:09 | |
| Problème 55:Démontrez que le nombre  est un carré parfait. Bonne chance.P.S: cela fait deux heures de recherche pour pouvoir trouver cet exercice, amusez-vous bien. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 30 Jan 2011, 11:51 Dim 30 Jan 2011, 11:51 | |
|
Dernière édition par M.Marjani le Dim 30 Jan 2011, 13:25, édité 1 fois | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 30 Jan 2011, 12:59 Dim 30 Jan 2011, 12:59 | |
| - M.Marjani a écrit:
- Solution 55:
(10^{1997}+2)+9)=\frac{5^2}{3^2}(4.10^{1997}+4.10^{1997}+1)) tres bonne solution de ta part juste pour le carre vous avez oublié de le faire. amicalement  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 30 Jan 2011, 13:18 Dim 30 Jan 2011, 13:18 | |
| - yasserito a écrit:
- M.Marjani a écrit:
- Solution 55:
(10^{1997}+2)+9)=\frac{5^2}{3^2}(4.10^{2*1997}+4.10^{1997}+1))
tres bonne solution de ta part juste pour le carre vous avez oublié de le faire.
amicalement  Merçi. Generalisation: https://s281.photobucket.com/albums/kk213/MoKhTaR_Cs/?action=view¤t=solution.jpg | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 30 Jan 2011, 14:59 Dim 30 Jan 2011, 14:59 | |
|
Dernière édition par M.Marjani le Lun 31 Jan 2011, 17:08, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 31 Jan 2011, 16:59 Lun 31 Jan 2011, 16:59 | |
| Solution du problème 57 :f_4(x)-f_6(x)=1/4(cos^4(x)+sin^4(x))-1/6(cos^6(x)+sin^6(x)) =1/4(1-2cos²(x)sin²(x))-1/6(1-3cos²(x)sin²(x)) = 1/4-1/6 =1/12 CQFD  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 31 Jan 2011, 17:22 Lun 31 Jan 2011, 17:22 | |
| Solution du problème 56: cosx + sinx =V(1+2sinxcosx)=V(1+sin2x) Ainsi la fonction f(x)=V(x+1) vérifie l'énoncé f(tan²x)=V(1+tan²x)=V(1/cos²x)=1/cosx ( cosx >0) CQFD  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 31 Jan 2011, 17:55 Lun 31 Jan 2011, 17:55 | |
| @Mehdi.O: Les solutions que t'as proposé sont justes. Probléme 58: (**) ABC est un triangle. Prouver: (i) 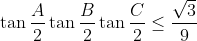 (ii) 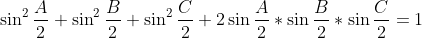 (iii) 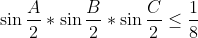 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
