| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 31 Jan 2011, 18:30 Lun 31 Jan 2011, 18:30 | |
| Il serait bien de changer un peu de trigonométrie, ces inégalités figurent au programme et leurs solutions sont présentes en DIMA DIMA, cela se ramène à faire des calculs qui sont ennuyeux.
Pour cela je postes un exercice plus compétitif :
Problème 59 : (***)
Dans un triangle ABC dont tous les angles sont aigus, la hauteur issue de C coupe (AB) en F et la médiane issue de B coupe (AC) en M.
Sachant que BM = CF et que <MBC =<FCA , montrer que ABC est un triangle équilatéral.
| |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 31 Jan 2011, 19:27 Lun 31 Jan 2011, 19:27 | |
|  Sauf erreur ^^ | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Fév 2011, 13:29 Mar 01 Fév 2011, 13:29 | |
| Bonjour Soumitous :
La première égalité est fausse Tu dois démontrer que <ABC=2<FCM car [BM] et la médiane non la bissectrice.
Ainsi cela enduit le reste en erreur | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Fév 2011, 13:32 Mar 01 Fév 2011, 13:32 | |
| Nous n'avons pas de bissectrice dans les données, juste une médiane et une hauteur.
Sinon l'exercice serait trivial, ainsi ta solution est fausse. | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Fév 2011, 13:45 Mar 01 Fév 2011, 13:45 | |
| j'ai cru que c'était une bissectrice désolé :S | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Fév 2011, 14:39 Mar 01 Fév 2011, 14:39 | |
| Solution au problème 59 : AFC est rectangle en F et M est le milieu de [AC], donc FM=MC, et par suite, FMC est isocèle en M. Par conséquent, MBC = MCF = MFC. Cela implique que le quadrilatère FMCB est inscriptible, et par suite, 90° = BFC = BMC. Ainsi, (BM) est également une hauteur, et est par conséquent une médiatrice. B appartient à la médiatrice, donc BC=AB, et donc le triangle est isocèle en B. Et d'après Pythagore sur BFC et BMC, on déduit que : FC² = BF² + BC² et MB² = MC² + BC², et puisque FC=MB, il vient BF=MC, et donc, BF=MC=FM. Si on note E le point d'intersection de FC et BM, alors cela implique que EFM = ECM et EMF=EBF, et puisque EBF=ECM car FMCB est inscriptible, alors EFM=EMF, et par conséquent, EFM est isocèle en E. Mais alors, d'après le théorème de Pythagore appliqué sur AFE et AEM, il vient AM=AF. On a montré que BF=MC et AF = AM. En sommant, on a comme voulu AB=AC, et par suite, ABC est équilatéral. Et que chacun se sente libre de proposer de nouveaux problèmes. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Fév 2011, 17:55 Mar 01 Fév 2011, 17:55 | |
| - Dijkschneier a écrit:
- Solution au problème 59 :

AFC est rectangle en F et M est le milieu de [AC], donc FM=MC, et par suite, FMC est isocèle en M. Par conséquent, MBC = MCF = MFC.
Cela implique que le quadrilatère FMCB est inscriptible, et par suite, 90° = BFC = BMC.
Ainsi, (BM) est également une hauteur, et est par conséquent une médiatrice.
B appartient à la médiatrice, donc BC=AB, et donc le triangle est isocèle en B.
Et d'après Pythagore sur BFC et BMC, on déduit que : FC² = BF² + BC² et MB² = MC² + BC², et puisque FC=MB, il vient BF=MC, et donc, BF=MC=FM.
Si on note E le point d'intersection de FC et BM, alors cela implique que EFM = ECM et EMF=EBF, et puisque EBF=ECM car FMCB est inscriptible, alors EFM=EMF, et par conséquent, EFM est isocèle en E.
Mais alors, d'après le théorème de Pythagore appliqué sur AFE et AEM, il vient AM=AF.
On a montré que BF=MC et AF = AM. En sommant, on a comme voulu AB=AC, et par suite, ABC est équilatéral.
Et que chacun se sente libre de proposer de nouveaux problèmes. Bien. Joli solution. - M.Marjani a écrit:
- Probléme 58: (**)
ABC est un triangle. Prouver:
(i) 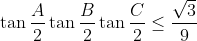
(ii)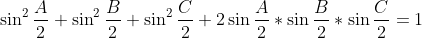
(iii) 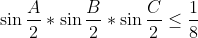 - Mehdi.O a écrit:
- Il serait bien de changer un peu de trigonométrie, ces inégalités figurent au programme et leurs solutions sont présentes en DIMA DIMA, cela se ramène à faire des calculs qui sont ennuyeux.
Parmi les questions que j'ai proposé n'existe qu'une figurant au manuel, par conséquant les autres sont un peu avancé et qui deviendront façiles que d'aprés une inspiration d'autres relations connus. Ils ne sont pas ennyeuses à ce degrés. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Fév 2011, 19:29 Mar 01 Fév 2011, 19:29 | |
| Je présente une autre solution au problème 59 : Dans le triangle ABM, nous avons sin (<ABM)/AM=sin(A)/Bm et sin(A)=FC/AC .Par conséquent : sin(<ABM)=(AM.FC)/(BM.AC)=1/2 => <ABM=30°. D'autre part sin(B)=FC/BC et sin(B)/AC=sin(A)/BC=BM/(2AM.AC)=> sin(B)=BM/AC=FC/AC donc AC=BC ainsi le triangle ABC est isocèle en C. Soit P l'intersection de (FC) et (BM) nous avons <BPF=60° donc <BPC=120°, et nous avons <ACF=<PCB=<MBC=<PBC donc PBC est isocèle en P ainsi <FCB=<MBC=30° . D'autre part puisque ABC est isocèle en C [CF] est hauteur et bissectrice de l'angle C, il s'ensuit que <ACB=60°. De ce fait ABC est équilatéral. CQFD  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 02 Fév 2011, 16:57 Mer 02 Fév 2011, 16:57 | |
| - Mehdi.O a écrit:
- Solution du problème 56:
cosx + sinx =V(1+2sinxcosx)=V(1+sin2x)
Ainsi la fonction f(x)=V(x+1) vérifie l'énoncé
f(tan²x)=V(1+tan²x)=V(1/cos²x)=1/cosx ( cosx >0)
CQFD  Je ne suis pas de ton avis, car 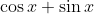 peut être négatif par contre 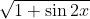 est toujours positif! A toi de rectifier. Cela veut dire que l'exercice 56 n'est pas encore résolu. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 02 Fév 2011, 17:53 Mer 02 Fév 2011, 17:53 | |
|
Dernière édition par yasserito le Jeu 03 Fév 2011, 22:57, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 02 Fév 2011, 23:51 Mer 02 Fév 2011, 23:51 | |
| - nmo a écrit:
- Mehdi.O a écrit:
- Solution du problème 56:
cosx + sinx =V(1+2sinxcosx)=V(1+sin2x)
Ainsi la fonction f(x)=V(x+1) vérifie l'énoncé
f(tan²x)=V(1+tan²x)=V(1/cos²x)=1/cosx ( cosx >0)
CQFD  Je ne suis pas de ton avis, car 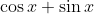 peut être négatif par contre peut être négatif par contre 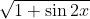 est toujours positif! est toujours positif!
A toi de rectifier.
Cela veut dire que l'exercice 56 n'est pas encore résolu. Je n'ai pas fais attention à la méthode qu'il a suivi, j'ai visé seulement le résultat. Il le manque des phrases et des phrases pour enfin déduire ce résultat (Surtout qu'il faut citer Cosx + Sinx >= 0 ). Donc voiçi une solution alternative:
En élevant le tout au carré: [f(sin(2x)]² = [sin(x) + cos(x)]² = sin²(x) + cos²(x) + 2cos(x)*sin(x) = 1 + sin(2x).
Notons maintenant que Sin(2x) est une fonction, qui a pour définition l'application de I vers l'intervalle [-1, 1], et qui réalise pour tout -1=<t=<1, [f(t)]² = 1+t, d'une cotée pour x de I, sin(x) + cos(x) >= 0 qui nous permet de dire donc f(t)=V(1+t) pour -1=<t=<1.
Maintenant, pour -Pi/4 =< x =< Pi/4, -1=<tan(x)=<1, et 0=<tan²(x)=<1. Alors que f(tan²(x))=V(1+tan²(x))=sec(x) | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 03 Fév 2011, 16:24 Jeu 03 Fév 2011, 16:24 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 04 Fév 2011, 11:39 Ven 04 Fév 2011, 11:39 | |
| - M.Marjani a écrit:
Je n'ai pas fais attention à la méthode qu'il a suivi, j'ai visé seulement le résultat. Il le manque des phrases et des phrases pour enfin déduire ce résultat (Surtout qu'il faut citer Cosx + Sinx >= 0 ). Donc voiçi une solution alternative:
En élevant le tout au carré: [f(sin(2x)]² = [sin(x) + cos(x)]² = sin²(x) + cos²(x) + 2cos(x)*sin(x) = 1 + sin(2x).
Notons maintenant que Sin(2x) est une fonction, qui a pour définition l'application de I vers l'intervalle [-1, 1], et qui réalise pour tout -1=<t=<1, [f(t)]² = 1+t, d'une cotée pour x de I, sin(x) + cos(x) >= 0 qui nous permet de dire donc f(t)=V(1+t) pour -1=<t=<1.
Maintenant, pour -Pi/4 =< x =< Pi/4, -1=<tan(x)=<1, et 0=<tan²(x)=<1. Alors que f(tan²(x))=V(1+tan²(x))=sec(x) Je pense que c'est encore faux, pour te convaicre la fonction 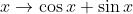 peut être négative. Mais puisque l'ensemble de définition de la fonction est \frac{-\pi}{4},\frac{\pi}{4}\big() , il vient que \frac{-\pi}{4},0\big(\bigg):\sin{x}+\cos{x}\le0) . Tu peux constater cela en représentant la fonction dans un repère orthonormé ou bien jeter un coup d'oeuil ici: http://www.wolframalpha.com/input/?i=%5Csin%7Bx%7D%2B%5Ccos%7Bx%7D. Cela veut dire que l'exercice 56 n'est pas encore résolu. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 04 Fév 2011, 14:44 Ven 04 Fév 2011, 14:44 | |
| - nmo a écrit:
- M.Marjani a écrit:
Je n'ai pas fais attention à la méthode qu'il a suivi, j'ai visé seulement le résultat. Il le manque des phrases et des phrases pour enfin déduire ce résultat (Surtout qu'il faut citer Cosx + Sinx >= 0 ). Donc voiçi une solution alternative:
En élevant le tout au carré: [f(sin(2x)]² = [sin(x) + cos(x)]² = sin²(x) + cos²(x) + 2cos(x)*sin(x) = 1 + sin(2x).
Notons maintenant que Sin(2x) est une fonction, qui a pour définition l'application de I vers l'intervalle [-1, 1], et qui réalise pour tout -1=<t=<1, [f(t)]² = 1+t, d'une cotée pour x de I, sin(x) + cos(x) >= 0 qui nous permet de dire donc f(t)=V(1+t) pour -1=<t=<1.
Maintenant, pour -Pi/4 =< x =< Pi/4, -1=<tan(x)=<1, et 0=<tan²(x)=<1. Alors que f(tan²(x))=V(1+tan²(x))=sec(x) Je pense que c'est encore faux, pour te convaicre la fonction 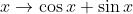 peut être négative. peut être négative.
Mais puisque l'ensemble de définition de la fonction est \frac{-\pi}{4},\frac{\pi}{4}\big() , il vient que , il vient que \frac{-\pi}{4},0\big(\bigg):\sin{x}+\cos{x}\le0) . .
Tu peux constater cela en représentant la fonction dans un repère orthonormé ou bien jeter un coup d'oeuil ici:
http://www.wolframalpha.com/input/?i=%5Csin%7Bx%7D%2B%5Ccos%7Bx%7D.
Cela veut dire que l'exercice 56 n'est pas encore résolu. Si l'intervalle de la définition de f est [-pi/4 , pi/4] c'est évident que -pi/4 =<x=< pi/4 <=> 0=<x+ pi/4=<pi/2 Donc cosx + sinx = V2*sin(x+pi/4) >=0 . C'est plutot l'inverse de ce que tu dis. N'oublie pas que la fonction sin(2x) est bijective de I vers l'intervalle [-1, 1].. il existe un unique x dans I tel que sin(2x)=t. Ainsi, pour -1=<t=<1, [f(t)]²=t+1. Pour x dans I, Sin(x)+Cos(x)>=0. Par conséquent f(t)=V(t+1) pour -1=<t=<1. S'il existe une autre solution pour ce probléme serait la bienvenue ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 09 Fév 2011, 17:33 Mer 09 Fév 2011, 17:33 | |
| - M.Marjani a écrit:
- Si l'intervalle de la définition de f est [-pi/4 , pi/4] c'est évident que -pi/4 =<x=< pi/4 <=> 0=<x+ pi/4=<pi/2
Donc cosx + sinx = V2*sin(x+pi/4) >=0 . C'est plutot l'inverse de ce que tu dis.
S'il existe une autre solution pour ce probléme serait la bienvenue ! C'est bien ce que tu dis. Désolé, lorsque j'était entrain de résoudre le problème, je n'ai pas fait très bien attention à la représentation graphique de notre fonction. Pour aller plus loin, on peut utiliser la dérivabilité. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 09 Fév 2011, 17:38 Mer 09 Fév 2011, 17:38 | |
| Les questions trigonométriques qu'a posées M.Marjani se traitent plutôt facilement après avoir remplacé les formes trigonométriques par leurs équivalents en fonction des côtés du triangle.
Puisque les calculs sont lourds, je ne vais pas y répondre, et proposer un nouveau problème.
Problème 60 : (* : une étoile)
Montrer que le produit de 4 entiers naturels consécutifs non nuls n'est jamais un carré parfait. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 09 Fév 2011, 19:29 Mer 09 Fév 2011, 19:29 | |
| (n-1)n(n+1)(n+2)=(n^3-n)(n+2)=n^4+2n^3-n²-2n=(n^2+n-1)²-1
et n^2+n-1#2 car apres delta on trouve des solution non appartenant a IN
et n^2+n-1#1 car n#0 et n#-2
alors le produit de 4entiers naturels consecutifs non nuls n'est jamais un carre parfait.
sauf erreur!
| |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 09 Fév 2011, 19:31 Mer 09 Fév 2011, 19:31 | |
| pour que la premiere ligne ait un sens n doit etre >=2 reste le cas de n=1
on trouve ainsi 1*2*3*4=24 qui n'est pas un carre parfait.
sauf erreur et merci! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 09 Fév 2011, 19:52 Mer 09 Fév 2011, 19:52 | |
| Problème 61 : (* : une étoile)
Sachant que x² + y² = 14x + 6y + 6, quelle est la plus grande valeur que peut prendre 3x+4y ? | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 09 Fév 2011, 22:22 Mer 09 Fév 2011, 22:22 | |
| (x-7)²+(y-3)²=64 alors selon C.S: 25[(x-7)²+(y-3)²]>=(3x+4y-33)²
on obtient alors 3x+4y-33<=40 alors 3x+4y<=73
alors la plus grande valeur que peut prendre 3x+4y est 73
sauf erreur et merci ! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 09 Fév 2011, 23:31 Mer 09 Fév 2011, 23:31 | |
| Bien. On peut aussi résoudre le problème par des considérations géométriques en voyant que (x-7)²+(y-3)²=64 est l'équation d'un cercle et 3x+4y=c l'équation d'une droite, et on cherche à maximiser c. Mais c est maximum lorsque la droite est tangente au cercle (pourquoi ?), i.e, lorsque la distance de la droite du centre du cercle vaut le rayon...
On peut aussi utiliser la méthode des multiplicateurs de Lagrange. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 09 Fév 2011, 23:37 Mer 09 Fév 2011, 23:37 | |
| oui vrm !bonne methode. et ca donne la meme valeur! | |
|
  | |
YIRA
Féru
 Nombre de messages : 33 Nombre de messages : 33
Age : 30
Date d'inscription : 13/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 10 Fév 2011, 21:43 Jeu 10 Fév 2011, 21:43 | |
|
Dernière édition par YIRA le Jeu 10 Fév 2011, 22:02, édité 1 fois | |
|
  | |
zouhir
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 33
Date d'inscription : 14/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 10 Fév 2011, 21:53 Jeu 10 Fév 2011, 21:53 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 10 Fév 2011, 22:08 Jeu 10 Fév 2011, 22:08 | |
| Problème 62 : (* : une étoile)
La suite f(n) définie sur IN vérifie la relation récurrente : 2[f(m+n) + f(m-n)] = f(2m) + f(2n), pour tous les entiers naturels m et n tels que m >= n, et aussi f(1)=1.
Déterminer f(1995). | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
