| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 26 Déc 2010, 14:04 Dim 26 Déc 2010, 14:04 | |
| Solution du problème 37 - Spoiler:
On a : 2^0 congru à 1 modulo 3 2 congru à 2 modulo 3 2^2 congru à 1 modulo 3 donc 2^n est soit congru à 2 soit à 1 modulo 3 donc 2^(2^n) est soit congru à 2^(4) soit congru à 2^(2) modulo 3 donc dans tout les cas 2^(2^n) est congru à 1 modulo 3 en ajoutant 5 on voit que ta somme est divisible par 3  Libre à vous de proposé Retfication : 0 est la seul solution .
Dernière édition par darkpseudo le Dim 26 Déc 2010, 17:04, édité 2 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 26 Déc 2010, 16:21 Dim 26 Déc 2010, 16:21 | |
| - Dijkschneier a écrit:
- Problème 37 : (** : deux étoiles)
Montrer que pour tout entier naturel n, 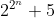 n'est jamais un nombre premier. n'est jamais un nombre premier.
Attention, les puissances sont en étage. Pour n=0, le nombre vaut 7, qui est bel et bien premier. A toi de rectifier. Je propose une réponse immédiatement, pour n entier non nul.
Dernière édition par nmo le Dim 26 Déc 2010, 16:41, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 26 Déc 2010, 16:40 Dim 26 Déc 2010, 16:40 | |
| - Dijkschneier a écrit:
- Problème 37 : (** : deux étoiles)
Montrer que pour tout entier naturel n, 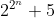 n'est jamais un nombre premier. n'est jamais un nombre premier.
Attention, les puissances sont en étage. J'admet que tu veux dire n appartient à l'ensemble des entier non nuls. Pour n=1, le nombre vaut 9. Pour n=2, le nombre vaut 21. Et ainsi de suite... On peut conjecturer que ce nombre est divisible par 3. Pour démontrer que 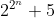 n'est jamais un nombre premier. Il suffit de démontrer que 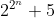 est divisible par 3 pour tout entier non nul. Procédons par récurrence: Pour n=1, le nombre vaut 9 qui est divisible par 3. Supposons que la propriété est vraie pour le rang n et démontrons qu'elle l'est aussi au rang n+1. Ainsi, il existe un k entier tel que 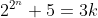 . Et prouvons l'existance d'un entier p, tel que 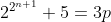 . On a 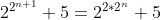 . Donc ^2+5) . Donc ^2+5) . Donc 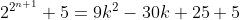 . Donc 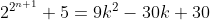 . Donc ) . Et en posant 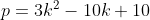 . Il vient que 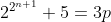 . Ainsi 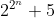 est divisible par 3 quelque soit n non nul. Et par suite 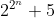 n'est jamais un nombre premier. CQFD. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 26 Déc 2010, 16:49 Dim 26 Déc 2010, 16:49 | |
| Problème 38:Dans le triangle ABC, la hauteur, la bissectrice, et la mediane issues du sommet A divisent l'angle 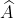 en quatres parties égales. Déterminez les amplitudes des trois angles du triangle. Bonne chance.P.S: J'attends une confirmation sur ma réponse précédante. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 01 Jan 2011, 12:20 Sam 01 Jan 2011, 12:20 | |
| - nmo a écrit:
- Problème 38:
Dans le triangle ABC, la hauteur, la bissectrice, et la mediane issues du sommet A divisent l'angle 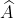 en quatres parties égales. en quatres parties égales.
Déterminez les amplitudes des trois angles du triangle.
Bonne chance.
P.S: J'attends une confirmation sur ma réponse précédante. Je propose la solution, et on passe à un nouvel exercice: Considérons le cercle T circonscrit au triangle ABC. La bissectrice [AE) de l'angle 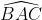 coupe le cercle circonscrit au triangle ABC au milieu I de l'arc BJC. La médiane [AM] comprend le milieu M de [BC]. I est le milieu de l'arc BJC et M est le milieu de la corde [BC] qui le sous tend. Dès lors IM est la médiatrice de cette corde [BC]. On sait que la droite (AD) est perpendiculaire à la droite (BC) (la hauteur) et la droite (IM) est perpendiculaire à la droite (BC) (la mediatrice) donc la droite (AD) est parallèle à la droite (MI). Les angles 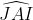 et 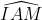 sont isométriques (alternes internes formés par des parallèles). Or les deux angles 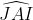 et 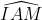 sont de même amplitude (l'hypothèse). Donc les angles 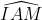 et 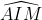 sont de même amplitude. Le triangle AMI est donc un triangle isocèle de sommet principal M et on a AM=MI. Le point M appartient donc à la médiatrice de [AI]. Le point M est commun aux médiatrices des cordes non parallèles [BC] et [AI] du cercle T. M est donc le centre de ce cercle et l'angle 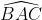 est donc un angle de 90° (inscrit dans un demi cercle). Le triangle CMA est aussi un triangle isocèle puisque MA=MC (rayons). Dès lors, les angles 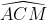 et 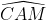 ont même mesure qui vaut 90°/4 soit 22.5°. Et l'angle 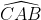 a pour mesure 90°-22.5° soit 67.5°. P.S: cette solution, ainsi que le problème figure dans une revue belge nommée "losanges". | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 01 Jan 2011, 12:57 Sam 01 Jan 2011, 12:57 | |
| Exercice 39:Soit x, y, et z trois réels strictement supérieurs à 1, tel que 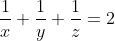 . Démontrez que 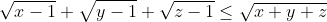 . Exercice 40:Soit s et t les racines de l'équation 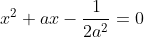 . Démontrez que 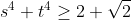 . Bonne chance. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 02 Jan 2011, 20:50 Dim 02 Jan 2011, 20:50 | |
| - M.Marjani a écrit:
- Solution 36:
Bienvu : 0=<1-y=<1 <=> 0=<y=<1 (A). Donc P(x,y): f(x+y)>=f(x)+f(y) => P(1-y,y): 1>=f(y)+f(1-y) (C).
Selon (C): f(x)=<1-f(1-x). On suppose que f(x)>2x (1) , donc 2x<f(x)=<1-f(1-x) donc f(1-x)<1-2x
On pose 1-x=X avec X£[0,1] selon (A), donc f(x)<1-2(1-x) ==> f(x)<2x-1 ==> contradiction avec notre supposition (1). D'ou f(x)=<2x.
Réciproquement: 2(x+y)>=f(x+y)>=f(x)+f(y). Or 2(x+y)=2x+2y>=f(x)+f(y) ce qui est juste.
CQFD. - Dijkschneier a écrit:
- Tu as f(x)>2x et f(x)<2x-1, mais il n'y a pas de contradiction, puisque ce n'est pas le même x...
J'ai l'impression que tu cherches à rendre correcte une démonstration qui ne l'est pas... Il s'agit d'une question de fonctions non pas de variables. Les variables que j'ai utilisé sont du méme intervalle [0,1] J'ai l'impression que ma derniére solution est juste sauf autre faute. Solution 39:- Spoiler:
 tel que (a,b,c)>0. }) Par Cauchy swhartz: }) \geq%201+1+1) (\frac{1}{x}+\frac{1}{y}+\frac{1}{z})=1+1+1+(\frac{x}{y}+\frac{y}{x})+(\frac{x}{z}+\frac{z}{x})+(\frac{y}{z}+\frac{z}{y})\geq%209) Donc x+y+z>=9/ Donc x+y+z>=9/2 +(y-1)+(z-1)=a^2+b^2+c^2}) D'ou le résultat. - Spoiler:
On a s et t les raçines de l'equation 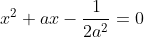 alors (x-t)=x^2+ax-\frac{1}{2a^2}\Leftrightarrow%20x^2-x(s+t)+st=x^2+ax-\frac{1}{2a^2}) Alors  . On sait que: ^4=(s^2+2st+t^2)^2=s^4+t^4-2st(2(s+t)^2-st)\Leftrightarrow%20s^4+t^4=(s+t)^4+2st(2(s+t)^2-st)) +2) et d'aprés IAG: =a^4+\frac{1}{2a^4}\geq%20\sqrt{2}) D'ou le résultat.
PS: J'attend une confirmation pour proposé. : )
Dernière édition par M.Marjani le Dim 02 Jan 2011, 21:44, édité 2 fois | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 02 Jan 2011, 21:39 Dim 02 Jan 2011, 21:39 | |
| svp j'ai pas bien compris M.marjani est ce -1/2a² ou 1/2a² ? car au premier t'as fait - et apres tas fait + . svp peut etre c'est ma faute mais j'espere bien y savoir!! et merci | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 02 Jan 2011, 21:40 Dim 02 Jan 2011, 21:40 | |
| - yasserito a écrit:
- svp j'ai pas bien compris M.marjani est ce -1/2a² ou 1/2a² ? car au premier t'as fait - et apres tas fait + . svp peut etre c'est ma faute mais j'espere bien y savoir!! et merci
Qu'une faute de frappe editée. : ) J'attend nmo pour proposer. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 03 Jan 2011, 17:46 Lun 03 Jan 2011, 17:46 | |
| - M.Marjani a écrit:
- Solution 40:
On a s et t les raçines de l'equation 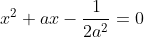
alors (x-t)=x^2+ax-\frac{1}{2a^2}\Leftrightarrow%20x^2-x(s+t)+st=x^2+ax-\frac{1}{2a^2})
Alors  . On sait que: . On sait que:
^4=(s^2+2st+t^2)^2=s^4+t^4-2st(2(s+t)^2-st)\Leftrightarrow%20s^4+t^4=(s+t)^4+2st(2(s+t)^2-st))
+2) et d'aprés IAG: et d'aprés IAG: =a^4+\frac{1}{2a^4}\geq%20\sqrt{2})
D'ou le résultat. Je pense que tu as commis une faute en voulant simplifier, le signe négatif doit être positif. En effet, on a ^4=s^4+t^4+2st(2(s+t)^2-st)) . Cependant, le résultat est correct. Pour l'autre exercice, il est correct. Et je vais proposer une solution alternative, sans changement de variable. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 03 Jan 2011, 17:58 Lun 03 Jan 2011, 17:58 | |
| - nmo a écrit:
- Exercice 39:
Soit x, y, et z trois réels strictement supérieurs à 1, tel que 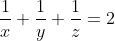 . .
Démontrez que 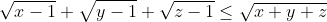 . . Voici une autre solution: On a 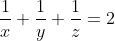 . Donc 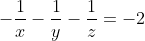 . Donc 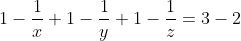 . Donc 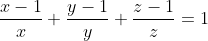 . Or, on a \big(\frac{x-1}{x}+\frac{y-1}{y}+\frac{z-1}{z}\big)}\ge\sqrt{\frac{(x-1)}{x}*x}+\sqrt{\frac{y-1}{y}*y}+\sqrt{\frac{z-1}{z}*z}) . (Selon l'inégalité de Caushy Schwartz). Il en résulte que 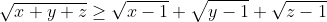 . CQFD. P.S: J'aime bien dire que pour l'autre exercice, on utilise l'inégalité arithmético-géométrique directement. On a en effet,  . Avec 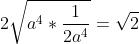 . Au plaisir. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 03 Jan 2011, 18:26 Lun 03 Jan 2011, 18:26 | |
| Exercice 41:Résolvez en IR² le système suivant: \begin{cases}(x-1)(y^2+6)=y(x^2+1)\\(y-1)(x^2+6)=x(y^2+1)\end{cases}) . Bonne chance.P.S: Je ne sais pas si c'est abordable par un élève du niveau première année du cycle du baccalauréat sciences mathématiques, c'est le seul que je trouve à présent. J'essayerai personnellement plus tard, car je n'ai pas de temps maintenant. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 03 Jan 2011, 19:43 Lun 03 Jan 2011, 19:43 | |
| J'ai remarqué que ça faciliterai la tache si on passais par cosh et sinh ( respectivement cos hyperbolique et sin hyperbolique ) mais je n'essai même pas vu que ce n'est pas de votre niveau . En attente d'une solution plus abordable . | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 03 Jan 2011, 23:46 Lun 03 Jan 2011, 23:46 | |
| - darkpseudo a écrit:
- J'ai remarqué que ça faciliterai la tache si on passais par cosh et sinh ( respectivement cos hyperbolique et sin hyperbolique ) mais je n'essai même pas vu que ce n'est pas de votre niveau . En attente d'une solution plus abordable .
C'est directe.. : ) Puisque le systéme{xy²+6x-y²-6=yx²+y (1) ET x²y+6y-x²-6=xy²+x (2)} a deux inconus, alors il suffit de constuire deux équation à partir de çe dernier, de préferable la somme et la différence:
La différence de (1) et (2) donne: -2xy(x-y)+7(x-y)+(x-y)(x+y)=0 donc x=y Ou x+y=2xy-7 (C)
Ce qui nous pousse de faire la somme de (1) et (2): -(x+y)²+5(x+y)+2xy-12=0 ==> (A)
1ér Cas: x=y: Et de remplaçer dans (A), -4x²+10x+2x²-12=0 alors x²-5x+6=0 , Delta=1 donc x=y=2 ou x=y=3
Le premier systéme se réduit en une seule équation: x²-5x+6=0 donc S_1={(2,2);(3,3)}
2éme Cas: x+y=2xy-7: (2xy-7)²-5(2xy-7)-2xy+12=0 <=> 4(xy)²-28xy+49-12xy+35+12=0 <=> (xy)²-10xy+24=0
Delta=4 ==> xy=6 alors d'aprés (C) x+y=5 donc x²-5x+6=0.. Ou xy=4 <=> x+y=1 donc x²-x+4=0 impossible car x²-x+1>0. S={(2,2);(3,3);(2,3);(3,2)} En haut un peu.. : ) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 05 Jan 2011, 15:48 Mer 05 Jan 2011, 15:48 | |
| - M.Marjani a écrit:
- darkpseudo a écrit:
- J'ai remarqué que ça faciliterai la tache si on passais par cosh et sinh ( respectivement cos hyperbolique et sin hyperbolique ) mais je n'essai même pas vu que ce n'est pas de votre niveau . En attente d'une solution plus abordable .
C'est directe.. : )
Puisque le systéme{xy²+6x-y²-6=yx²+y (1) ET x²y+6y-x²-6=xy²+x (2)} a deux inconus, alors il suffit de constuire deux équation à partir de çe dernier, de préferable la somme et la différence:
La différence de (1) et (2) donne: -2xy(x-y)+7(x-y)+(x-y)(x+y)=0 donc x=y Ou x+y=2xy-7 (C)
Ce qui nous pousse de faire la somme de (1) et (2): -(x+y)²+5(x+y)+2xy-12=0 ==> (A)
1ér Cas: x=y: Et de remplaçer dans (A), -4x²+10x+2x²-12=0 alors x²-5x+6=0 , Delta=1 donc x=y=2 ou x=y=3
Le premier systéme se réduit en une seule équation: x²-5x+6=0 donc S_1={(2,2);(3,3)}
2éme Cas: x+y=2xy-7: (2xy-7)²-5(2xy-7)-2xy+12=0 <=> 4(xy)²-28xy+49-12xy+35+12=0 <=> (xy)²-10xy+24=0
Delta=4 ==> xy=6 alors d'aprés (C) x+y=5 donc x²-5x+6=0.. Ou xy=4 <=> x+y=1 donc x²-x+4=0 impossible car x²-x+1>0. S={(2,2);(3,3);(2,3);(3,2)} Bien. Je propose un autre exercice si je le trouve, sinon tu peux proposer le tien. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 05 Jan 2011, 17:01 Mer 05 Jan 2011, 17:01 | |
| Exercice 42:Résolvez en IR l'équation suivante: ^{\frac{1}{4}}+(x)^{\frac{1}{4}}=5) . Exercice 43:ABCD est un rectangle, et M un point non situé sur (AB). Soient: -C' le projeté orthogonal de C sur (AM) -D' le projeté orthogonal de D sur (BM) -M' le projeté orthogonal de M sur (AB) Montrez que les droites (MM'), (CC'), et (DD') sont concourantes. Bonne chance. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 09 Jan 2011, 14:23 Dim 09 Jan 2011, 14:23 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 10 Jan 2011, 17:02 Lun 10 Jan 2011, 17:02 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 12 Jan 2011, 16:13 Mer 12 Jan 2011, 16:13 | |
| - nmo a écrit:
- Exercice 43:
ABCD est un rectangle, et M un point non situé sur (AB).
Soient:
-C' le projeté orthogonal de C sur (AM)
-D' le projeté orthogonal de D sur (BM)
-M' le projeté orthogonal de M sur (AB)
Montrez que les droites (MM'), (CC'), et (DD') sont concourantes.
Bonne chance. Voici une solution qui requiert les connaissances de l'année précédante: Soit t la translation de vecteur 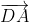 . On a ABCD un paralléllogramme. Donc 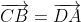 . Donc t(C)=B. Et l'image de (CC') par t est la doite parallèle à (CC') passant par B. Elle est perpendiculaire à (AM): c'est donc la hauteur de AMB issue de B.==>(1) De plus, on a (AD) est perpendiculaire à (AB) et (MM') est perpendiculaire à (AB). Donc (AD) est parallèle à (MM)'. L'image de (MM') par t est donc (MM'): la hauteur de AMB issue de M.==>(2) On a enfin t(D)=A. Et l'image de (DD') par t est la doite parallèle à (DD') passant par A. Elle est perpendiculaire à (MB): c'est donc la hauteur de AMB issue de A.==>(3) De 1, 2, et 3, on conclut que les images par t des droites (MM'), (CC'), et (DD') sont donc les trois hauteurs du triangle AMB. Ces images étant concourante en un un point, leurs antécédants sont par conséquent également concourantes en un point. Ce qui met fin à la démonstration. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 12 Jan 2011, 16:40 Mer 12 Jan 2011, 16:40 | |
| Exercice 44:Démontrez que 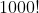 est divisible par 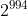 . Trouvez le plus grand entier tel que 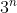 divise 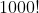 . Bonne chance.
Dernière édition par nmo le Mer 12 Jan 2011, 17:27, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 12 Jan 2011, 17:07 Mer 12 Jan 2011, 17:07 | |
| Solution au problème 44 :1) 1000! est clairement un multiple de 94.2^9 car 94 et 2^9=512 sont deux entiers différents et inférieurs à 1000 : 1000! = 1.2.3...94...512...999.1000 2) Selon la formule de Legendre : %20&=%20E(\frac{1000}{3})+E(\frac{1000}{9})+E(\frac{1000}{27})+E(\frac{1000}{81})+E(\frac{1000}{243})+E(\frac{1000}{729})%20\\%20&=%20333%20+%20111%20+%2037%20+%2012%20+%204%20+%201%20\\%20&=%20498%20\end{align*}) Le plus grand n vérifiant 3^n divise 1000! est par conséquent 498. Et je n'ai pas de problème à proposer pour le moment. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 12 Jan 2011, 17:28 Mer 12 Jan 2011, 17:28 | |
| - Dijkschneier a écrit:
- Solution au problème 44 :
1) 1000! est clairement un multiple de 94.2^9 car 94 et 2^9=512 sont deux entiers différents et inférieurs à 1000 : 1000! = 1.2.3...94...512...999.1000 Désolé, j'ai commis une terrible faute de frappe. C'est éditée. Ta solution pour le deuxième est utile pour résoudre le premier aussi. A l'aide de la formule que tu as annoncée, il devient trivial. Personellement, j'ai proposé l'exercice car je ne savais pas cette formule de Legendre. Je vais chercher un nouvel exercice. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 12 Jan 2011, 18:05 Mer 12 Jan 2011, 18:05 | |
| Exercice 45:Soit ABC un triangle tel que AB=n, AC=n+1, et BC=n+2. Trouvez les amplitudes des angles de ce triangle sachant que l'angle 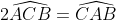 . Bonne chance.
Dernière édition par nmo le Sam 15 Jan 2011, 18:56, édité 1 fois | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 12 Jan 2011, 21:17 Mer 12 Jan 2011, 21:17 | |
| selon la loi des sinus on a : sin(c)/n=sin(2c)/(n+2)=sin(TT-3c)/(n+1)
alors sin(2c)/sin(c)=(n+2)/n et sin(3c)/sin(c)=(n+1)/n
alors 2cos(c)=(n+2)/n et [sin(2c)cos(c)+sin(c)cos(2c)]/sin(c)=(n+1)/n
alors 4cos²(a)=(n+2)²/n² et (4cos²(a)-1)=(n+1)/n
alors 4cos²(a)=(n+2)²/n² et 4cos²(a)=(2n+1)/n
alors (n+2)²=n(2n+1) alors n²-3n-4=0 alors n=4 ou n=-1
alors n=4 ca veut dire 2cos(c)=3/2 alors cos(c)=3/4
alors c=41.4 et a=62.8 et b=75.8
sauf erreur et merci
Dernière édition par yasserito le Sam 15 Jan 2011, 19:33, édité 2 fois | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 12 Jan 2011, 21:22 Mer 12 Jan 2011, 21:22 | |
|
Dernière édition par yasserito le Sam 15 Jan 2011, 19:36, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
